§ 5. Комплексные числа

1. Возникновение комплексных чисел

По ряду причин возникла потребность в расширении понятия числа даже за пределы континуума действительных чисел - посредством введения так называемых комплексных чисел. Необходимо ясно представлять себе, что все подобного рода расширения и нововведения приходят отнюдь не в результате чьих-то индивидуальных усилий. Скорее их можно рассматривать как итог некоторой постепенной и исполненной колебаний эволюции, в которой не должна быть преувеличиваема роль отдельных личностей. Одной из причин, которые обусловили появление и употребление отрицательных и дробных чисел, было стремление к большей свободе в формальных вычислениях. Только к концу средневековья математики стали терять ощущение беспокойства и неуверенности, с которым они оперировали этими понятиями, тогда как ничего подобного не наблюдалось в отношении таких интуитивно ясных и конкретно воспринимаемых понятий, как понятие натурального числа.

Простейшая процедура, требующая применения комплексных чисел, есть решение квадратных уравнений. Напомним, как обстояло дело с линейным уравнением ах = b, когда нужно было определить удовлетворяющее ему значение неизвестной величины x. Решение имеет вид 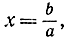и введение дробных чисел как раз обусловливается требованием, чтобы всякое линейное уравнение с целыми коэффициентами (при а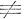0) было разрешимо. Уравнения вроде

не имеют решения в области рациональных чисел, но имеют таковое в расширенном поле всех действительных чисел. Но даже действительных чисел недостаточно обширно, чтобы в нем можно было построить полную и законченную теорию квадратных уравнений. Например, следующее очень простое уравнение

не имеет действительных решений, так как квадрат действительного числа никак не может быть отрицательным.

Нам приходится или удовольствоваться тем положением, что такие простые уравнения неразрешимы, или следовать по уже знакомому пути - расширять числовую область и вводить новые числа, с помощью которых удастся решить уравнение. Именно это самое и делается, когда вводят новый символ i и принимают, в качестве определения, что i² = -1. Разумеется, этот объект - "мнимая единица" - не имеет ничего общего с числом как орудием счета. Это - отвлеченный символ, подчиненный основному закону i² = -1, и ценность его зависит исключительно от того, будет ли достигнуто в результате его введения действительно полезное расширение числовой системы.

Так как мы хотим складывать и умножать с помощью символа i так же, как с обыкновенными числами, то естественно пользоваться символами вроде 2i, 3i, -i, 2+5i, вообще, a+bi, где а и b - действительные числа. Раз эти символы должны подчиняться коммутативному, ассоциативному и дистрибутивному законам, то должны быть возможны, например, такие вычисления:

Руководствуясь этими соображениями, мы начинаем систематическое изложение теории комплексных чисел со следующего определения: символ вида а + bi, где а и b - два действительных числа, носит название комплексного числа с действительной частью а и мнимой частью b. Операции сложения и умножения совершаются над этими числами так, как будто бы i было обыкновенное действительное число, однако с условием заменять i² через -1. Точнее говоря, сложение и умножение определяются по формулам:

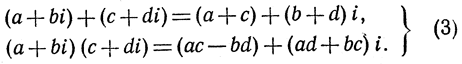
В частности, мы получаем:

Основываясь на этих определениях, легко проверить, что для комплексных чисел справедливы коммутативный, ассоциативный и дистрибутивный законы. Далее, не только сложение и умножение, но также и вычитание и деление, будучи применены к двум комплексным числам, приводят снова к комплексным числам того же вида а + bi, так что комплексные числа образуют поле (см. стр. 81):

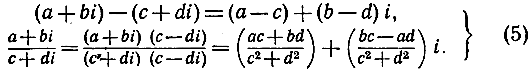
(Второе равенство теряет смысл, если с + di = 0 + 0i, так как тогда с² + d² = 0. Значит, и на этот раз нужно исключить деление на нуль, т. е. на 0 + 0i.) Например,

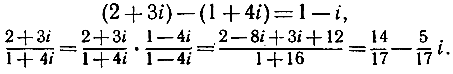
Поле комплексных чисел включает поле действительных чисел в качестве "подполя", так как комплексное число а + 0i отождествляется с действительным числом а. Заметим, с другой стороны, что комплексное число вида 0 + bi = bi называется "чисто мнимым".

Упражнения. 1) Представить 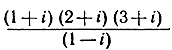в форме а + bi.

2) Представить 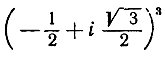в форме а + bi.

3) Представить в форме а + bi следующие выражения:

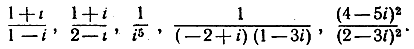
4) Вычислить 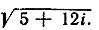(Указание. Напишите 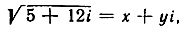, возведите в квадрат и сравняйте действительные части и мнимые части.)

Вводя символ i, мы расширили поле действительных чисел и получили поле символов а + bi, в котором квадратное уравнение

имеет два решения: х = i и х = -i. В самом деле, согласно определению i*i = (-i)(-i) = i² = -1. Нужно сказать, что мы приобрели гораздо больше: можно легко проверить, что теперь каждое квадратное уравнение

становится разрешимым. В самом деле, выполняя над равенством (6) ряд преобразований, мы получаем:

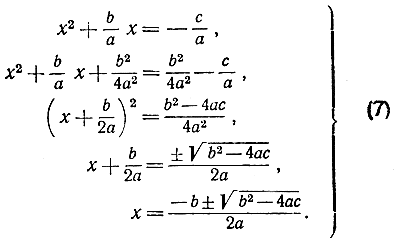
Заметим теперь, что если b²-4ac, то 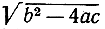есть обыкновенное действительное число и корни уравнения (7) действительные; если же b²-4ас<0, то тогда 4ас-b²>0, и следовательно, 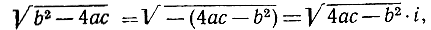так что уравнение (7) имеет в качестве корней мнимые числа. Так, например, уравнение

имеет действительные корни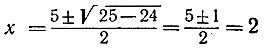

или 3, тогда как уравнение

имеет мнимые корни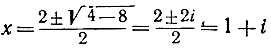

или 1-i.