2. Уравнения прямых и кривых линий

Если С есть неподвижная точка с координатами х = а, у = b, то геометрическое место всех точек Р, находящихся от точки С на данном расстоянии r, есть окружность с центром С и радиусом r. Из формулы для расстояния между двумя точками (1) следует, что точки этой окружности имеют координаты х, у, удовлетворяющие уравнению

Это уравнение называется уравнением окружности, так как оно выражает полное (необходимое и достаточное) условие того, это точка Р с координатами х, у лежит на окружности с центром С и радиусом r. Если раскрыть скобки, уравнение принимает вид

где k = r² - а² - b². Обратно, если задано уравнение вида (3), причем a, b и k - произвольные постоянные и сумма k + a² + b² положительна, то с помощью алгебраической процедуры "дополнения до квадрата" мы можем написать, то же уравнение в форме

где r² = k + а² + b². Теперь ясно, что уравнение (3) определяет окружность радиуса r, центр которой - в точке С с координатами а, b.

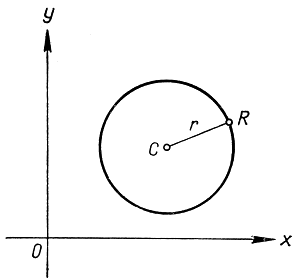
Рис. 15. Окружность

Уравнение прямой еще проще по своей форме. Так, например, уравнение оси х имеет вид у = 0, так как координата у равна нулю для всех точек этой оси и ни для каких иных точек. Точно так же ось у имеет уравнение х = 0. Прямые, проходящие через начало и делящие пополам углы между осями, имеют уравнения х = у и х = -у. Легко показать, что всякая прямая линия имеет уравнение вида

где а, b, с - постоянные, характеризующие эту прямую. Как и в других случаях, смысл уравнения (4) - тот, что пары действительных чисел х, у, удовлетворяющих этому уравнению, являются координатами некоторой точки на прямой, и обратно.

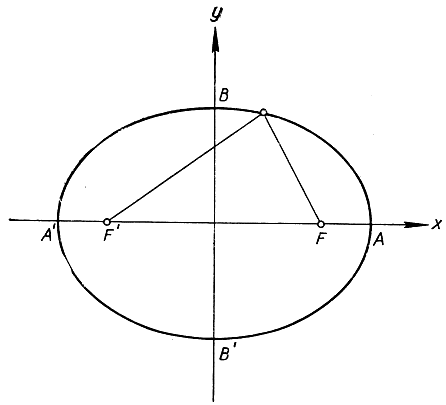
Рис. 16. Эллипс с фокусами

Может быть, читатель учил в школе, что уравнение вида

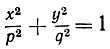
представляет эллипс (рис. 16). Эта кривая пересекает ось х в точках А (р, 0) и А' (-р, 0) и ось у - в точках В (0, q) и В'(0, -q). (Обозначение Р (х, y), или, еще короче, (х, y), вводится ради кратности и должно быть расшифровано так: "точка Р с координатами х и y".) Если p>q, то отрезок АА' длины 2р называется большой осью эллипса, а отрезок ВВ' длины 2q - его малой осью. Эллипс есть геометрическое место точек Р, сумма расстояний которых от точек 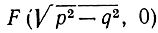и 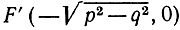равна 2р. Читатель сможет проверить это в качестве упражнения, применяя формулу (1). Точки F и F' называются фокусами эллипса, а отношение 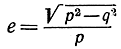называется его эксцентриситетом. Уравнение вида

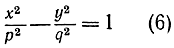
представляет гиперболу. Эта кривая состоит из двух ветвей, пересекающих ось х соответственно в точках А (р, 0) и А'(-р, 0) (рис. 17). Отрезок АА' длины 2р называется "действительной" осью гиперболы. Гипербола, удаляясь в бесконечность, приближается к двум прямым qx ± py = 0, но так с ними и не пересекается; эти прямые называются асимптотами гиперболы. Гипербола есть геометрическое место точек Р, разность расстояний которых до двух точек 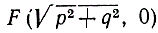и 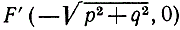по абсолютной величине равна 2р. Эти точки в случае гиперболы тоже называются фокусами; под эксцентриситетом гиперболы понимают отношение .

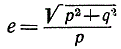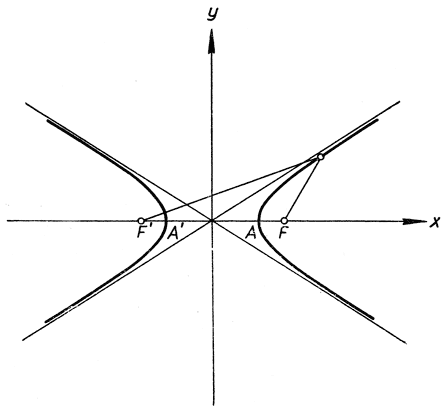
Рис. 17. Гипербола с фокусами

Уравнение

также определяет гиперболу, но такую, для которой асимптотами являются две оси (рис. 18). Уравнение этой "равносторонней" гиперболы геометрически означает, что площадь прямоугольника OP'PQ' (см. рис. 12), связанного с точкой Р, для всякой точки Р кривой равна 1. Равносторонняя гипербола несколько более общего вида

где с - постоянная, представляет собой частный случай гиперболы в том же смысле, в каком окружность представляет собой частный случай эллипса. Отличительная характеристика равносторонней гиперболы заключается в том, что ее две асимптоты (в нашем случае - две оси) взаимно перпендикулярны.

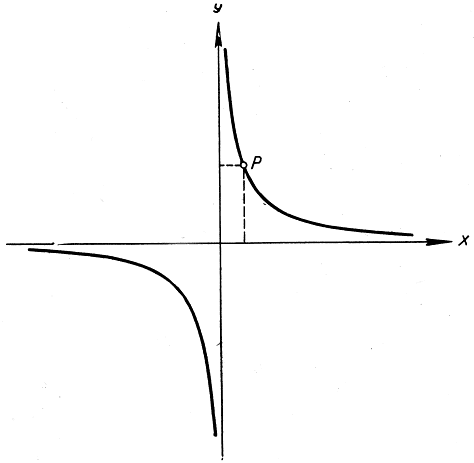
Рис. 18. Равносторонняя гипербола. Площадь прямоугольника, определенного точкой Р (х, у), равна 1

Во всем этом для нас самым интересным является руководящая идея: геометрические объекты могут полностью описываться в арифметической или алгебраической форме. То же справедливо и относительно геометрических операций. Например, если нам требуется найти точки пересечения двух прямых, то мы рассматриваем их два уравнения

и для нахождения общей точки этих двух прямых достаточно решить систему (8); решение дает нам координаты искомой точки. Таким же образом точки пересечения двух произвольных кривых (скажем, окружности х² + у² - 2ах - 2by = k и прямой ах + by = с) находятся посредством совместного решения их уравнений.