§ 4. Математический анализ бесконечного

1. Основные понятия

Последовательность натуральных чисел

представляет собой первый и самый важный пример бесконечного множества. Не нужно видеть ничего таинственного в том, что она - бесконечная, что у нее "нет конца": как бы велико ни было натуральное число n, можно построить другое, следующее за ним число, еще большее - n+1. Но при переходе от прилагательного "бесконечный", означающего просто-напросто "не имеющий конца", к существительному "бесконечность" никоим образом не следует привносить допущения, что "бесконечность", обыкновенно изображаемая особым символом ∞, может быть рассматриваема как обыкновенное число. Нельзя включить символ ∞ в числовую систему действительных чисел, не нарушая при этом основных законов арифметики. И тем не менее идея бесконечности пронизывает всю математику, так как математические объекты изучаются обыкновенно не как индивидуумы - каждый в отдельности, а как члены классов или совокупностей, содержащих бесчисленное множество элементов одного и того же типа; таковы совокупности натуральных чисел, действительных чисел или же треугольников на плоскости. Именно по этой причине возникает необходимость в точном математическом анализе бесконечного. Современная теория множеств, созданная Георгом Кантором и его школой в конце XIX столетия, приступив к разрешению этой задачи, достигла значительных успехов. Канторова теория множеств глубоко проникла во многие области математики и оказала на них огромное влияние; она стала играть особо выдающуюся роль в исследованиях, связанных с логическим и философским обоснованием математики. Исходным в канторовой теории является общее понятие совокупности, или множества. При этом имеется в виду собрание объектов (элементов), которое определяется некоторым правилом, позволяющим с полной определенностью судить о том, входит ли данный объект в число элементов собрания или не входит. Примерами могут служить множество всех натуральных чисел, множество всех периодических десятичных дробей, множество всех действительных чисел или множество всех прямых в трехмерном пространстве.

Для того чтобы сравнивать множества с точки зрения "количества" содержащихся в них элементов, нужно ввести основное в этой теории понятие "эквивалентности" множеств. Если элементы двух множеств А и В могут быть приведены в попарное соответствие такого рода, что каждому элементу множества А сопоставлен один и только один элемент множества В, а каждому элементу множества В сопоставлен один и только один элемент множества А, то установленное таким образом соответствие называется взаимно однозначным, а о самих множествах А и В тогда говорят, что они между собой эквивалентны. Понятие эквивалентности в случае конечных множеств совпадает с обыкновенным понятием числового равенства, так как два конечных множества в том и только в том случае могут быть приведены во взаимно однозначное соответствие, если содержат одно и то же число элементов. На этом и основывается, нужно заметить, идея счета, когда мы "считаем" элементы множества, то процесс счета как раз и заключается в установлении взаимно однозначного соответствия между элементами множества и числами 1, 2, ..., n.

Чтобы установить эквивалентность двух конечных множеств, иногда нет необходимости "считать" элементы. Так, например, не считая, можно утверждать, что конечное множество кругов единичного радиуса эквивалентно множеству их центров.

Перенося понятие эквивалентности на бесконечные множества, Кантор имел в виду создать "арифметику" бесконечного. Множество действительных чисел и множество точек на прямой линии - эквивалентны, так как после того, как выбраны начало и единичный отрезок, данная прямая становится "числовой прямой", и каждой ее точке Р в качестве координаты взаимно однозначно сопоставляется некоторое совершенно определенное действительное число х:

Четные числа образуют правильное подмножество множества всех натуральных чисел, а все целые числа образуют истинное подмножество множества всех рациональных чисел. (Говоря о "правильном" подмножестве некоторого множества S, мы имеем в виду такое множество S', которое состоит из элементов множества S, но не из всех его элементов.) Совершенно ясно, что если данное множество конечно, т. е. содержит какое-то число n элементов, и не более того, то оно не может быть эквивалентно никакому своему правильному подмножеству, так как всякое правильное его подмножество содержало бы самое большее n-1 элементов. Но если данное множество содержит бесконечное число элементов, то, как это ни парадоксально, оно может быть эквивалентно некоторому своему истинному подмножеству. Например, схема

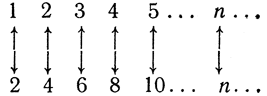
устанавливает взаимно однозначное соответствие между множеством натуральных чисел и множеством всех четных целых положительных чисел, и эти два множества оказываются эквивалентными, хотя второе есть истинное подмножество первого. Такое противоречие с ходячей истиной "целое больше своей части" показывает, какие сюрпризы нас ждут в области "арифметики бесконечного".