1. Основной принцип

Уже начиная с XVII в. числовой континуум, принимаемый как нечто само собой разумеющееся или же подвергаемый более или менее поверхностному критическому анализу, стал основой математики, в частности аналитической геометрии и дифференциального и интегрального исчислений.

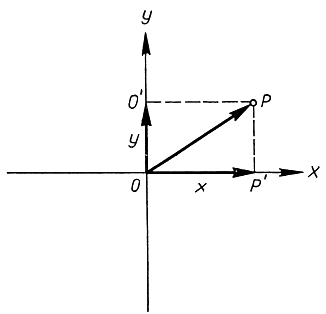
Рис. 12. Прямоугольные координаты точки

Введение числового континуума дает возможность сопоставить каждому отрезку прямой в качестве его "длины" некоторое определенное действительное число. Но можно пойти и дальше. Не только длина, но и всякий вообще геометрический объект, всякая геометрическая операция могут найти свое место в царстве чисел. Решительный шаг в направлении арифметизации геометрии был сделан не позднее 1629 г. Ферма (1601-1665) и в 1637 г. Декартом (1596-1650). Основная идея аналитической геометрии заключается в использовании "координат" - чисел, связанных (координированных) с данным геометрическим объектом и полностью этот объект характеризующих. Большинству читателей известны так называемые прямоугольные, или декартовы, координаты, служащие для того, чтобы фиксировать положение произвольной точки на плоскости. Мы исходим из двух неподвижных взаимно перпендикулярных прямых на плоскости, "оси х" и "оси у", и к ним относим каждую точку. Эти оси рассматриваются как ориентированные числовые прямые, причем измерение совершается с помощью одного и того же единичного отрезка. Каждой точке Р (рис. 12) сопоставлены две координаты х и у. Они получаются следующим образом. рассмотрим ориентированный отрезок (вектор), идущий из "начала" О в точку Р, и затем спроектируем ортогонально этот вектор на обе оси, получая ориентированный отрезок ОР' на оси х и такой же отрезок OQ' на оси у. Два числа х и y, измеряющие соответственно ориентированную длину отрезков ОР' и OQ' называются координатами точки Р. Обратно, если х и y - два произвольных наперед заданных числа, то соответствующая точка Р определяется однозначно. Если числа х и y оба положительные, то Р попадает в первый квадрант координатной системы (рис. 13); если оба - отрицательные, то в третий; если х положительно, а y отрицательно, то в четвертый и, наконец, если х отрицательно, а y положительно, то во второй.

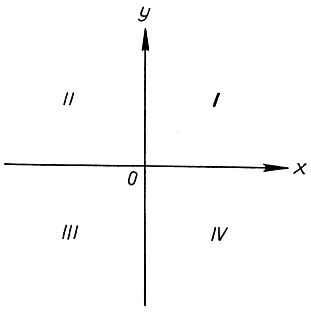
Рис. 13. Четыре квадранта

Расстояние между точкой Р₁ с координатами х₁, у₁ и точкой Р₂ с координатами х₂, у₂ дается формулой

Это немедленно следует из пифагоровой теоремы (рис. 14).

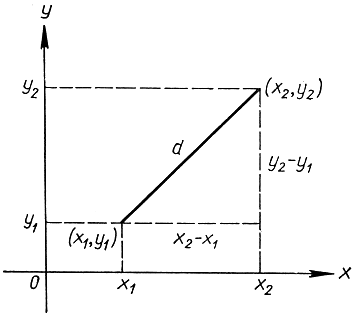
Рис. 14. Расстояние между двумя точками