5. Общее определение иррациональных чисел посредством стягивающихся отрезков

На стр. 89 мы ввели предварительное определение: "число" есть конечная или бесконечная десятичная дробь. Мы условились вместе с тем десятичные дроби, не представляющие рационального числа, называть иррациональными числами. На основе результатов, полученных в предыдущем пункте, мы можем теперь предложить следующую формулировку: "числовой континуум, или система действительных чисел ("действительные" числа противопоставляются здесь "мнимым", или "комплексным", см. § 5), есть совокупность всевозможных бесконечных десятичных дробей". (Приписывая нули, можно, как уже было отмечено, конечную десятичную дробь написать в виде бесконечной, или есть другой способ: последнюю цифру дроби а заменять через а-1 и к ней приписать бесчисленное множество девяток. Так, мы видели, например, что 0,999... = 1. См. п. 3.)

Рациональные числа суть периодические дроби; иррациональные числа суть непериодические дроби. Но и такое определение не представляется вполне удовлетворительным: действительно, мы видели в главе 1, что самой природой вещей десятичная система ничем особым не выделяется из других возможных: таким же образом можно было бы оперировать, на- ' пример, двоичной системой. По этой причине является чрезвычайно желательным дать более общее определение числового континуума, независимое от специального выбора основания ГО или любого иного. Вероятно, простейший метод для введения такого обобщения заключается в следующем.

Рассмотрим на числовой оси некоторую последовательность I₁, I₂, I₃,...,I_n,... отрезков с рациональными концами; предположим, что каждый следующий отрезок содержится в предыдущем и что длина п-го отрезка I_n стремится к нулю при неограниченном возрастании n. Такую последовательность "вложенных" друг в друга отрезков мы будем называть последовательностью стягивающихся отрезков. В случае десятичных отрезков длина I_n равна 10^-n, но с таким же успехом она могла бы равняться, скажем, 2^-n, или можно ограничиться хотя бы тем требованием, чтобы она была меньше 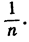Дадим теперь следующую формулировку, которую будем рассматривать как основной геометрический постулат: какова бы ни была последовательность стягивающихся отрезков, существует одна и только одна точка числовой оси, которая одновременно содержится во всех отрезках. (Совершенно ясно, что существует не более одной такой точки, так как длины отрезков стремятся к нулю, а две различные точки не могли бы содержаться в отрезке, длина которого была бы меньше, чем расстояние между точками.) Эта точка по определению и называется действительным числом; если она не является рациональной, то называется иррациональным числом. С помощью такого определения мы устанавливаем полное соответствие между точками и числами. Здесь не прибавлено ничего существенно нового: всего лишь определению числа как бесконечной десятичной дроби придана более общая форма.

Все же читателя в этом месте могут охватить известные сомнения, которые следует признать вполне обоснованными. Что же на самом деле представляет собой та "точка" на числовой оси, которая, как мы допускаем, содержится одновременно во всех стягивающихся отрезках последовательности в случае, если она не соответствует рациональному числу? Наш ответ таков: существование на числовой оси (рассматриваемой как геометрический образ) точки, содержащейся во всех стягивающихся отрезках с рациональными концами, есть основной геометрический постулат. Нет надобности делать редукцию, приводя его к иным математическим предложениям. Мы принимаем его, как принимаем в математике другие аксиомы или постулаты, основываясь на его интуитивной правдоподобности и на его полезности, обнаруживающейся при построении логически последовательной системы математических предложений. Чисто формально мы могли бы исходить из числовой прямой, которую мыслили бы как совокупность одних только рациональных точек, и затем определили бы иррациональную точку как символ, обозначающий некоторую последовательность стягивающихся отрезков. Иррациональная точка полностью определяется последовательностью стягивающихся рациональных отрезков, длины которых стремятся к нулю. Значит, наш основной постулат на самом деле способен служить определением. Принять такое определение, после того как мы были приведены к последовательности стягивающихся отрезков интуитивным ощущением, утверждающим "существование" иррациональной точки,- значит отбросить костыли интуиции, на которые опиралось наше рассуждение, и осознать, что все математические свойства иррациональных точек могут быть понимаемы и представляемы как свойства последовательностей стягивающихся отрезков.

С чисто математической точки зрения в данном случае важно то обстоятельство, что, приняв определение иррационального числа как последовательности стягивающихся отрезков, мы приобретаем возможность дать определения сложения, умножения и т. д.. а также отношений неравенства, являющихся непосредственным обобщением соответствующих определений в поле рациональных чисел, и притом с сохранением всех основных законов, действующих в поле рациональных чисел. Так, например, чтобы определить сумму двух иррациональных чисел α и β, исходя из двух последовательностей стягивающихся отрезков, определяющих числа α и β, построим новую последовательность стягивающихся отрезков, складывая соответственно начальные точки и конечные точки отрезков, входящих в состав данных последовательностей. То же можно сделать с произведением αβ, разностью α-β и частным ^α/_β. И можно показать на основе этих определений, что арифметические законы, рассмотренные в § 1 этой главы при переходе к иррациональным числам, не нарушаются. Подробности, сюда относящиеся, мы опускаем.

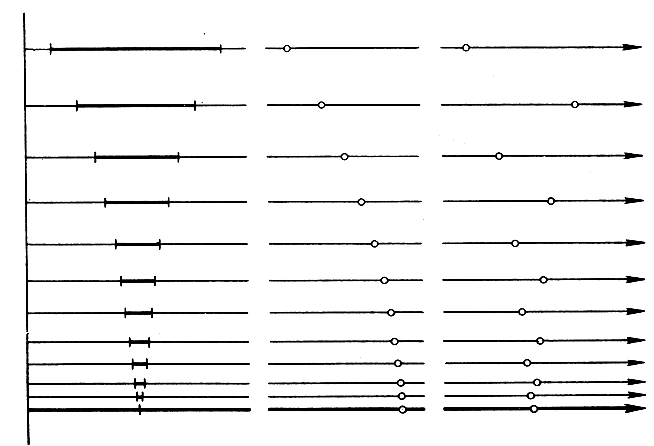
Рис. 11. Стягивающиеся отрезки. Пределы последовательностей

Проверка всех этих законов проста и производится непосредственно без особых затруднений, но могла бы показаться несколько скучноватой начинающему читателю, который, естественно, интересуется скорее тем, что можно сделать с помощью математики, чем анализом ее логических основ. Нередко случается, что новейшие учебники математики отталкивают читателя именно тем, что с первых же страниц дают педантическое обоснование системы действительных чисел. Читатель, спокойно игнорирующий эти страницы, пусть успокоит свою совесть сознанием того факта, что вплоть до конца XIX столетия все великие математики делали свои открытия на основе "наивной" концепции числового континуума, доставляемой непосредственно интуицией.

Наконец, с физической точки зрения, определение иррационального числа посредством последовательности стягивающихся отрезков естественно уподобляется определению числового значения некоторой доступной наблюдению величины - путем ряда измерений, производимых последовательно со все возрастающей точностью. Всякая операция, совершаемая, скажем, с целью определения длины некоторого отрезка, практически осмыслена лишь в пределах некоторой возможной погрешности, величина которой определяет точность инструмента. Так как рациональные числа расположены на прямой всюду плотно, то никакая физическая операция, как бы точна она ни была, не позволит различить, является ли данная длина рациональной или же иррациональной. Таким образом, могло бы показаться, что в иррациональных числах нет никакой необходимости для адекватного описания физических явлений. Но, как мы увидим в главе VI, при математическом описании физических явлений истинное преимущество, приобретаемое посредством привлечения иррациональных чисел, заключается в чрезвычайном упрощении этого описания - именно благодаря свободному использованию понятия предела, основой которого является числовой континуум.