4. Рациональные числа и периодические десятичные дроби

Такие рациональные числа 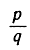, которые не могут быть представлены в виде'конечных десятичных дробей, разлагаются в бесконечные десятичные дроби посредством обыкновенного приема "длинного" деления. На каждой ступени этого процесса возникает остаток, не равный нулю, иначе дробь оказалась бы конечной. Различные возникающие остатки могут быть только целыми числами от 1 до q-1, так что имеется всего q-1 возможностей для значений этих остатков. Это значит, что после q делений некоторый остаток k появится во второй раз. Но тогда все следующие остатки также будут повторяться в том же порядке, в каком они уже появлялись после первого возникновения остатка k. Таким образом, десятичное разложение всякого рационального числа обладает свойством периодичности; после некоторого числа десятичных знаков одна и та же группа десятичных знаков начинает повторяться бесконечное число раз. Например, 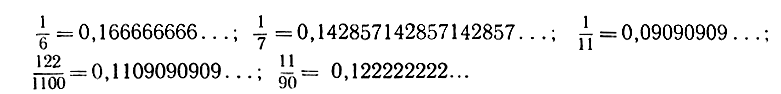и т. д. (Заметим по поводу тех рациональных чисел, которые представляются в виде конечной десятичной дроби, что у этой конечной дроби можно вообразить после последнего ее десятичного знака бесконечно повторяющуюся цифру 0, и, таким образом, рассматриваемые рациональные числа не исключаются из данной выше общей формулировки.) Из приведенных примеров видно, что у некоторых из десятичных разложений, соответствующих рациональным числам, периодическому "хвосту" предшествует непериодическая "голова".

Обратно, можно показать, что все периодические дроби представляют собой рациональные числа. Рассмотрим, например, бесконечную периодическую дробь

Можно написать: 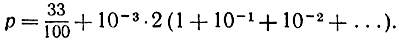Выражение в скобках есть бесконечная геометрическая прогрессия:

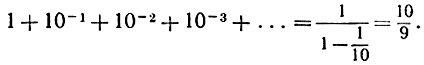
Значит,

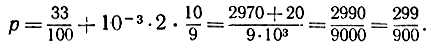
В общем случае доказательство строится таким же образом, но затруднено необходимостью вводить несколько громоздкие обозначения. Рассмотрим периодическую дробь общего вида

Обозначим через В = 0,b₁b₂...b_n периодическую часть нашего разложения.

Тогда можно написать:

Выражение в скобках - бесконечная геометрическая прогрессия, для которой q = 10^-n. Сумма этой прогрессии согласно формуле (10) предыдущего пункта равна 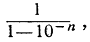и потому

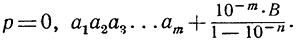
Упражнения. 1) Разложить в десятичные дроби следующие рациональные числа: 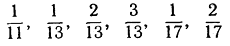и определить периоды разложений.

^*2) Число 142 857 обладает тем свойством, что при умножении его на 2, 3, 4, 5 или 6 в нем совершаются только перестановки цифр. Объяснить это свойство, исходя из разложения числа 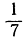в десятичную дробь.

3) Разложить числа, приведенные в упражнении 1, в бесконечные дроби с основаниями 5, 7 и 12.

4) Разложить число 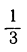в двоичную дробь.

5) Написать разложение 0,11212121 ... . Установить, какое число оно представляет при основаниях 3 или 5.