3. Пределы. Бесконечные геометрические прогрессии

Как мы видели в предыдущем пункте, иногда случается, что некоторое рациональное число s бывает приближаемо последовательностью других рациональных чисел s_n, причем индекс n принимает последовательно все значения 1, 2, 3, ... . Так, например, можно взять: 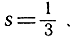причем s₁ = 0,3, s₂ = 0,33, s₃ = 0,333 и т. д. Вот еще пример. Разобьем единичный интервал на две равные части, вторую половину - снова на две равные части, вторую из полученных двух частей - снова на две равные части и т. д., пока наименьший из полученных таким образом интервалов не станет равным 2^-n, где n - сколь угодно большое наперед заданное число, например, n = 100, n = 100 000 и т. д. Затем, складывая вместе все интервалы, кроме самого последнего, мы получаем общую длину

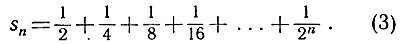
Легко понять, что s_n отличается от 1 на 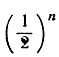и что эта разность становится сколь угодно малой, или "стремится к нулю", при неограниченном возрастании n. Говорить, что эта разность равна нулю, когда n равно "бесконечности", не имеет никакого смысла. Бесконечное в математике связывается с некоторым процессом, не имеющим конца, и никогда не связывается с актуальной величиной. Желая описать поведение s_n, мы говорим, что сумма s_n стремится к пределу 1, когда n стремится к бесконечности, и пишем

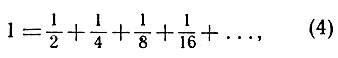
причем то, что возникает справа, есть бесконечный ряд. Последнее "равенство" не следует понимать в том смысле, что имеется в виду сложить бесконечное число слагаемых: это только сокращенная запись того факта, что 1 есть предел конечных сумм s_n, получающийся, когда n стремится к бесконечности (но ни в коем случае не равно бесконечности). Итак, равенство (4), заканчивающееся неопределенным символом "+...", как бы стенографирует некоторую точную мысль, выражаемую по неизбежности длинным рядом слов:

"1 равна пределу (при n, стремящемся к бесконечности) выражения

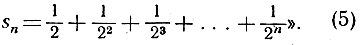
Еще более кратко и выразительно пишут следующим образом:

Говоря о пределах, рассмотрим еще пример. Пусть перед нами имеется бесконечная последовательность различных степеней числа q:

Если -1<q#60;1 например 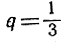или 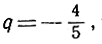то gⁿ стремится к нулю при неограниченном возрастании n. При этом если q - отрицательное число, то знаки qⁿ чередуются: за + следует -, и обратно; таким образом, qⁿ стремится к нулю "с двух сторон". Так, если

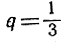, то 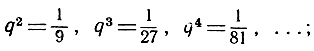если же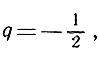

то 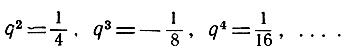Мы утверждаем, что предел qⁿ, когда n стремится к бесконечности, равен нулю, или символически

(Между прочим, если q>1 или q<-1, то qⁿ уже не стремится к нулю, а неограниченно возрастает по абсолютной величине.)

Приведем строгое доказательство утверждения (7). Мы видели на стр. 39-40, что при любом целом положительном значении n и при условии р>-1 имеет место неравенство (1 + p)ⁿ≥ 1 + nр. Пусть q - какое-то положительное число, меньшее единицы, например 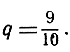Тогда можно положить 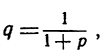где р>0. Отсюда следует:

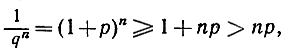
или же (см. определение (4) на стр. 80)

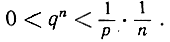
Значит, qⁿ заключено между постоянным числом 0 и числом 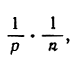которое стремится к нулю при неограниченном возрастании n (так как р - постоянное). После этого ясно, что qⁿ→0. Если q - отрицательное число, то мы положим 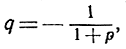и тогда qⁿ будет заключено между числам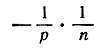и и 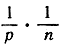рассуждение заканчивается так же, как раньше.

Рассмотрим теперь геометрическую прогрессию

(Случай 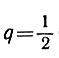был рассмотрен выше.) Как уже было показано (см. стр. 37), сумма s_n может быть представлена в более простой и сжатой форме. Умножая s_n на q, мы получаем:

и, вычитая (8а) из (8), убеждаемся, что все члены, кроме 1 и qⁿ⁺¹, взаимно уничтожаются. В результате будем иметь:

или же, деля на 1-q,

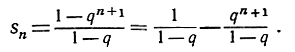
С понятием предела мы встретимся, если заставим п неограниченно возрастать. Мы видели только что, что qⁿ⁺¹ = q*qⁿ стремится к нулю, если -1<q<1, и отсюда можем заключить:

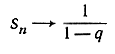при n→∞, если -1<q<1. (9)

Тот же результат можно записать, пользуясь бесконечным рядом

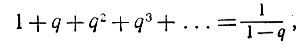если -1<q<1. (10)

Например,

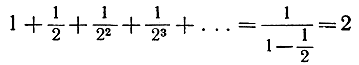
в полном соответствии с равенством (4); подобным же образом

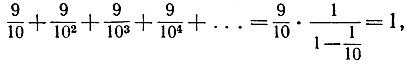
или, иначе, 0,9999 ... = 1. Совершенно так же конечная дробь 0,2374 и бесконечная дробь 0,23739999 ... представляют одно и то же число.

В главе VI мы вернемся к общему обсуждению понятия предела, рассматривая вопрос с современной, логически более строгой точки зрения.

Упражнения. 1) Доказать, что

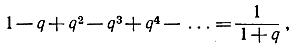если |q|<1.

2) Каков предел последовательности а₁, а₂, а₃, ..., где 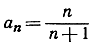(Указание. Напишите данное выражение 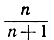в виде 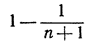обратите внимание на то, что вычитаемое стремится к нулю.)

3) Каков предел 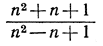при n→∞? (Указание. Напишите это выражение в виде

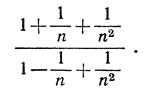
4) Предполагая q по абсолютной величине меньшим чем 1, докажите, что 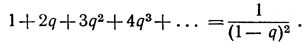(Указание. Воспользуйтесь результатом упражнения 3 на стр. 42.)

5) Каков предел бесконечного ряда

6) Вычислить пределы выражений ,

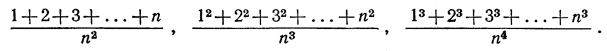
(Указание. Воспользуйтесь результатами, полученными на стр. 36-39.)