2. Десятичные дроби: конечные и бесконечные

Чтобы покрыть числовую ось везде плотным множеством точек, нет необходимости использовать всю совокупность рациональных чисел: достаточно, например, ограничиться только теми числами, которые возникают при подразделении единичного отрезка на 10, потом на 100, 1000 и т. д. равных частей. Получающиеся при этом точки деления соответствуют "десятичным дробям". Так, числу 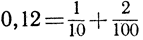соответствует точка, расположенная в первом единичном интервале, во втором "подинтервале" длины 10^-1, и именно она есть начальная точка третьего "подподинтервала" длины 10^-2

(а^-n означает 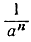). Если такого рода десятичная дробь содержит п знаков после запятой, то она имеет вид:

где z - целое число, а коэффициенты а - цифры 0, 1, 2,..., 9, обозначающие число десятых, сотых и т. д. Сокращенно число f записывается в десятичной системе следующим образом: z, а₁, а₂, a₃ ... a_n. Мы убеждаемся непосредственно, что такого рода десятичные дроби могут быть представлены и в виде обыкновенных дробей 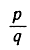, где q = 10ⁿ; так, например, 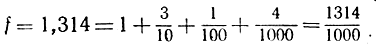Если окажется, что p и q имеют общий множитель, то дробь можно сократить, и тогда знаменатель будет некоторым делителем числа 10ⁿ. С другой стороны, несократимая дробь, у которой знаменатель не есть делитель некоторой степени 10, не может быть представлена в виде десятичной дроби указанного типа. Например, 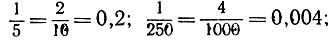но 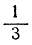не может быть написана как десятичная дробь с конечным числом n десятичных знаков, как бы ни было велико n: в самом деле, из равенства вида

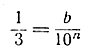
следовало бы

а последнее равенство невозможно, так как 3 не входит множителем ни в какую степень числа 10.

Возьмем теперь на числовой оси какую-нибудь точку Р, которая не соответствует никакой конечной десятичной дроби; можно, например,

взять рациональную точку 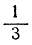или иррациональную точку √2. Тогда в процессе последовательного подразделения единичного интервала на 10 равных частей точка Р никогда не окажется в числе точек деления: она будет находиться внутри десятичных интервалов, длина которых будет неограниченно уменьшаться; концы этих интервалов соответствуют конечным десятичным дробям и приближают точку Р с какой угодно степенью точности. Рассмотрим несколько подробнее этот процесс приближения.

Предположим, что точка Р лежит в первом единичном интервале. Сделаем подразделение этого интервала на 10 равных частей, каждая длины 10^-1, и предположим, что точка Р попадает, скажем, в третий из этих интервалов. На этой стадии мы можем утверждать, что Р заключена между десятичными дробями 0,2 и 0,3. Подразделяем снова интервал от 0,2 до 0,3 на 10 равных частей, каждая длины 10^-2, и обнаружим, что Р попадает, допустим, в четвертый из этих интервалов. Подразделяя его, как раньше, видим, что точка Р попадает в первый интервал длины 10^-3. Теперь можно сказать, что точка Р заключена между 0,230 и 0,231. Этот процесс может быть продолжен до бесконечности и приводит к бесконечной последовательности цифр а₁, а₂, а₃, ... , а_n, ... , обладающей таким свойством: каково бы ни было n, точка Р заключена в интервале I_n, у которого начальная точка есть 0, а₁а₂а₃ ...а_n-1а_n, а конечная - 0, а₁а₂а₃ ... а_n-1 (а_n + 1), причем длина I_n равна 10^-n. Если станем полагать по порядку n = 1,2, 3, 4,..., то увидим, что каждый из интервалов I₁, I₂, I₃, ... содержится в предыдущем, причем их длины 10^-1, 10^-2, 10^-3,... неограниченно уменьшаются. Мы скажем, более кратко, что точка Р заключена в стягивающуюся последовательность десятичных интервалов. Например, если точка Р есть 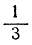, то все цифры а₁, а₂, а₃,... равны 3, и Р заключена в любом интервале I_n от 0,333 ... 33 до 0,333 ... 34, т. е. 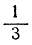больше, чем 0,333... 33, и меньше, чем 0,333...34, сколько бы ни взять цифр после запятой. Мы скажем в этих обстоятельствах, что n-значная десятичная дробь 0,333 ... 33 "стремится к 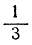, когда число цифр n неограниченно возрастает. И мы условимся писать

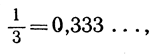
причем точки означают, что десятичная дробь может быть продлена "до бесконечности".

Иррациональная точка √2, которая была рассмотрена в пункте 1, также приводит к бесконечной десятичной дроби. Но закон, которому подчиняются последовательные цифры десятичного разложения, на этот раз далеко не очевиден. Мы затрудняемся указать формулу, которая давала бы цифру, стоящую на n-м месте, хотя можно вычислить столько цифр, сколько мы пожелали бы себе заранее назначить:

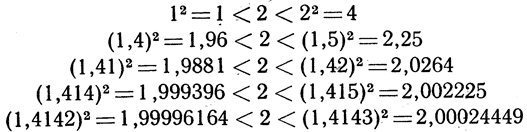
и т. д.

В качестве общего определения мы скажем, что точка Р, которая не может быть представлена в виде десятичной дроби с конечным числом десятичных знаков, представляется в виде бесконечной десятичной дроби z, а₁а₂а₃..., если, каково бы ни было n, точка Р лежит в интервале длины 10"" с начальной точкой z, a₁а₂а₃ ... а_n.

Таким образом, мы устанавливаем соответствие между всеми точками числовой оси и всеми (конечными и бесконечными) десятичными дробями. Теперь мы попытаемся ввести предварительное определение: "число" есть конечная или бесконечная десятичная дробь. Те бесконечные десятичные дроби, которые не представляют рационального числа, называются иррациональными числами. До середины XIX столетия соображения, подобные приведенным выше, казались достаточными для объяснения того, как устроена система рациональных и иррациональных чисел - числовой континуум. Необычайные успехи математики, достигнутые начиная с XVII столетия, в частности развитие аналитической геометрии и дифференциального и интегрального исчислений, твердо базировались именно на таком представлении о системе чисел. Однако'в период критического пересмотра принципов и консолидации результатов стало ощущаться все более и более явственно, что понятие иррационального числа должно быть подвергнуто более точному и глубокому анализу. Но, прежде чем перейти к очерку современной теории числового континуума, нам придется рассмотреть и разобрать - на более или менее интуитивной основе - одно из математических понятий капитальной значимости - понятие предела.

Упражнение. Вычислить приближенно 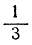и 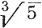с ошибкой, не превышающей 10^-2.