§ 2. Несоизмеримые отрезки. Иррациональные числа, пределы

1. Введение

Если мы станем сравнивать по величине два прямолинейных отрезка а и b, то не исключена возможность, что а содержится в b в точности целое число раз r. В таком случае длина отрезка b очень просто выражается через длину отрезка а: длина b в r раз больше, чем длина а. Может случиться и так, что целого числа r, которое обладало бы указанным свойством, не существует; но при этом возможно, что, разделив отрезок а на некоторое число, скажем я, равных частей (каждая длины 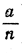) и взяв целое число m таких частей, мы в точности получим отрезок b:

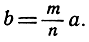
(1)

Если осуществляется соотношение вида (1), то говорят, что два отрезка а и b соизмеримы, так как они обладают некоторой "общей мерой": таковой является отрезок длины 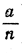, который содержится в отрезке а ровно n раз, а в отрезке b ровно m раз. Некоторый отрезок b соизмерим или несоизмерим с отрезком а в зависимости от того, можно или нельзя подобрать два таких натуральных числа m и n (n≠0), что имеет место равенство (1). Обращаясь к рис. 9, предположим, что в качестве отрезка а избран единичный отрезок [0,1], и рассмотрим всевозможные отрезки, у которых один из концов совпадает с 0. Тогда из этих отрезков будут соизмеримы с единичным отрезком те и только те, у которых второй конец совпадает с некоторой рациональной точкой .

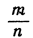Для практической цели измерения рациональных чисел всегда совершенно достаточно. Даже с точки зрения теоретической, поскольку рациональные точки расположены всюду плотно, могло бы показаться, что все точки на числовой оси рациональные. Если бы дело обстояло именно так, то всякий отрезок был бы соизмерим с единичным. Но дело обстоит не так просто, и в установлении этого обстоятельства заключается одно из самых поразительных открытий в математике: оно было сделано уже в древнейшие времена (в школе Пифагора). Существуют несоизмеримые отрезки, или, иначе (если мы допустим, что каждому отрезку соответствует некоторое число, выражающее его длину), существуют иррациональные числа. Осознание этого факта было научным событием величайшей значимости, почти откровением. Весьма возможно, что именно оно положило начало тому, что мы теперь считаем строгим математическим методом и рассматриваем как вклад в науку, сделанный древними греческими математиками. Без сомнения, это замечательное открытие глубоко повлияло на всю математику и даже философию от древних времен и до наших дней.

Евдоксова теория несоизмеримых величин, изложенная в геометрической форме в "Началах" Евклида, представляет собой тончайшее достижение греческой математики (ее изложение обыкновенно пропускается в разжиженных пересказах Евклида, предназначенных для школьного обучения). Эта теория получила подобающую ей высокую оценку лишь в конце XIX столетия - после того, как усилиями Дедекинда, Кантора и Вейерштрасса была создана строгая теория иррациональных чисел. Мы изложим в дальнейшем эту теорию в ее современном арифметическом аспекте.

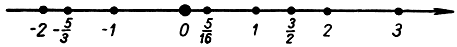
Рис. 9. Рациональные точки

Прежде всего установим: диагональ квадрата несоизмерима с его стороной. Предположим, что сторона квадрата избрана в качестве единицы длины, длину же диагонали обозначим через х. Тогда согласно теореме Пифагора мы получаем:

(Такое число х обозначают символом √2) Если бы х было соизмеримо с единицей, то можно было бы найти два таких целых числа р и q, что 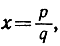и тогда мы пришли бы к равенству

Можно допустить, что дробь 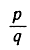несократима, иначе мы с самого начала сократили бы ее на общий наибольший делитель чисел р и q. С правой стороны имеется 2 в качестве множителя, и потому р² есть четное число, и, значит, само р - также четное, так как квадрат нечетного числа есть нечетное число. В таком случае можно положить р = 2r. Тогда равенство (2) принимает вид:

Так как с левой стороны теперь имеется 2 в качестве множителя, значит, q², а следовательно, и q - четное. Итак, и р и q - четные числа, т. е. делятся на 2, а это противоречит допущению, что дробь 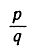несократима. Итак, равенство (2) невозможно, и x не может быть рациональным числом.

Иначе этот результат можно сформулировать, утверждая, что √2 есть число иррациональное.

Только что приведенное рассуждение показывает, что иной раз самое простейшее геометрическое построение приводит к отрезку, несоизмеримому с единицей. Если такой отрезок будет отложен с помощью циркуля на числовой оси от точки 0, то построенная таким образом точка (конец отрезка) не совпадает ни с какой рациональной точкой. Итак, система рациональных точек (хотя и всюду плотная) не покрывает всей числовой оси. Наивному сознанию, несомненно, может показаться странным и парадоксальным, что всюду плотное множество рациональных точек не покрывает всей прямой, Никакая наша "интуиция" не поможет нам "увидеть" иррациональные точки или отличить их от рациональных. Нет ничего удивительного в том, что открытие несоизмеримого потрясло греческих математиков и мыслителей и что его существование и в наши дни продолжает производить впечатление на людей, склонных к углубленным размышлениям.

Не представило бы труда конструировать столько отрезков, несоизмеримых с единицей, сколько бы мы пожелали. Концы всех таких отрезков - при условии, что их начала совпадают с точкой 0,- образуют совокупность иррациональных точек. Заметим теперь, что нашим руководящим принципом уже при введении рациональных дробей было желание обеспечить возможность измерения длин отрезков посредством чисел, и тот же принцип продолжает руководить нами и тогда, когда речь идет о несоизмеримых отрезках. Если мы требуем, чтобы существовало взаимное соответствие между числами, с одной стороны, и точками на прямой линии -с другой, то неизбежно приходится ввести в рассмотрение иррациональные числа.

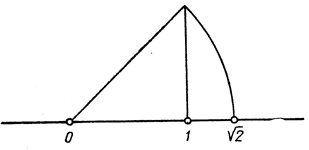
Рис. 10. Построение числа √2

Подводя итоги до сих пор сказанному, мы констатируем, что иррациональное число обозначает длину отрезка, несоизмеримого с единицей. В следующих разделах мы должны будем уточнить это несколько смутное и всецело геометрическое определение и в результате придем к определению, более удовлетворительному с точки зрения логической строгости. Рассматривая этот вопрос, мы будем вначале исходить из десятичных дробей.

Упражнения. 1) Докажите, что числа 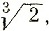√3, √5, 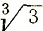иррациональные. (Указание. Воспользуйтесь леммой на стр. 71.)

2) Докажите, что числа √2 + √3 и √2 + 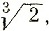иррациональные. (Указание. Если бы, например, первое из этих чисел было рациональным числом r, то, написав √3 = r - √2 и возведя в квадрат, мы заключили бы, что √2 есть рациональное число.)

3) Докажите, что число √2 + √3 + √5 иррациональное. Попробуйте придумать подобные и более общие примеры.