3. Геометрическое представление рациональных чисел

Выразительное геометрическое представление системы рациональных чисел может быть получено следующим образом.

Рис. 8. Числовая ось

На некоторой прямой линии, "числовой оси", отметим отрезок от О до 1 (рис. 8). Тем самым устанавливается длина единичного отрезка, которая, вообще говоря, может быть выбрана произвольно. Положительные и отрицательные целые числа тогда изображаются совокупностью равноотстоящих точек на числовой оси, именно положительные числа отмечаются вправо, а отрицательные - влево от точки 0. Чтобы изобразить числа со знаменателем n, разделим каждый из полученных отрезков единичной длины на n равных частей; точки деления будут изображать дроби со знаменателем n. Если сделаем так для значений n, соответствующих всем натуральным числам, то каждое рациональное число будет изображено некоторой точкой числовой оси. Эти точки мы условимся называть "рациональными"; вообще, термины "рациональное число" и "рациональная точка" будем употреблять как синонимы.

В главе I, § 1 было определено соотношение неравенства А<В для натуральных чисел. На числовой оси это соотношение отражено следующим образом: если натуральное число А меньше, чем натуральное число В, то точка А лежит левее точки В. Так как указанное геометрическое соотношение устанавливается для любой пары рациональных точек, то естественно пытаться обобщить арифметическое отношение неравенства таким образом, чтобы сохранить этот геометрический порядок для рассматриваемых точек. Это удается, если принять следующее определение: говорят, что рациональное число А меньше, чем рациональное число В (А<В), или что число В больше, чем число А (В>А), если разность В-А положительна. Отсюда следует (при A<B), что точки (числа) между А и В - это те, которые одновременно >A и <В. Каждая такая пара точек А и В, вместе со всеми точками между ними, называется сегментом (или отрезком) и обозначается [А, В] (а множество одних только промежуточных точек - интервалом (или промежутком), обозначаемым (А, В)).

Расстояние произвольной точки А от начала 0, рассматриваемое как положительное число, называется абсолютной величиной А и обозначается символом

Понятие "абсолютная величина" определяется следующим образом: если A≥0, то |А| = А; если A<0, то |A| = - А. Ясно, что если числа А и В имеют один и тот же знак, то справедливо равенство |А + В| = |А| + |В|; если же А и В имеют разные знаки, то |А + В|<|А| + |В|. Соединяя эти два результата вместе, мы приходим к общему неравенству

которое справедливо независимо от знаков А и В.

Факт фундаментальной важности выражается следующим предложением: рациональные точки расположены на числовой прямой всюду плотно. Смысл этого утверждения тот, что внутри всякого интервала, как бы он ни был мал, содержатся рациональные точки. Чтобы убедиться в справедливости высказанного утверждения, достаточно взять число n настолько большое, что интервал 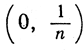будет меньше, чем данный интервал (A, В); тогда по меньшей мере одна из точек вида 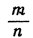окажется внутри данного интервала. Итак, не существует такого интервала на числовой оси (даже самого маленького, какой только можно вообразить), внутри которого не было бы рациональных точек. Отсюда вытекает дальнейшее следствие: во всяком интервале содержится бесконечное множество рациональных точек. Действительно, если бы в некотором интервале содержалось лишь конечное число рациональных точек, то внутри интервала, образованного двумя соседними такими точками, рациональных точек уже не было бы, а это противоречит тому, что только что было доказано.