2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения

Независимо от "практического" основания для введения рациональных чисел существует основание более глубокое и носящее в известном смысле еще более принудительный характер. Эту сторону дела мы рассмотрим здесь совершенно независимо от приведенных выше рассуждений. В обычной арифметике натуральных чисел мы всегда можем выполнять основные прямые операции - сложение и умножение. Но обратные операции - вычитание и деление - не всегда выполнимы. Разность b-а двух натуральных чисел а и b есть по определению такое натуральное число с, что а + с = b, т. е. это есть решение уравнения а + х = b. Но в области натуральных чисел символ b - а имеет смысл лишь при ограничении b>а, так как только при этом условии уравнение а + х = b имеет решением натуральное число. На пути к снятию этого ограничения серьезный шаг был сделан уже тогда, когда был введен символ 0 для обозначения а - а. Но еще более значительным успехом было введение символов -1,-2,-3, ... и вместе с тем определения

для случая b<a: после этого можно было утверждать, что и вычитание обладает свойством неограниченной выполнимости в области всех целых - положительных и отрицательных - чисел. Вводя новые символы -1,-2, -3,... и тем самым расширяя числовую область, мы обязаны, конечно, определить операции со вновь вводимыми числами таким образом, чтобы первоначальные правила арифметических операций не были нарушены.

Так, например, правило

которое лежит в основе умножения отрицательных чисел, есть следствие нашего желания сохранить дистрибутивный закон а(b + с) = ab + ас. Действительно, если бы мы, скажем, декларировали, что (-1)*(-1) = -1, то, полагая а = -1, b = 1, с = -1, получили бы -1(1-1) = -1 - 1 = -2, тогда как на самом деле -1(1 - 1) = -1*0 = 0.

Понадобилось немало "времени, чтобы среди математиков было хорошо осознано, что "правило знаков" (3) и вместе с ним все прочие определения, относящиеся как к отрицательным числам, так и к дробям, никак не могут быть "доказаны". Они создаются, или декларируются, нами самими с с целью обеспечить свободу операций и притом без нарушения основных арифметических законов. Что может - и должно - быть доказываемо, так это только то, что если эти определения приняты, то тем самым сохранены основные законы арифметики: коммутативный, ассоциативный и дистрибутивный. Даже великий Эйлер пользовался совершенно неубедительной аргументацией, желая показать, что (-1)*(-1) "должно" равняться + 1. Он говорил: "Рассматриваемое произведение может быть только или +1, или -1; но (-1) быть не может, так как -1 =(+1)*(-1)".

Совершенно подобно тому, как введение отрицательных целых чисел и нуля расчищает путь для неограниченной выполнимости вычитания, введение дробных чисел устраняет арифметические препятствия, мешающие выполнять деление. Отношение, или частное, х = ^b/_a двух целых чисел определяется как решение уравнения

и существует как целое число только в том случае, если а есть делитель b. Но если это не так (например, при а = 2, b = 3), то мы просто вводим новым символ 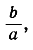называемый дробью и подчиненный условию, выражающемуся равенством 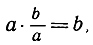, так что ^b/_a есть решение (4) "по определению".

Изобретение дробей как новых числовых символов обеспечивает неограниченную выполнимость деления, кроме деления на нуль, которое исключается раз навсегда.

Выражения вроде 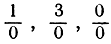и т. п. останутся для нас символами, лишенными смысла. Если бы мы допустили деление на 0, то из верного равенства 0*1 =0*2 вывели бы неверное следствие 1 = 2. Как-никак, иногда бывает целесообразно обозначать такие выражения символом "бесконечность", однако с условием, чтобы не делалось даже попытки оперировать этим символом так, как будто бы он подчинялся обычным законам арифметики.

Теперь нам ясны принципы, согласно которым сконструирована система всех рациональных чисел - целых и дробных, положительных и отрицательных. В этой расширенной области не только полностью оправдываются формальные законы - ассоциативный, коммутативный и дистрибутивный,- но и уравнения а + х = b и ах = b всегда имеют решения х = b - а и 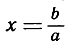единственной оговоркой, что во втором случае а не должно равняться нулю. Иными словами, в области рациональных чисел так называемые рациональные операции - сложение, вычитание, умножение и деление - выполнимы неограниченно и не выводят за пределы области. Такие замкнутые числовые области называются полями. Мы встретимся с дальнейшими примерами полей ниже, в этой же главе, а также в главе III.

Расширение области посредством введения новых символов, совершаемое таким образом, что законы, которые имели место в первоначальной области, сохраняются и в расширенной, является типичным примером характерного для математики принципа обобщения. Переход путем обобщения от натуральных чисел к рациональным удовлетворяет одновременно и теоретической потребности в снятии ограничений, которые наложены на вычитание и деление, и вместе с тем - практической потребности в числах, пригодных для фиксации результатов измерений. Именно тот факт, что рациональные числа идут навстречу сразу теоретической и практической потребностям, придает им особую важность. Как мы видели, расширение понятия числа совершилось путем введения новых абстрактных символов вроде 0-2 или 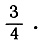В наше время мы оперируем этими символами бегло и уверенно, не вдумываясь в их природу, и трудно даже себе представить, что еще в XVII столетии они пользовались доверием гораздо в меньшей степени, чем натуральные числа, что ими, если и пользовались, то с известным сомнением и трепетом. Свойственное человеческому сознанию стремление цепляться за "конкретное" - воплощаемое в ряде натуральных чисел - обусловливает ту медленность, с которой протекала неизбежная эволюция. Логически безупречная арифметическая система может быть сконструирована не иначе, как в отвлечении от действительности.