§ 1. Рациональные числа

1. Рациональные числа как средство измерения

Натуральные числа возникают как абстракция в процессе счета объектов, образующих конечные совокупности. Но в повседневной жизни нам приходится не только считать объекты, индивидуально отделенные один от другого, но и измерять величины, например, такие, как длина, площадь, вес, время. Если мы хотим обеспечить свободу операций с результатами измерения таких величин, могущих неограниченно делиться на части, нам необходимо, не ограничиваясь натуральным рядом, расширить пределы арифметики и создать новый мир чисел. Первый шаг заключается в том, чтобы проблему измерения свести к проблеме счета. Мы выбираем сначала совершенно произвольно единицу измерения - фут, ярд, дюйм, фунт, грамм - смотря по случаю, и этой единице приписываем меру 1. Затем мы считаем число таких единиц, входящих в измеряемую величину. Может случиться, что данный кусок свинца весит ровно 54 фунта. Но в общем случае, как мы замечаем, процесс счета "не сходится": данная величина не измеряется абсолютно точно выбранной единицей, не оказывается ей кратной. Самое большее, что мы можем сказать в этом случае,- это то, что она заключена между двумя последовательными кратными этой единицы, допустим, между 53 и 54 фунтами. Если так действительно происходит, то мы делаем следующий шаг и вводим новые подъединицы, получающиеся от подразделения первоначальной единицы на некоторое число n равных частей. На разговорном языке эти новые подъединицы могут иметь те или иные названия; например, фут подразделяется на 12 дюймов, метр - на 100 сантиметров, фунт - на 16 унций, час - на 60 минут, минута - на 60 секунд и т. п. Однако в общей математической символике подъединица, получаемая при подразделении первоначальной единицы на n частей, обозначается символом ¹/_n и если рассматриваемая величина содержит ровно m таких подъединиц, то ее мера тогда есть ^m/_n. Этот символ называется дробью, или отношением (иногда пишут m:n). Последний, и самый существенный, шаг был совершен уже осознанно, после многих столетий накопления отдельных усилий: символ ^m/_n был освобожден от его конкретной связи с процессом измерения и самими измеряемыми величинами и стал рассматриваться как отвлеченное число, самостоятельная сущность, уравненная в своих правах с натуральным числом. Если m и n - натуральные числа, то символ ^m/_n называется рациональным числом.

Употребление термина "число" (первоначально под "числами" понимали только натуральные числа) применительно к новым символам оправдывается тем обстоятельством, что сложение и умножение этих символов подчиняется тем же законам, что и соответствующие операции над натуральными числами. Чтобы в этом убедиться, нужно сначала определить, в чем заключается сложение и умножение рациональных чисел, а также определить, какие рациональные числа признаются равными между собой. Эти определения, как всем известно, таковы:

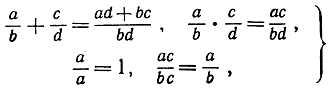
где а, b, с, d - произвольные натуральные числа. Например:

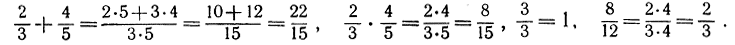
Эти самые определения мы вынуждены принять, если имеем в виду использовать рациональные числа для измерения длин, площадей и т. п. Но с более строгой логической точки зрения эти правила сложения и умножения и это толкование равенства по отношению ко вновь вводимым символам устанавливаются независимо по определению, не будучи обусловлены какой-либо иной необходимостью, кроме взаимной совместимости (непротиворечивости) и пригодности к практическим приложениям. Исходя из определений (1), можно показать, что основные законы арифметики натуральных чисел продолжают сохраняться и в области всех рациональных чисел:

Так, например, доказательство коммутативного закона сложения в случае дробей ясно из следующих равенств:

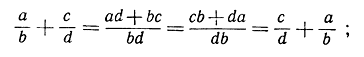
здесь первое и последнее равенства оправдываются определением сложения (1), а среднее есть следствие коммутативных законов сложения и умножения в области натуральных чисел. Читатель сможет, если пожелает, проверить таким же образом четыре остальных закона.