6. Иные методы определения иррациональных чисел. Дедекиндовы сечения

Несколько иной путь для определения иррациональных чисел был избран Рихардом Дедекиндом (1831-1916), одним из самых выдающихся основоположников логического и философского анализа основ математики. Его статьи - "Stetigkeit und irrationale Zahlen"^* (1872) и "Was sind und was sollen die Zahlen?"^** (1887) - оказали глубокое влияние на исследование основных принципов математики. Дедекинд предпочитал общие абстрактные концепции конкретным построениям вроде последовательностей стягивающихся отрезков. Его процедура базируется на идее "сечения"; мы сейчас опишем, что это такое.

^* ("Непрерывность и иррациональные числа".)

^** ("Что такое числа и чем они должны быть?)

Предположим, что каким-то способом удалось разбить совокупность всех рациональных чисел на два класса А и В таким образом, что всякое число b класса В больше, чем всякое число а класса А. Всякое разбиение такого рода называется сечением в области рациональных чисел.- Если произведено сечение, то должна осуществиться одна из следующих трех логически мыслимых возможностей.

1. Существует наибольший элемент а^* в классе А. Такое положение вещей имеет место, например, в том случае, если к классу А отнесены все рациональные числа ≤1, к классу В - все рациональные числа >1.
2. Существует наименьший элемент b^* в классе В. Это происходит, например, в том случае, если к классу А отнесены все рациональные числа <1, к классу В - все рациональные числа ≥1.
3. Нет ни наибольшего элемента в классе А, ни наименьшего в классе В. Сечение этого рода получится, например, в том случае, если к классу А отнесены все рациональные числа, квадрат которых меньше чем 2, а к классу В - все рациональные числа, квадрат которых больше чем 2. Классами А и В исчерпываются все рациональные числа, так как было показано, что такого рационального числа, квадрат которого равен 2, не существует.

Такой случай, когда в классе А есть наибольший элемент а^* и вместе с тем в классе В - наименьший элемент b^*, логически невозможен, так как тогда рациональное число 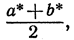заключенное как раз между а^* и b^*, было бы больше, чем наибольший элемент в A, и меньше, чем наименьший элемент в В, и, значит, не могло бы принадлежать ни к A, ни к В.

В третьем случае, когда нет ни наибольшего рационального числа в классе A, ни наименьшего - в классе В, тогда, по Дедекинду, сечение определяет, или, лучше, представляет собой, некоторое иррациональное число. Не представляет труда проверить, что определение Дедекинда согласуется с определением, в основе которого находятся вложенные отрезки: из всякой последовательности вложенных отрезков I₁, I₂, I₃,... мы получаем сечение, если отнесем к классу A все те рациональные числа, которые меньше, чем левый конец хотя бы одного I_n, к классу В - все прочие рациональные числа.

В философском отношении определение иррациональных чисел по Дедекинду находится на более высоком уровне абстракции, так как оно не ограничивает ни в чем того математического закона, который определяет классы A и В. Другой, более конкретный метод для определения континуума действительных чисел принадлежит Георгу Кантору (1845-1918). На первый взгляд резко отличный как от метода вложенных отрезков, так и от метода сечений, он, однако, эквивалентен любому из них в том смысле, что числовой континуум, получающийся на основе всех трех методов, обладает одними и теми же свойствами. Идея Кантора исходит из того, что 1) действительные числа можно трактовать как бесконечные десятичные дроби, 2) бесконечные десятичные дроби можно рассматривать как пределы конечных десятичных дробей. Чтобы не связывать себя зависимостью от десятичных дробей, мы, следуя Кантору, принимаем, что всякая "сходящаяся" последовательность рациональных чисел а₁, а₂, а₃, ... определяет действительное число. При этом "сходимость" понимается в том смысле, что разность (а_m-а_n) между двумя членами последовательности стремится к нулю, если тип одновременно и независимо друг от друга неограниченно возрастают. (Как раз последовательные десятичные приближения обладают этим свойством: любые два из них после n-го отличаются меньше чем на 10^-n.) Так как одно и то же действительное число по методу Дедекинда может быть определяемо самыми разнообразными последовательностями рациональных чисел, то приходится добавить, что две последовательности а₁, а₂, а₃, ... и b₁, b₂, b₃, ... определяют одно и то же действительное число, если разность а_m-b_n стремится к нулю при неограниченном возрастании n. Определить, идя по пути, намеченному Дедекиндом, сложение и т. д. не представляет труда.