§ 3. Пифагоровы числа и большая теорема Ферма

Интересный вопрос из области теории чисел связан с теоремой Пифагора. Теорема эта, как известно, алгебраически выражается равенством

где а и b - длины катетов, а с - длина гипотенузы. Проблема разыскания всех прямоугольных треугольников, стороны которых выражаются целыми числами, таким образом, эквивалентна проблеме нахождения всех решений (а, b, с) в целых числах уравнения (1). Каждая тройка целых чисел (а, b, с), удовлетворяющих этому уравнению, носит название пифагоровой тройки.

Все пифагоровы тройки могут быть найдены довольно просто. Пусть целые числа а, b и с образуют пифагорову тройку, т. е. связаны соотношением а² + b² = с². Положим ради краткости 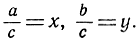Тогда х и у - рациональные числа, связанные равенством х² + у² = 1. Из последнего следует: у² = (1 - х) (1 + х) или 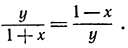Общее значение двух отношений в полученной пропорции есть число t, которое может быть представлено как отношение двух целых чисел 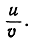Можно, далее, написать: у = t (1 + x) и (1 - х) = ty, или же

Из полученной системы уравнений немедленно следует, что

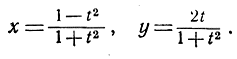
Подставляя 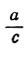и 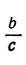вместо х и у и 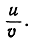вместо t, будем иметь:

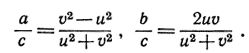
Отсюда вытекает:

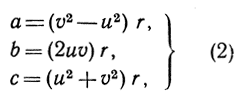
где r - некоторый рациональный множитель пропорциональности. Итак, если числа (а, b, с) образуют пифагорову тройку, то они соответственно пропорциональны числам вида v² - u², 2uv, u² + v². Обратно, легко проверить, что всякие три числа (а, b, с), определенные равенствами вида (2), образуют пифагорову тройку, так как из равенств (2) следует:

так что а² + b² = с².

Этот результат можно несколько упростить. Из некоторой пифагоровой тройки (а, b, с) легко выводится бесконечное множество других пифагоровых троек (sa, sb, sc), каково бы ни было целое положительное s. Так, из (3, 4, 5) получаются (6, 8, 10), (9, 12, 15) и т. д. Такие тройки не являются существенно различными, так как соответствуют подобным треугольникам. Мы условимся говорить о примитивной пифагоровой тройке, если числа а, b и с не имеют общего множителя. Можно показать, что формулы

где u и v - произвольные целые положительные числа (v>v), не имеющие общих множителей и не являющиеся одновременно нечетными, дают нам все примитивные пифагоровы тройки.

^*Упражнение. Докажите последнее утверждение.

Вот примеры примитивных пифагоровых троек:

• v = 2, u = 1 (3, 4, 5);
• v = 3, u = 2 (5, 12, 13);
• v = 4, u = 3 (7, 24, 25);
• v = 10, u = 7 (51, 140, 149) и т. д.

В связи с рассмотрением пифагоровых чисел более или менее естественно возникает вопрос о возможности следующего обобщения задачи: можно ли найти такие целые положительные числа а, b, с, которые удовлетворяли бы уравнению а³ + b³ = с³ или уравнению а⁴ + b⁴ = с⁴, или, вообще, уравнению

где показатель n - целое число,, большее 2? Ответ был дан Ферма, который пришел к нему умозрительным путем. Ферма изучал одно сочинение Диофанта, известного математика древности, занимавшегося теорией чисел, и имел обыкновение делать примечания на полях книги. Хотя он не затруднял себя тем, чтобы приводить тут же доказательства многих высказанных им теорем, все они постепенно в дальнейшем были доказаны - за одним весьма значительным исключением. По поводу пифагоровых чисел Ферма сделал пометку, что уравнение (3) неразрешимо в целых числах, если n>2, но что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было поместить на полях книги, с которой он работал.

Это утверждение Ферма в его общей форме никогда и никем впоследствии не было ни доказано, ни опровергнуто, несмотря на усилия целого ряда крупнейших математиков. Правда, теорема была доказана для очень многих значений n, в частности, для всех n<619, но не для всех возможных значений n; вместе с тем не было указано и примера, опровергающего теорему. Хотя сама по себе теорема и не имеет очень большого значения в математическом смысле, но попытки доказать ее положили начало многим важнейшим исследованиям в области теории чисел. Проблема вызвала большой интерес и в более широких кругах - отчасти благодаря премии размером в 100 000 марок, предназначенной для лица, которое впервые даст решение, причем присуждение премии было поручено Гёттингенской Академии. Пока послевоенная инфляция в Германии не свела на нет денежную ценность этой премии, ежегодно представлялось громадное число "решений", содержащих ошибки. Даже специалисты-математики не раз бывали вводимы в заблуждение и представляли или публиковали доказательства, которые затем отпадали после обнаружения в них иной раз каких-нибудь поверхностных недосмотров. Со времени падения курса марки ажиотаж около проблемы Ферма несколько приутих; и все же время от времени пресса не перестает осведомлять нас о том, что решение найдено каким-нибудь новоявленным "гением".