3. Квадратические вычеты

Обращаясь снова к примерам, иллюстрирующим теорему Ферма, мы можем подметить, что не только всегда справедливо сравнение а^р-1 ≡ 1 (mod р), но (предположим, что р есть простое число, отличное от 2, значит,- нечетное, р = 2р' + 1) при некоторых значениях а справедливо также сравнение 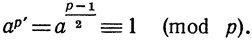Это обстоятельство вызывает ряд заслуживающих внимания соображений. Теорему Ферма можно записать в следующем виде:

Так как произведение делится на р только в том случае, если один из множителей делится на р, то, значит, одно из чисел а^p' - 1 или а^p' + 1 должно делиться на р; поэтому, каково бы ни было простое число р>2 и каково бы ни было число а, не делящееся на р, непременно должно иметь место одно из двух сравнений:

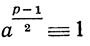
или

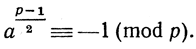
Начиная с самого возникновения современной теории чисел математики были заинтересованы выяснением вопроса: для каких чисел а оправдывается первое сравнение, а для каких - второе? Предположим, что а сравнимо по модулю р с квадратом некоторого числа х,

Тогда 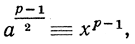и согласно теореме Ферма правая, а следовательно, и левая части сравнения должны быть сравнимы с 1 по модулю р. Такое число а (не являющееся кратным р), которое по модулю р сравнимо с квадратом некоторого числа, называется квадратическим вычетом р; напротив, число Ь, не кратное р, которое не сравнимо ни с каким квадратом по модулю р, называется квадратическим невычетом р. Мы только что видели, что всякий квадратический вычет а числа р удовлетворяет сравнению 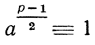Довольно легко установить, что всякий невычет b числа р удовлетворяет сравнению 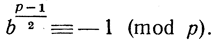Кроме того, мы покажем (несколько дальше), что среди чисел 1, 2, 3, ..., р-1 имеется в точности 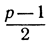квадратических вычетов и 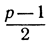невычетов.

Хотя с помощью прямых подсчетов можно было собрать немало эмпирических данных, но открыть сразу общие законы., регулирующие распределение квадратических вычетов, было нелегко. Первое глубоко лежащее свойство этих вычетов было подмечено Лежандром (1752-1833); позднее Гаусс назвал его законом взаимности. Этот закон касается взаимоотношения между двумя различными простыми числами р и q. Он заключается в следующем:

1) Предположим, что произведение 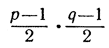четное. Тогда q есть вычет р в том и только в том случае, если р есть вычет q.

2) Предположим, напротив, что указанное произведение нечетное. Тогда ситуация резко меняется: q есть вычет р, если р есть невычет q, и наоборот.

Первое строгое доказательство закона взаимности, долгое время остававшегося гипотезой, данное Гауссом еще в молодости, явилось одним из крупных его достижений. Доказательство Гаусса никоим образом нельзя назвать простым, и в наше время провести доказательство закона взаимности стоит известного труда, хотя количество различных опубликованных доказательств очень велико. Истинный смысл закона взаимности вскрылся лишь в недавнее время - в связи с новейшим развитием алгебраической теории чисел.

В качестве примера, иллюстрирующего распределение квадратических вычетов, возьмем р = 7. Так как по модулю 7

0² = 0,

1² = 1,

2² = 4,

3² = 2,

4² = 2,

5² = 4,

6² = 1

и так как дальнейшие квадраты повторяют эту последовательность, то квадратическими вычетами числа 7 являются числа, сравнимые с 1, 2 и 4, а невычетами - числа, сравнимые с 3, 5 и 6. В общем случае квадратические вычеты р составляются из чисел, сравнимых с числами 1², 2², ..., (р - 1)². Но эти последние попарно сравнимы, так как

Действительно, (р - х)² = р² - 2рх + х² ≡ х² (mod p). Значит, половина чисел 1, 2, ..., р-1 представляет собой квадратические вычеты числа р, а другая половина - невычеты.

Чтобы дать иллюстрацию также и закону взаимности, положим p = 5, q = 11. Так как 11 = 1² (mod 5), то 11 есть квадратический вычет по модулю 5, и так как, кроме того, произведение 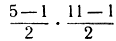четное, то согласно закону взаимности 5 должно быть также квадратическим вычетом по модулю 11; и в самом деле, мы видим, что 5 ≡ 4² (mod 11). С другой стороны, положим р = 7, q = 11. Гогда произведение 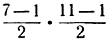нечетное, и, в этом случае 11 есть вычет по модулю 7 (так как 11 ≡ 2² (mod 7)), а 7 - невычет по модулю 11.

Упражнения. 1) 6² = 36 ≡ 13 (mod 23). Является ли 23 квадратическим вычетом по модулю 13?

2) Мы видели, что х² ≡ (р - х)² (mod р). Покажите, что иного вида сравнений между числами 1², 2², 3², ..., (р - 1)² быть не может.