2. Теорема Ферма

В XVII столетии Ферма, основатель современной теории чисел, открыл чрезвычайно важную теорему. Если р - простое число, не делящее целого числа а, то

Другими словами, (р - 1)-я степень а при делении на р дает остаток 1.

Некоторые из ранее произведенных нами вычислений подтверждают эту теорему: так, мы видим, что 10⁶ ≡ 1 (mod 7), 10² ≡ 1 (mod 3) и 10¹⁰ ≡ 1 (mod 11). Таким же образом легко проверить, что 2¹² ≡ 1 (mod 13) и 5¹⁰ ≡ 1 (mod 11). Для этой цели нет необходимости на самом деле вычислять столь высокие степени данных чисел; достаточно использовать мультипликативное свойство сравнений:

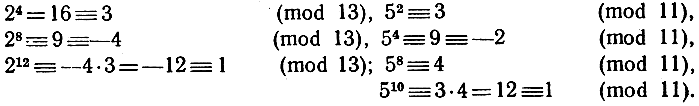
Обращаясь к доказательству теоремы Ферма, рассмотрим числа, кратные а:

Никакие два из этих чисел не могут быть между собой сравнимы по модулю р. В противном случае р должно было бы делить разность m_r - m_s = (r - s)а, где r, s была бы пара целых чисел, подчиненных ограничению 1≤r<s≤(р - 1). Но из закона 7) следует, что этого не может случиться: так как s - r меньше, чем р, то р не делит s - r; с другой стороны, по предположению, р не делит и а. Таким же образом мы убеждаемся, что ни одно из чисел m не сравнимо с нулем. Отсюда следует, что числа m₁, m₂, ..., m_p-1 соответственно сравнимы с числами 1,2, ...,р-1, взятыми в некоторой их перестановке. Дальше заключаем:

или же, полагая ради краткости К = 1*2*3*...*(р - 1),

Число К не делится на р, так как ни один из входящих в него множителей не делится на р, значит, согласно закону 7) (а^р-1 - 1) должно делиться на р, т. е.

Это и есть теорема Ферма.

Проверим эту теорему еще раз. Возьмем р = 23 и а = 5; тогда получаем по модулю 23 5² ≡ 2, 5⁴ ≡ 4, 5⁸ ≡ 16 ≡ - 7, 5¹⁶ ≡ 49 ≡ 3, 5²⁰ ≡ 12, 5²² ≡ 24 ≡ 1. Если возьмем а = 4 вместо 5, то будем иметь опять-таки по модулю 23 4² ≡ - 7, 4³ ≡ - 28 ≡ - 5, 4⁴ ≡ - 20 ≡ 3, 4⁸ ≡ 9, 4¹¹ ≡ - 45 ≡ 1, 4²² ≡ 1. В примере, где было взято а = 4, р = 23 (как и во многих иных), можно заметить, что не только (р - 1)-я степень, но и более низкая степень а уже оказывается сравнимой с единицей. Наименьшая такая степень - в нашем примере степень 11 - непременно есть делитель числа р - 1 (см. ниже, упражнение 3).

Упражнения.

1)С помощью подобных же вычислений проверить, что

2⁸ ≡ 1 (mod 17); 3⁸ ≡ - 1 (mod 17); 3¹⁴ ≡ -1 (mod 29); 2¹⁴ ≡ - 1 (mod 29); 4¹⁴ ≡ 1 (mod 29); 5¹⁴ ≡ 1 (mod 29).

2) Проверить теорему Ферма, взяв р = 5, 7, 11, 17 и 23 и придавая числу а различные значения.

3) Доказать общую теорему: Наименьшее число е, для которого а^е ≡ 1 (mod р), должно быть делителем р-1.

[Указание. Произвести деление р-1 на е, получая

где 0≤r<e, и дальше воспользоваться тем обстоятельством, что а^p-1 ≡ а^е ≡ 1 (mod р).]