
§ 2. Сравнения
1. Общие понятия
Всякий раз, как приходится говорить о делимости целых чисел на некоторое определенное число d, все рассуждения становятся яснее и проще, если пользоваться отношением сравнения, введенным Гауссом, и соответствующими обозначениями.
Чтобы ввести понятие сравнения, рассмотрим остатки, получающиеся при делении различных чисел, например, на 5. Мы получаем:
0 = 0*5 + 0
1 = 0*5 + 0
2 = 0*5 + 2
3 = 0*5 + 3
4 = 0*5 + 4
5 = 1*5 + 0
6 = 1*5 + 1
7 = 1*5 + 2
8 = 1*5 + 3
9 = 1*5 + 4
10 = 2*5 + 0
11 = 2*5 + 1
12 = 2*5 + 2
и т. д.
-1 = -1*5 + 4
-2 = -1*5 + 3
-3 = -1*5 + 2
-4 = -1*5 + 1
-5 = -1*5 + 0
-6 = -2*5 + 4
и т. д.
Заметим, что остатком при делении на 5 может быть только одно из чисел 0, 1, 2, 3, 4. Говорят, что два числа а и b сравнимы по модулю 5, если при делении на 5 они дают один и тот же остаток. Так, все числа 2, 7, 12, 17, 22, ..., -3, -8, -13, -18, ... сравнимы по модулю 5, так как при делении на 5 все они дают остаток 2. Вообще, говорят, что два числа а и b сравнимы по модулю d (где d - некоторое целое число), если при делении на d они дают один и тот же остаток; другими словами, если существует такое целое число n (положительное, отрицательное или нуль), что а - b = nd. Например, 27 и 15 сравнимы по модулю 4, так как 27 = 6*4 + 3, 15 = 3*4 + 3.
Для отношения сравнения введено специальное обозначение - если а и b сравнимы по модулю d, то пишут: a ≡ b (mod d). [Если же а не сравнимо с b по модулю d, то пишут: а 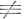 b (mod d).] Если ясно, какой модуль имеется в виду, то приписку "mod d" опускают.
b (mod d).] Если ясно, какой модуль имеется в виду, то приписку "mod d" опускают.
Сравнения часто встречаются в повседневной жизни. Например, часовая стрелка указывает время по модулю 12; автомобильный счетчик отмечает пройденные расстояния по модулю 100000 (миль или км).
Прежде чем перейти к более детальному рассмотрению сравнений и их свойств, пусть читатель проверит, что следующие утверждения в точности эквивалентны:
- а сравнимо с b по модулю d.
- а = b + nd, где n - целое.
- а - b делится на d.
Введенные Гауссом обозначения для сравнений подчеркивают то обстоятельство, что сравнения обладают многими свойствами обычных равенств. Напомним эти свойства:
1) Всегда а = а.
2) Если а - b, то b = а.
3) Если а = b и b = с, то а = с.
Кроме того, если а = а' и b = b', то
4) а + b = а' + b'.
5) а - b = а' - b'.
6) ab = a'b'.
Эти же свойства сохраняются, если отношение равенства а = b заменяется отношением сравнения a ≡ b (mod d). Именно:
1') Всегда а ≡ a (mod d).
2') Если a ≡ b (mod d), то b ≡ a (mod d).
3') Если a ≡ b (mod d) и b ≡ с (mod d), то а ≡ с (mod d).
(Проверьте!- это нетрудно.)
Точно так же, если а ≡ a' (mod d) и b ≡ b' (mod d), то
4') a + b ≡ а' + b' (mod d).
5') a - b ≡ a' - b' (mod d).
6') ab ≡ a'b'.(mod d).
Таким образом, сравнения по одному и тому же модулю можно складывать, вычитать и умножать. В самом деле, из
а = а' + rd, b = b' + sd
вытекает:
a + b = a' + b' + (r + s)d,
a - b = a' - b' + (r - s)d,
ab = а'b' + (a's + b'r + rsd)d,
что и приводит к нужным заключениям.

Рис. 6. Геометрическое представление целых чисел
Сравнения допускают великолепное геометрическое представление. Если хотят дать геометрическое представление целым числам, то обыкновенно выбирают прямолинейный отрезок единичной длины и затем откладывают кратные ему отрезки в обе стороны. Таким образом, для каждого целого числа получается соответствующая ему точка на прямой - числовой оси (рис. 6). Но если приходится иметь дело с числами по данному модулю d, два сравнимых числа - поскольку речь идет о делимости на d - рассматриваются как нечто неразличимое, так как они дают одни и те же остатки. Чтобы изобразить все это геометрически, возьмем окружность, разделенную на d равных частей. Всякое целое число при делении на d дает в качестве остатка одно из чисел 0, 1, 2, . . ., d-1: эти числа мы и расставим по окружности на равных расстояниях. Каждое число сравнимо с одним из этих чисел по модулю d и, следовательно, представляется соответствующей точкой; два числа сравнимы, если изображаются одной и той же точкой. Рис. 7 сделан для случая d = 6. Циферблат часов также может служить такой моделью.
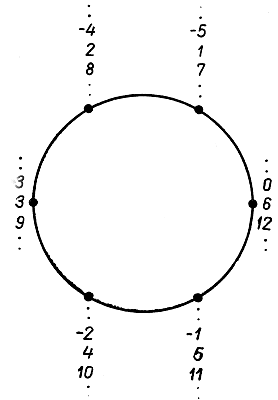
Рис. 7. Геометрическое представление целых чисел по модулю 6
В качестве примера применения мультипликативного свойства сравнений 60 определим остатки, получающиеся при делении на одно и то же число последовательных степеней числа 10. Так как 10 = - 1 + 11, то
10 = - 1 (mod 11).
Умножая многократно это сравнение само на себя, получаем дальше
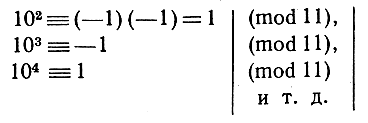
Отсюда можно заключить, что всякое целое число, запись по десятичной системе которого имеет вид:
z = а0 + a1*10 + a2*l02 + ... + аn*10n,
дает тот же остаток при делении на 11, что и сумма его цифр, взятая с чередующимися знаками
t = а0 - а1 + а2 - ...
В самом деле, мы имеем:
z - t = a1*11 + а2(102 - 1) + a3(103 + 1) + а4(104 - 1) + ...
Так как все выражения 102 - 1, 103 + 1, ... сравнимы с нулем по модулю 11, то z - t также сравнимо с нулем, и потому z при делении на 11 дает тот же остаток, что и t. В частности, число делится на 11, т. е. дает остаток 0 при делении, в том и только в том случае, если знакочередующаяся сумма его цифр делится на 11. Например, число z = 3 162 819 делится на 11, так как 3 - 1 + 6 - 2 + 8 - 1 + 9 = 22 делится на 11. Найти таким же образом правило делимости на 3 или на 9 еще проще, так как 10 ≡ 1 (mod 3 и 9), и потому 10n ≡ 1 (mod 3 и 9) при любом n. Отсюда следует, что число z делится на 3 и на 9 в том и только в том случае, если сумма его цифр
s = а0 + а1 + а2 + ... + аn
делится соответственно на 3 и на 9.
Если в качестве модуля возьмем 7, то получим
10 ≡ 3, 102 ≡ 2, 103 ≡ -1, 104 ≡ - 3, 105 ≡ -2, 106 ≡ 1.
Далее остатки повторяются. Таким образом, z делится на 7 в том и только в том случае, если выражение
r = а0 + 3a1 + 2а2 - а3 - 3а4 - 2а5 + a6 + 3а7 + ...
делится на 7.
Упражнение. Найти подобный же признак делимости на 13.
Складывая и умножая сравнения по определенному модулю, скажем d = 5, можно всегда обеспечить то, чтобы входящие числа не становились слишком большими, заменяя всякий раз встречающееся число одним из чисел
0, 1, 2, 3, 4,
а именно тем, с которым оно сравнимо. Так, вычисляя суммы и произведения различных чисел по модулю 5, нужно только пользоваться следующими таблицами сложения и умножения:
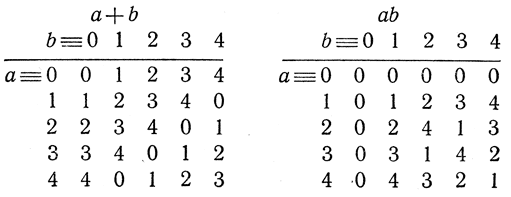
Из второй таблицы видно, что произведение ab сравнимо с нулем по модулю 5 только в том случае, если а или b≡ 0 (mod 5). Это наводит на мысль о существовании следующего общего закона:
7) ab ≡ 0 (mod d) только в том случае, если а ≡ 0 или b ≡ 0 (mod d), что является распространением хорошо известного свойства обыкновенного умножения:
ab = 0 только в том случае, если а = 0 или b = 0.
Но закон 7) действителен только при том условии, что модуль d есть простое число. Действительно, сравнение
ab ≡ 0 (mod d)
означает, что ab делится на d, а мы уже видели, что произведение ab делится на простое d в том и только в том случае, если один из множителей а или b делится на d, т. е. если
а ≡ 0 (mod d) или b ≡ 0 (mod d).
С другой стороны, закон теряет силу при d составном: можно тогда написать d = r*s, где оба множителя r и s меньше, чем d, так что
r 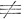 0 (mod d), s
0 (mod d), s 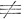 0 (mod d)
0 (mod d)
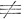 0 (mod d), s
0 (mod d), s 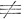 0 (mod d)
0 (mod d)и, однако,
rs = d ≡ 0 (mod d).
Например, 2 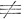 0 (mod 6) и 3
0 (mod 6) и 3 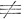 0 (mod 6), но 2*3 = 6 ≡ 0 (mod 6).
0 (mod 6), но 2*3 = 6 ≡ 0 (mod 6).
Упражнение. Покажите, что имеет место следующее правило сокращения на простой множитель.
Если ab ≡ ас и a 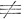 0, то b ≡ с.
0, то b ≡ с.
Упражнения.
1) С каким числом в пределах от 0 до 6 включительно сравнимо число 11*18*2322*13*19 по модулю 7?
2) С каким числом в пределах от 0 до 12 включительно сравнимо число 3*7*11*17*19*23*29*113 по модулю 13?
3) С каким числом в пределах от 0 до 4 включительно сравнима сумма 1 + 2 + 22 + ... + 219 по модулю 5?
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'