§ 4. Алгорифм Евклида

1. Общая теория

Читатель прекрасно знаком с обычной процедурой "длинного" деления одного целого числа а на другое число b и знает, что эту процедуру можно продолжать до тех пор, пока остаток не станет меньше, чем делитель. Так, если а = 648 и b = 7, то мы получаем частное q = 92 и остаток r = 4.

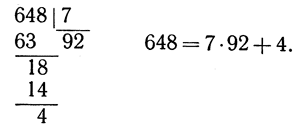
По этому поводу можно сформулировать следующую общую теорему: если a и b - целые числа, причем b отлично от нуля, то можно всегда найти такое целое число q, что

где r есть целое число, удовлетворяющее неравенству 0≤r<b.

Докажем эту теорему независимо от процедуры длинного деления. Достаточно заметить, что число а или само есть кратное числа b, или же лежит между двумя последовательными кратными b:

В первом случае равенство (1) оправдывается, причем r = 0. Во втором случае из первого неравенства вытекает, что

а из второго, что

так что число r в этом случае удовлетворяет условию 0<r<b.

Из отмеченного обстоятельства можно вывести большое число различных важных следствий. Первое из них - это метод для нахождения общего наибольшего делителя двух целых чисел.

Пусть а и b - два каких-то целых числа, не равных одновременно нулю; рассмотрим совокупность всех чисел, на которые делятся и а и b. Эта совокупность, несомненно, конечная, так как если, например, а≠ 0, то никакое число, большее чем а, не может быть делителем а. Отсюда следует, что число общих делителей а и b конечно: пусть через d обозначен наибольший из них. Число d называется общим наибольшим делителем а и b, и мы условимся обозначать его d = (а, b). Так, если а = 8, b = 12, то непосредственная проверка показывает, что (8, 12) = 4; если а - 5, b = 9, то мы точно так же получаем (5,9) = 1. Если а и b - достаточно большие числа, например, а = 1804, b = 328, то попытки найти общий наибольший делитель с помощью непосредственных проб довольно утомительны. Короткий и вполне надежный метод вытекает из алгорифма Евклида. (Алгорифмом называют всякий систематизированный прием вычисления.) Он основан на том обстоятельстве, что из соотношения вида

необходимо следует, что

В самом деле, всякое число u, которое одновременно делит и а и b

делит также и r, так как r = а - bq = su - qtu = (s - qt)u; и обратно, всякое число и, которое одновременно делит b и r

делит также и а, так как а = bq + r = s'vq + t'v = (s'q + t')v. Значит, каждый общий делитель а и b есть вместе с тем общий делитель b и r, и обратно. Но раз совокупность всех общих делителей а и b совпадает с совокупностью всех общих делителей b и г, то ясно, что общий наибольший делитель а и b должен совпадать с общим наибольшим делителем b и r. А это и выражено равенством (3). Мы сейчас убедимся в полезности установленного обстоятельства.

Для этого вернемся к примеру нахождения общего наибольшего делителя чисел 1804 и 328. Обыкновенное "длинное" деление

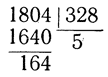
приводит нас к заключению, что

Отсюда в силу (3) следует, что

Заметим, что задача вычисления общего наибольшего делителя (1804, 328) заменена теперь аналогичной задачей, но зависящей от меньших чисел. Можно продолжать эту процедуру. Так как

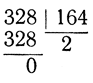
то мы получаем дальше 328 = 2*164 + 0, так что (328, 164) - (164,0) = 164. Значит, (1804, 328) = (328, 164) = (164,0) = 164, и общий наибольший делитель найден.

Эта самая процедура нахождения общего наибольшего делителя двух чисел в геометрической форме описана в "Началах" Евклида. Мы дадим ее общее описание в арифметической форме, исходя из произвольных целых чисел а и b, которые оба одновременно не равны нулю.

Так как сразу ясно, что (а,0) = а, то можно допустить, что b≠0. Последовательные деления приводят нас к цепи равенств:

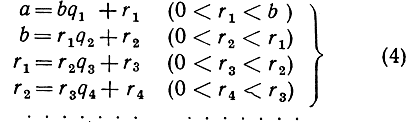
Деление продолжается, пока какой-нибудь из остатков r₁, r₂, r₃,... не обратится в нуль. Рассматривая неравенства, выписанные справа, мы видим, что последовательно получаемые остатки образуют убывающую последовательность положительных чисел:

Отсюда ясно, что после конечного числа делений (нужно сделать не более b операций, но часто гораздо меньше, так как разности между соседними r обыкновенно превышают единицу) должен получиться остаток 0:

Как только это получится, мы можем утверждать, что (а, b) = r_n; другими словами, общий наибольший делитель (а, b) равен последнему остатку в последовательности (5). Это следует из повторного применения равенства (3) к соотношениям (4); в самом деле, из этих соотношений следует:

Упражнение. Выполните алгорифм Евклида с целью нахождения общего наибольшего делителя: а) 187; 77; Ь) 105; 385; с) 245; 193.

Из равенств (4) можно вывести одно o чрезвычайно важное свойство общего наибольшего делителя (а, b): Если d = (а, b), то можно найти такие целые положительные или отрицательные числа k и l, что

Чтобы убедиться в этом, рассмотрим последовательные остатки (5). Первое из равенств (4) нам дает

так что r₁ может быть записано в форме k₁a + l₁b (в данном случае k₁ = 1, l = -q₁). Из следующего равенства получается: r₂ = b - q₂r₁ = b - q₂(k₁a + l₁b) = (-q₂k₁)a +

Очевидно, такое же рассуждение можно по очереди применить ко всем остаткам r₃, r₄,..., пока не придем к представлению

которое мы и желали получить.

В качестве примера рассмотрим алгорифм Евклида в применении к нахождению (61, 24): общий наибольший делитель есть 1, и интересующее нас представление числа 1 получается из равенств

Первое из этих равенств дает

13 = 61 - 2*24,

второе -

третье -

и, наконец, четвертое -