7. Дальнейшие замечания по поводу метода математической индукции

Принцип математической индукции может быть несколько обобщен следующим образом: "Если имеется последовательность утверждений A_s, A_s+1, A_s+2, ..., где s - некоторое положительное число, и если:

a) при всяком значении r≥s справедливость А_r+1 следует из справедливости А_r и

b) известно, что A_s справедливо,

то все утверждения A_s, A_s+1, A_s+2, ... справедливы". Иначе говоря, А_n "справедливо при любом n≥s". То же самое рассуждение, которое привело нас к обыкновенному принципу математической индукции, пригодно и в данном случае, только последовательность 1, 2, 3, ... заменяется на этот раз подобной ей последовательностью s, s+1, s+2, s+3, ... .

Пользуясь принципом индукции в этой форме, мы можем несколько усилить неравенство на стр. 40, исключая возможность знака равенства. Именно: каково бы ни было р≠0 и >- 1 и каково бы ни было целое число n≥2, имеет место неравенство

Доказательство предоставляется читателю.

С принципом математической индукции тесно связан "принцип наименьшего целого числа", утверждающий, что во всяком непустом множестве С натуральных чисел имеется наименьшее число. Множество С может быть конечным, как например множество 1, 2, 3, 4, 5, или бесконечным, как например множество всех четных чисел 2, 4, 6, 8, 10, ... . Множество называется пустым, если оно не содержит ни одного элемента; примером пустого множества может служить множество всех кругов, одновременно являющихся прямыми линиями, или множество натуральных чисел n, удовлетворяющих - соотношению n>n. По понятным причинам мы оговариваем в формулировке "принципа наименьшего целого числа", что пустые множества исключаются. Всякое непустое множество С целых чисел непременно содержит хоть одно число, например n, и тогда наименьшее из чисел 1, 2, 3, ..., n, принадлежащее множеству С, есть наименьшее целое число множества.

Чтобы уяснить значение этого принципа, следует указать на то обстоятельство, что он, вообще говоря, неверен для множеств, состоящих из нецелых чисел; например, множество положительных дробных чисел 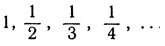не содержит наименьшего числа.

С чисто логической точки зрения небезынтересно отметить то обстоятельство, что с помощью принципа наименьшего целого числа принцип математической индукции доказывается как теорема. В самом деле, пусть имеется последовательность таких утверждений А₁, A₂, А₃, ..., что:

a) при любом r справедливость А_r+1 вытекает из справедливости А_r,

b) известно, что А₁ справедливо.

Мы докажем, что предположения о том, что хоть одно из утверждений А несправедливо, придется отбросить. Действительно, если бы хоть одно из утверждений А было неверным, то множество всех натуральных чисел n, для которых А_n неверно, не было бы пустым. Тогда согласно принципу наименьшего целого числа оно содержало бы наименьшее число р, которое вследствие b) должно было бы быть больше чем 1. Но тогда Ар было бы неверно, а А_р-1 верно. Это противоречит условию а).

Подчеркнем еще раз, что принцип математической индукции резко отличается от эмпирической индукции, свойственной естественным наукам. Подтверждение общего закона на конечном числе случаев (как бы это число ни было велико) никоим образом не представляет собой доказательства в математическом смысле, даже если неизвестно ни одного исключения. При таких обстоятельствах рассматриваемое утверждение, или "закон", есть не что иное, как вполне разумная гипотеза, которую могут видоизменить результаты будущих экспериментов. В математике "закон" может считаться доказанным только тогда, когда он выведен как неизбежное логическое следствие из предпосылок, признаваемых справедливыми. Существует немало примеров математических утверждений, которые были проверены и оправдывались во всех до настоящего времени рассмотренных частных случаях, но для которых еще не было найдено общего доказательства (см. пример на стр.55). Можно подозревать, что теорема справедлива во всей общности, если она подтверждается на большом числе примеров, и тогда есть основание пытаться доказать ее с помощью математической индукции. Если попытка удается, то тем самым справедливость теоремы устанавливается; в противном случае вопрос о том, верна или неверна теорема, остается открытым, и она может быть доказана или опровергнута когда-нибудь в будущем уже иными методами.

Применяя принцип математической индукции, необходимо всегда тщательно следить за тем, чтобы условия а) и b) были действительно выполнены. Иначе можно иной раз прийти и к абсурду. Мы предлагаем читателю разобраться в следующем софизме. Мы "докажем" сейчас, что любые два целых положительных числа равны между собой; например, 5 = 10. Начнем с определения. Если а и b - два неравных между собой целых положительных числа, то через max (а, b) будем обозначать а или b, смотря по тому, какое из чисел больше: а или b; если же а = b, то положим max (а, b) = а = b. Так, max (3, 5) = max (5, 3) = 5, тогда как max (4, 4) - 4. Далее, через А_n обозначим следующее утверждение: "Если а и b - два таких целых положительных числа, что max (а, b) = n, то а = b".

a) Предположим, что А_r верно. Пусть а и b - два таких целых положительных числа, что max (а, b) = r + 1. Рассмотрим числа

тогда max (α, β) = r. В таком случае α = β, так как А_r верно. Но отсюда следует, что а = b; значит, верно и А_r+1.

b) A₁( очевидно, верно, так как если max (а, b) = 1, то а и b (по предположению - целые положительные числа) должны быть каждое в отдельности равны 1.

Итак, по принципу математической индукции А_n верно при любом n.

Пусть теперь а и b - два произвольных целых положительных числа; положим max (а, b) = r. Было показано, что А_n верно при любом n; значит, в частности, верно А_r. Следовательно, а = b.