*6. Биномиальная теорема

Часто бывает нужно написать в раскрытом виде выражение для n-й степени бинома (а + b)ⁿ. Непосредственное вычисление показывает, что

при n = 1 (а + b)¹ = а + b,

при n = 2 (а + b)² = (а + b)(а + b) = а(а + b) + b(а + b) = а² + 2ab + b²,

при n = 3 (а + b)³ = (а + b)(а + b)² = а(а² + 2аb + b²) + b(а² + 2аb + b²) = а³ + 3а²b + 3аb² + b³

и так далее. Но какой общий закон скрывается за словами "и так далее"? Проанализируем процесс вычисления (а + b)². Так как (а + b)² = (а + b)(а + b), то мы получили выражение для (а + b)², умножая каждый член выражения а + b на а, затем на b и складывая то, что получилось. Ту же процедуру пришлось применить при вычислении (а + b)³ = (а + b)(а + b)². Так же точно вычисляются (а + b)⁴, (а + b)⁵ и так далее до бесконечности. Выражение для (а + b)ⁿ мы получим, умножая выражение (а + b)^n-1 сначала на а, потом на b, затем складывая то, что получится. Это приводит к следующей диаграмме:

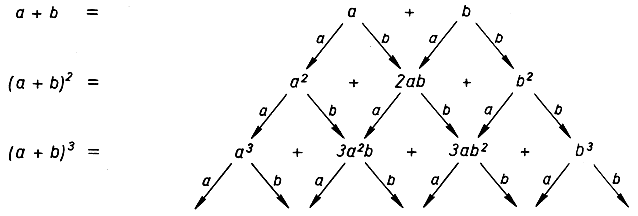
позволяющей сразу разобраться в общем законе составления коэффициентов в разложении (а + b)ⁿ. Мы строим треугольную схему из натуральных чисел, начиная с коэффициентов 1, 1 двучлена а + b таким образом, что каждое число в треугольнике является суммой двух чисел, стоящих над ним в предыдущей строке (слева и справа). Такая схема известна под названием треугольника Паскаля.

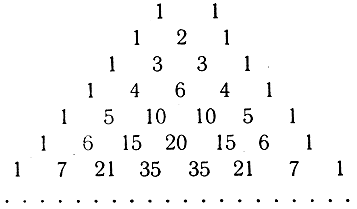
Коэффициенты в разложении (а + b)ⁿ по убывающим степеням а и возрастающим степеням b стоят в n-й строке этой схемы.

Так, например,

С помощью очень сжатых обозначений, использующих нижние и верхние значки (индексы), запишем числа, стоящие в n-й строке треугольника Паскаля, следующим образом:

Тогда общей формуле для разложения (а + b)ⁿ можно придать вид:

Согласно закону, лежащему в основе построения треугольника Паскаля, мы имеем соотношение:

В качестве упражнения читатель, имеющий уже некоторый опыт в применении математической индукции, может воспользоваться этим принципом (и очевидными равенствами C₀¹ = C₁¹ = 1) для доказательства общей формулы

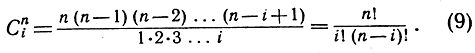
[При любом целом положительном значении n символ n! (читается "n-факториал") обозначает произведение n первых натуральных чисел: n! = 1*2* ... *n. Удобно также положить по определению 0! = 1, чтобы формула (9) оправдывалась также и при i, равном 0 или n].

Выводу этой формулы для коэффициентов биномиального разложения иногда дается наименование биномиальной теоремы (см. также стр. 514).

Упражнения. Доказать с помощью метода математической индукции следующие равенства:

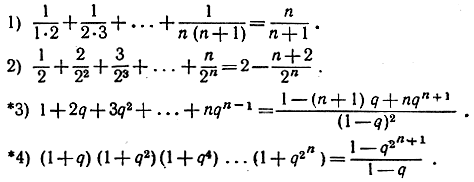
Найти сумму следующих геометрических прогрессий:

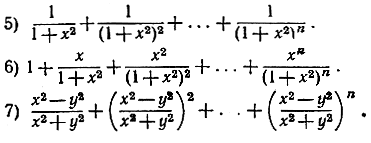
Пользуясь формулами (4) и (5), доказать:

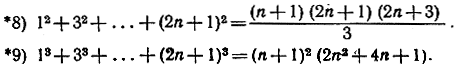
10) То же самое доказать непосредственно методом математической индукции.