4. Сумма n первых квадратов

Следующее интересное применение принципа математической индукции относится к сумме n первых квадратов. Путем проб мы устанавливаем (по крайней мере для нескольких небольших значений n), что

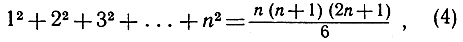
после чего естественно высказать в виде догадки утверждение, что эта замечательная формула справедлива при всех целых положительных значениях n. Чтобы доказать это, воспользуемся опять методом математической индукции. Заметим прежде всего, что если утверждение A_n, которое заключается как раз в соотношении (4), справедливо при n = r, так что

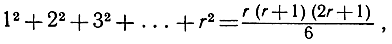
то, прибавляя к обеим частям по (r+1)², мы получаем:

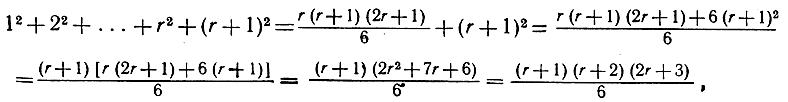
а это и есть утверждение A_r+1, так как оно получается из соотношения (4) посредством подстановки r+1 вместо n. Чтобы закончить доказательство, достаточно обратить внимание на то, что утверждение А₁, которое сводится к равенству

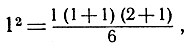
справедливо. Итак, соотношение (4) верно при всех значениях n.

Подобного же рода формулы можно написать для сумм третьих и четвертых степеней, вообще для сумм вида 1^k + 2^k + 3^k + ... + n^k, где k - произвольное целое положительное число. В качестве упражнения читатель может доказать с помощью математической индукции формулу

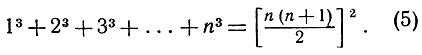
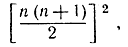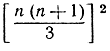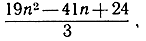Необходимо заметить в заключение, что, хотя принципа математической индукции совершенно достаточно для того, чтобы доказать формулу (5) - раз она уже написана, однако доказательство не дает решительно никаких указаний, как прийти к самой этой формуле: почему именно нужно догадываться, что сумма n первых кубов равна выражению а не какому-нибудь иному в таком же роде, например или и т. д. Выбор велик! Тот факт, что доказательство теоремы заключается в применении таких-то простых логических правил, не оказывает ни малейшего влияния на творческое начало в математике, роль которого - делать выбор из бесконечного множества возникающих возможностей. Вопрос о том, как возникает гипотеза (5), принадлежит к той области, в которой нет никаких общих правил; здесь делают свое дело эксперимент, аналогия, конструктивная индукция. Раз только правильная гипотеза сформулирована, принципа математической индукции часто бывает достаточно, чтобы теорема была доказана. Но так как само такое доказательство никак не указывает пути к открытию, то его лучше было бы называть проверкой.