
3. Геометрическая прогрессия
Таким же образом можно рассуждать и по поводу геометрической прогрессии (в общем виде). Мы покажем, что, каково бы ни было n,
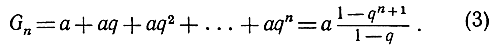
(Мы предполагаем, что q ≠ 0 иначе правая часть (3) лишена смысла.) Наше утверждение, несомненно, справедливо при n = 1, так как в этом случае
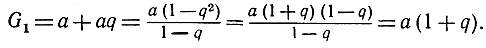
И если мы допустим, что
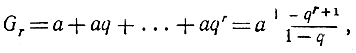
то, как следствие, отсюда немедленно вытекает:
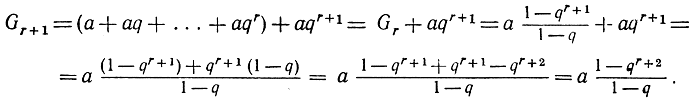
Но это как раз и есть утверждение (3) при n = r + 1. Доказательство закончено.
В элементарных учебниках дается другое доказательство. Положим;
Gn = a + aq + ... + aqn.
Умножая обе части на q, получим:
qGn = aq + aq2 + ... + aqn+1.
Вычитая затем последнее равенство из предпоследнего, получаем далее:
Gn - qGn = a - aqn+1,
(1-q)Gn = a(1 - qn+1),
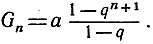
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'