2. Арифметическая прогрессия

Каково бы ни было значение n, сумма 1 + 2 + 3 + ... + n первых n натуральных чисел равна 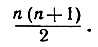Чтобы доказать эту теорему посредством математической индукции, мы должны для произвольного значения n установить справедливость соотношения А_n:

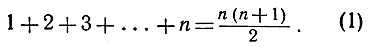
а) Если r - некоторое натуральное число и если известно, что утверждение А_r справедливо, т. е. если известно, что

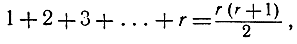
то, прибавляя к обеим частям последнего равенства по r+1, мы получаем:

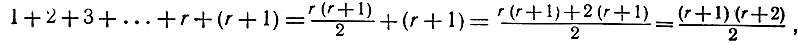
а это как раз и есть утверждение А_r+1.

b) Утверждение А₁, очевидно, справедливо, так как 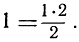Итак, по принципу математической индукции утверждение А_n справедливо при любом n, что и требовалось доказать.

Обыкновенно эту теорему доказывают иным способом. Пишут сумму 1 + 2 + 3 + ... + n в двух видах:

и

Складывая, мы видим, что числа, стоящие на одной вертикали, вместе составляют n+1, и так как вертикалей всего имеется n, то отсюда следует, что

и остается еще разделить на 2.

Из формулы (1) сразу же вытекает общая формула для суммы (n+1) первых членов любой арифметической прогрессии:

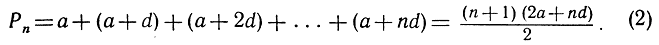
В самом деле,

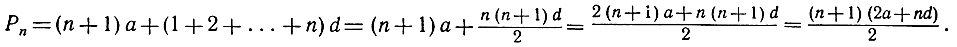
В случае, когда a = 0, d = 1, последнее соотношение превращается в соотношение (1).