3. Арифметические действия в недесятичных системах счисления

Исключительная роль десятка восходит к истокам цивилизации и без всякого сомнения связана со счетом по пальцам на двух руках. Но наименования числительных в разных языках указывают и на наличие (в былые времена) иных систем счисления, именно с основаниями двадцать и двенадцать. В английском и немецком языках слова, обозначающие 11 и 12, построены не по десятичному принципу, сочетающему десятки с единицами: они лингвистически независимы от слов, обозначающих число 10. Во французском языке слова, обозначающие 20 и 80, позволяют предполагать первоначальное существование системы с основанием 20, используемой для тех или иных надобностей. В датском языке слово halvfirsinds-tyve, обозначающее 70, буквально переводится "полпути от трижды двадцать до четырежды двадцать". Вавилонские астрономы пользовались системой, являвшейся отчасти шестидесятеричной (с основанием 60), и именно в этом обстоятельстве следует искать объяснение того факта, что час и угловой градус подразделены на 60 минут.

В недесятичных системах счисления правила арифметики, конечно, те же самые, но таблицы сложения и умножения однозначных чисел отличны от наших десятичных. Будучи приучены к десятичной системе и связаны наименованиями числительных в нашем языке, мы, если попытаемся считать по иным системам, сначала испытаем известное неудобство. Попробуем поупражняться в умножении по семеричной системе. Прежде чем приступить к этому, рекомендуется выписать две таблички, которыми придется пользоваться.

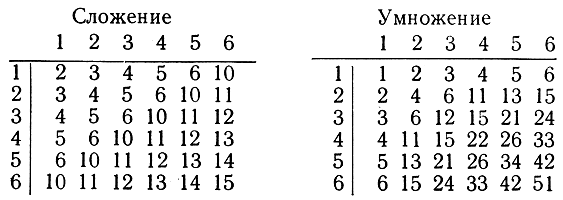
Станем теперь умножать 265 на 24, причем эти числа предполагаются написанными в семеричной системе. (Если написать числа по десятичной системе, то речь идет об умножении 145 на 18.) Начнем с умножения 5 на 4, что, как показывает таблица умножения, дает 26.

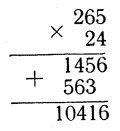
Мы пишем 6 на месте единицы, затем переносим двойку в следующий разряд. Далее, находим, что 4*6 = 33 и что 33 + 2 = 35. Пишем в произведении 5 и продолжаем таким же образом, пока умножение не закончится. При сложении чисел 1456 и 5630 на месте единиц получаем 6 + 0 = 6, затем на месте семерок 5 + 3 = 11. Пишем 1 и 1 переносим на место "сорокадевяток", где получается 1 + 6 + 4 = 14. Окончательный результат: 265*24 = 10 416.

Для проверки проделаем то же действие в десятичной системе. Чтобы переписать число 10 416 по десятичной системе, придется найти степени 7 вплоть до четвертой: 7² = 49, 7³ = 343, 7⁴ = 2401. Отсюда следует, что 10 416 = 2401 + 4*49 + 7 + 6, причем правая часть равенства записана уже по десятичной системе. Складывая числа, мы находим, что число 10 416, записанное по семеричной системе, равно числу 2610, записанному по десятичной. Умножим теперь 145 на 18 в десятичной системе: получается как раз 2610.

Упражнения.

1. Составьте таблицы сложения и умножения в двенадцатеричной системе и проделайте несколько примеров вроде приведенного выше.
2. Напишите "тридцать" и "сто тридцать три" в системах с основаниями 7, 11, 12.
3. Что обозначают символы 11 111 и 21 212 в этих системах?
4. Составьте таблицы сложения и умножения для систем с основаниями 5, 11, 13.

С теоретической точки зрения система, построенная по позиционному принципу с основанием 2, выделяется в том смысле, что это основание - наименьшее из возможных, В этой двоичной (диадической, бинарной) системе имеются лишь две цифры: 0 и 1; всякое иное число записывается как комбинация этих символов. Таблицы сложения и умножения сводятся к двум правилам: 1 + 1 = 10 и 1*1 = 1. Но непрактичность такой системы достаточно очевидна^*: чтобы изобразить уже небольшие числа, нужны длинные выражения. Так, число "семьдесят девять", которое представляется в виде 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 1*2 + 1, записывается в двоичной системе как 1 001 111.

^* (Со времени написания книги (1941 г.; последнее английское издание, которым мы располагали, вышло в 1948 г.) столь "непрактичная" для обычного счета двоичная система получила широкие и достаточно общеизвестные применения в машинной математике (идея которых - "кодирование" любого текста с помощью алфавита из двух знаков - предугадывается в приводимой ниже фразе Лапласа о Лейбнице).)

Чтобы проиллюстрировать, насколько просто производится умножение в двоичной системе, перемножим числа семь и пять, которые записываются соответственно в виде 111 и 101. Принимая во внимание, что в этой системе 1 + 1 = 10, мы пишем:

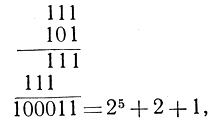
и в итоге, как и следовало ожидать, получается тридцать пять.

Готфрид Вильгельм Лейбниц (1646-1716), один из величайших умов своего времени, расценивал двоичную систему чрезвычайно высоко. Вот что говорит по этому поводу Лаплас: "В своей бинарной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль - небытие, и что Высшее Существо создает все сущее из небытия точно таким же образом, как единица и нуль в его системе выражают все числа".

Упражнение. Исследуйте в общем виде вопрос о представлении чисел в системе с основанием а. Чтобы называть числа в этой системе, нужны наименования для однозначных чисел 0, 1, ..., а-1 и для различных степеней а: а, а², а³, ... . Сколько именно числительных потребуется, чтобы назвать все числа до одной тысячи в системах с основанием а = 2, 3, 4, 5, ..., 15? Каково должно быть основание а, чтобы число этих имен числительных было наименьшим? (Примеры: если а= 10, то нужно десять числительных для однозначных чисел, затем еще три числительных, обозначающих 10, 100 и 1000, всего 13. При а - 20 нужно двадцать числительных для однозначных чисел и еще числительные для 20 и 400, всего 22. При а = 100 понадобится 101 числительное.)