2. Представление целых чисел с помощью письменных знаков (нумерация)

Необходимо очень тщательно делать различие между целым числом и тем символом (например, 5, V и т. п.), которым пользуются для его письменного воспроизведения. В нашей десятичной системе нуль и девять целых натуральных чисел обозначаются цифрами 0, 1, 2, 3, . . ., 9. Числа большей величины, как, скажем, "триста семьдесят два", представляются в виде

и в десятичной системе записываются символом 372. Существенно в данном случае то, что смысл каждой из цифр 3,7,2 зависит от ее положения - от того, стоит ли она на месте единиц, десятков или сотен. Используя "поместное значение" цифр (позиционный принцип), мы имеем возможность изобразить любое натуральное число с помощью всего лишь десяти цифр в их различных комбинациях. Общее правило такого изображения дается схемой, которая иллюстрируется примером

где а, b, с, d представляют собой целые числа в пределах от нуля до девяти. Число z в этом случае сокращенно обозначается символом

Заметим, между прочим, что коэффициенты d, c, b, а являются не чем иным, как остатками при последовательном делении числа z на 10. Так, например,

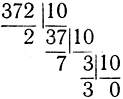
С помощью написанного выше выражения для числа z можно изображать только те числа, которые меньше десяти тысяч, так как числа, большие чем десять тысяч, требуют пяти или большего числа цифр. Если z есть число, заключенное между десятью тысячами и ста тысячами, то его можно представить в виде

и записать символически как abcde. Подобное же утверждение справедливо относительно чисел, заключенных между ста тысячами и одним миллионом, и т. д. Чрезвычайно важно располагать способом, позволяющим высказать результат, к которому мы приходим, во всей его общности посредством одной-единственной формулы. Мы можем добиться этой цели, если обозначим различные коэффициенты е, d, с, . . . одной и той же буквой а с различными значками (индексами) а₀, а₁, а₂, . . ., а то обстоятельство, что степени числа 10 могут быть сколь угодно большими, выразим тем, что высшую степень числа 10 обозначим не 10³ или 10⁴, как в предыдущих примерах, а станем писать 10ⁿ, понимая под n совершенно произвольное натуральнее число. В таком случае любое целое число z в десятичной системе может быть представлено в виде

и записано посредством символа

Как и в частном, рассмотренном выше примере, мы обнаруживаем, что а₀, а₁, а₂, ..., а_n являются остатками при последовательном делении z на 10.

В десятичной системе число "десять" играет особую роль как "основание" системы. Тот, кому приходится встречаться лишь с практическими вычислениями, может не отдавать себе отчета в том, что такое выделение числа "десять" не является существенным и что роль основания способно было бы играть любое целое число, большее единицы. Например, был,а бы вполне возможна семеричная система с основанием семь. В такой системе целое число представлялось бы в виде

где коэффициенты b обозначают числа в пределах от нуля до шести, и оно записывалось бы посредством символа

Так, число "сто девять" в семеричной системе обозначалось бы символом 214, потому что

В качестве упражнения читатель может вывести общее правило для перехода от основания 10 к любому основанию В: нужно выполнять последовательные деления на В, начиная с данного числа z остатки и будут "цифрами" при записи числа в системе с основанием В. Например,

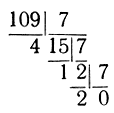
109 (в десятичной системе) = 214 (в семеричной системе).

Естественно, возникает вопрос: не был ли бы особенно желательным выбор какого-либо специального числа в качестве основания системы счисления? Мы увидим дальше, что слишком маленькое основание должно было бы вызвать кое-какие неудобства; с другой стороны, слишком большое основание потребовало бы заучивания многих цифр и знания расширенной таблицы умножения. Высказывались соображения в пользу системы с основанием 12 ("двенадцатеричной"): указывалось, что 12 делится без остатка на два, на три, на четыре и на шесть, и потому вычисления, связанные с делениями и дробями, при основании 12 были бы несколько проще. Чтобы написать произвольное число в двенадцатеричной системе, понадобились бы две лишние цифры - для обозначения чисел "десять" и "одиннадцать". Пусть α обозначало бы десять, а β - одиннадцать. Тогда в двенадцатеричной системе "двенадцать" пришлось бы написать в виде 10, "двадцать два" - в виде 1α, "двадцать три" - в виде 1β, а "сто тридцать один" - в виде αβ.

Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерийцам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. Более древние системы нумерации были построены исключительно на аддитивном принципе^*. Так, в римской нумерации CXVIII обозначает "сто + десять + пять + один + один + + один". Египетская, еврейская и греческая системы были на том же уровне. Неудобством чисто аддитивной системы является то обстоятельство, что с увеличением изображаемых чисел требуется неограниченное число новых символов. Но главнейшим недостатком древних систем (вроде римской) было то, что сама процедура счета была очень трудна: даже самые простые задачи могли решать только специалисты-профессионалы. Совсем иначе обстоит дело с распространенной в наше время индусской "позиционной" системой. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших ее у мусульман. Позиционная система обладает тем чрезвычайно выгодным свойством, что все числа, и малые и большие, могут быть записаны с помощью небольшого числа различных символов; в десятичной системе таковыми являются "арабские цифры" 0, 1, 2, ..., 9. Не меньшее значение имеет и легкость счета в этой системе. Правила действий с числами, записываемыми по позиционному принципу, могут быть резюмированы в виде таблиц сложения и умножения и могут быть раз навсегда выучены на память. Старинному методу счета, которым раньше владели лишь немногие избранные, теперь обучают разве лишь в начальных школах. В истории культуры найдется немного примеров того, чтобы научный прогресс оказал на практическую жизнь столь глубокое, столь облегчающее влияние.

^* (На самом деле элементы "позиционности" есть и в римской нумерации, во всяком случае, порядок расположения "разрядов" играет роль; так, VI = V + I, но IV = V - I, LX = L + X, но XL = L - X и т. п.)