Глава I. Натуральные числа

Введение

Число - это основное понятие современной математики. Но что такое число? Если мы говорим, что 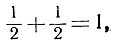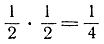или что (-1)*(-1) = 1, то какой смысл вкладывается в эти утверждения? В школе мы изучаем технику действий с дробями и с отрицательными числами, но, чтобы приобрести подлинное понимание того, как устроена система чисел, недостаточно ограничиваться элементарными сведениями и нужно пойти несколько дальше. Греки в древнее время в основу созданной ими математики положили геометрические концепции точки и прямой; руководящим принципом современной математики стало сведение в конечном счете всех утверждений к утверждениям, касающимся натуральных чисел 1, 2, 3,... . "Бог создал натуральные числа, все прочее - творение человека". Этими словами Леопольд Кронекер (1823-1891) определил тот прочный фундамент, на котором может быть построено здание математики.

Числа служат для того, чтобы считать объекты, входящие в состав тех или иных объединений или собраний. Числа решительно никак не связаны с индивидуальной характеристикой считаемых объектов. Так, число "шесть" есть результат абстрагирования, производимого при рассмотрении всевозможных совокупностей, состоящих из шести предметов: оно нисколько не зависит ни от специфических свойств этих объектов, ни от употребляемых символов (обозначений). Но абстрактный характер идеи числа становится ясным только на очень высокой ступени интеллектуального развития. В глазах детей числа всегда остаются соединенными с самими осязаемыми объектами - допустим, пальцами или камешками; в языках народов числа также трактуются конкретно: для обозначения предметов различных типов употребляются различные сочетания числительных.

Мы воспользуемся тем, что математик (как таковой) не обязан заниматься философской проблемой перехода от совокупностей конкретных предметов к абстрактному понятию числа. Мы примем поэтому натуральные числа как данные вместе с двумя основными операциями, над ними совершаемыми: сложением и умножением.