
§ 10. Ветвящиеся процессы. Дифференциальное уравнение для производящей функции. Эффекты вырождения и взрыва
1. Предположим, что имеется некоторая совокупность частиц, каждая из которых с течением времени превращается в частицы такого же типа, причем этот процесс "размножения" обладает следующим свойством: каждая из исходных частиц через время t независимо друг от друга и от обстоятельств, предшествующих исходному моменту, с одинаковой для всех частиц вероятностью pk (t) порождает группу из k частиц. Обозначим ξ(t) число частиц, имеющихся к моменту времени t. Очевидно, эволюция величины ξ(t) представляет собой марковский случайный процесс. Процесс такого типа называется ветвящимся процессом. Описанная модель может служить при изучении многих реальных процессов.
Пусть в некоторый исходный момент времени s, скажем s = 0, имеется ровно k частиц. Обозначим ξi (t) число частиц, порожденных i-й частицей, i = 1, ..., k через время t Тогда общее число частиц через время t будет
ξ(t) = ξ1(t) + ... + ξk (t)(10.0)
Здесь случайные величины ξ1(t), ..., ξk(t) независимы между собой и имеют одно и то же распределение вероятностей:
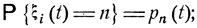
(10.1)
n = 0, 1, ...
Введем производящие функции
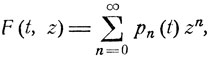
(10.2)
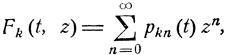
где pkn (t) есть переходные вероятности марковского ветвящегося процесса ξ(t) (pkn (t) есть вероятность того, что k частиц за время t порождают n частиц).
Предположим, что отдельная частица за малый промежуток времени Δt с вероятностью
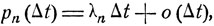
(10.3)
n≠1
превращается в n новых частиц, а с вероятностью
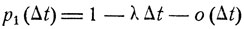
(10.4)
остается неизменной. Пусть, далее,
λ1 = -λ
,
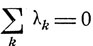
(10.5)
и переходные вероятности pn (t) = p1n (t) удовлетворяют дифференциальным уравнениям Колмогорова (см. (9.10)):
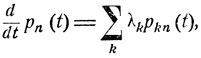
(10.6)
n = 0, 1, ...
При каждом 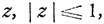 имеем
имеем
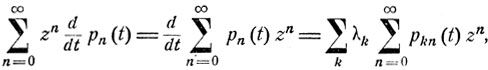
что дает следующее дифференциальное уравнение для производящей функции F(t, z):
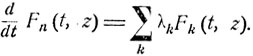
Здесь Fk (t, z) - функции, определенные формулой (10.2),- являются производящими функциями случайной величины ξ(t) для k исходных частиц, k = 0, 1, ... Эта величина ξ(t), согласно равенству (10.0), есть сумма k независимых случайных величин, каждая из которых имеет распределение вероятностей с производящей функцией F(t, z). Поэтому
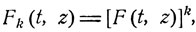
k = 0, 1, ...
(это равенство имеет место и при k = 0), так что дифференциальное уравнение для производящей функции F(t, z) может быть переписано в виде
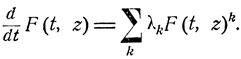
(10.7)
Будем считать, что заданными параметрами ветвящегося процесса ξ(t) являются плотности перехода λk, k = 0, 1, ... Введем функцию
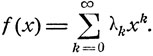
(10.8)
Она является аналитической при 0<x<1, и формула (10.8) дает ее разложение в степенной ряд. Согласно равенству (10.7) производящая функция F(t, z) является решением дифференциального уравнения вида
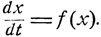
(10.9)
Поскольку F(0, z) = z, производящая функция F(t, z) при каждом z, 0≤z≤1, совпадает с решением x = x(t) этого уравнения, удовлетворяющего начальному условию
x (0) = z.(10.10)
Вместо уравнения (10.9) удобно рассмотреть эквивалентное ему дифференциальное уравнение для обратной к х = x (t) функции t = t(x):
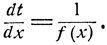
(10.11)
Как решение этого уравнения функция t = t(x) имеет вид
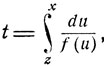
(10.12)
0≤x≤1.
Пример. Пусть плотности перехода суть
λ0 = λ, λ1 = -λ, λk = 0 при k = 2, 3, ...
В этом случае
f(x) = λ(1-x)
и
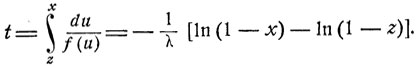
Из этого соотношения легко определяется функция F = F(t, z). Именно,
ln(1-F) = -λt + ln(1-z)
и
F(t, z) = 1-e-λt(1-z).
Вероятности pn (t), определяемые из разложения 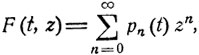 в рассмотренном случае суть
в рассмотренном случае суть
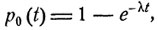
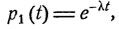
pn (t) = 0,
при n = 2, 3, ...
Пример. Пусть
λ0 = 0, λ1 = -λ,
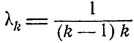
при k = 2, 3, ...
В этом случае
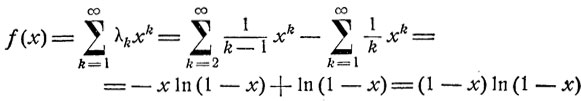
и
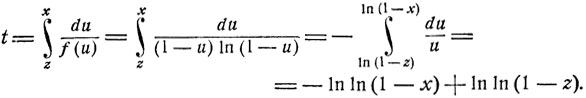
Из этого соотношения легко определяется функция F = F(t, z). Именно,
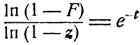
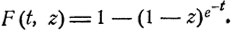
Соответствующие вероятности pn (t) могут быть определены последовательным дифференцированием:
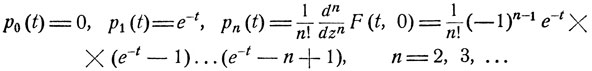
2. Рассмотрим дифференциальное уравнение (10.9), в котором функция f(x) определяется формулой (10.8). Из этой формулы видно, что
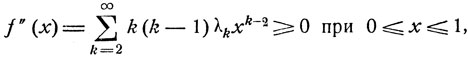
так что функция f (x) является выпуклой, а ее производная f'(x) монотонно возрастает на интервале 0≤x≤1.
Значение х = 1 является корнем уравнения f(x) = 0, так как 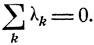 Может быть лишь еще один корень x = α этого уравнения, и в соответствии с этим график функции выглядит так, как указано на рис. 9.
Может быть лишь еще один корень x = α этого уравнения, и в соответствии с этим график функции выглядит так, как указано на рис. 9.
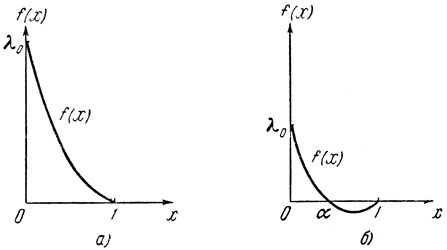
Рис. 9
Остановимся на более сложном случае, когда имеется два корня x = α, 0<α<1, и x = 1, которые определяют две особые интегральные кривые x(t) ≡α и x(t) ≡1 рассматриваемых дифференциальных уравнений. Возьмем интегральную кривую, проходящую через точку t = 0, x = z (0≤z<α):
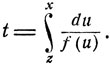
Поскольку производная f' (α) конечна и при x~α функция f(x) имеет вид 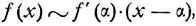 то вдоль интегральной кривой значение
то вдоль интегральной кривой значение 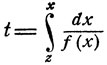 неограниченно возрастает при x→α, причем сама кривая нигде не пересекает другую интегральную кривую x(t) ≡ α. На интервале 0≤х<α Функция f (x) является положительной, и, следовательно, интегральная кривая x = x(t) монотонней возрастает при t→∞, оставаясь ограниченной значением х = α. Как ограниченная монотонная функция, x(t) имеет некоторый предел
неограниченно возрастает при x→α, причем сама кривая нигде не пересекает другую интегральную кривую x(t) ≡ α. На интервале 0≤х<α Функция f (x) является положительной, и, следовательно, интегральная кривая x = x(t) монотонней возрастает при t→∞, оставаясь ограниченной значением х = α. Как ограниченная монотонная функция, x(t) имеет некоторый предел 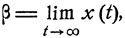 z≤β≤α. Но при x→β функция f(x) имеет своим пределом f(β):
z≤β≤α. Но при x→β функция f(x) имеет своим пределом f(β):
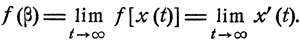
Ясно, что значение f(β) должно быть равно 0, так как в противном случае функция
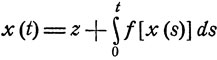
будет неограниченно возрастать при t→∞. Следовательно, β является корнем уравнения f(x) = 0 и совпадает с α: β = α. Таким образом, все интегральные кривые x = x(t), при t = 0 проходящие через точки x = z, 0≤z<α, монотонно возрастают при t→∞ и
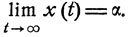
(10.13)
Вполне аналогично поведение интегральных кривых, при t = 0 проходящих через точки x = z, α<z<1. Разница будет лишь в том, что х (t) монотонно убывает, поскольку производная х' (t) = f [x (t)] отрицательна, f(x)≤0 при α<x<1. Общая картина интегральных кривых, отвечающих значениям параметра z в промежутке 0≤z<1, приведена на рис. 10.
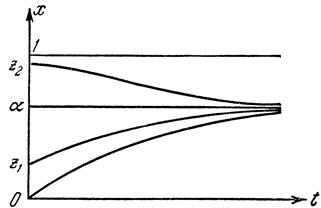
Рис. 10
Случай z = 1 нуждается в особом рассмотрении. Ему всегда отвечает интегральная кривая вида x(t)≡1.
Если для некоторого х0, α<x0<1,
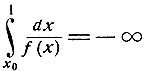
(10.14)
(что всегда так, когда f'(1)<∞), то произвольная интегральная кривая вида
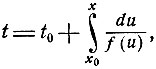
0≤x<1,
проходящая через некоторую точку (t0, x0), при x→1 неограниченно убывает:
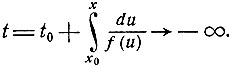
Это говорит о том, что, каково бы ни было t0>0, при некотором x = z, 0≤z<1, имеет место равенство
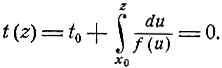
Видно (рис. 11), что все интегральные кривые пересекают ось t = 0 в некоторой точке (0, z), где 0≤z<1, и, следовательно, х(t) ≡ 1 является единственной интегральной кривой, проходящей через точку (0, 1).
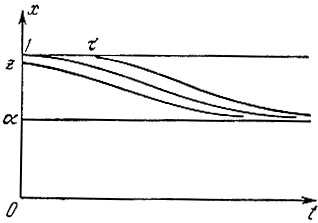
Рис. 11
Если
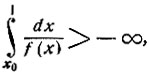
(10ю15)
то при достаточно большом t0>0 интегральная кривая 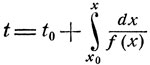 пересекает интегральную кривую x(t) ≡1, касаясь ее в некоторой точке (τ, 1), где
пересекает интегральную кривую x(t) ≡1, касаясь ее в некоторой точке (τ, 1), где
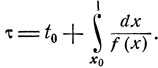
В этом случае через точку (0, 1) проходит целое семейство интегральных кривых xτ(t), каждая из которых отвечает своему значению τ≥. Среди них есть интегральная кривая x0(t), отвечающая значению τ = 0 и обладающая тем свойством, что кривая x0(t) лежит ниже всех остальных интегральных кривых xτ(t):
x0(t)≤xτ(t), 0≤t<∞
Это объясняется тем, что внутри области 0≤x<1, 0<t<∞ решение рассматриваемого дифференциального уравнения единственно и интегральные кривые в этой области не пересекаются друг с другом. Легко видеть также, что эта интегральная кривая x0(t) является предельной для других интегральных кривых x(t, z), лежащих ниже ее и проходящих через соответствующие точки (0, z), где 0≤z<1:
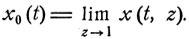
(10.16)
Напомним здесь, что
F(t, z) ≡ x(t, z), t≥0, 0≤z<1.
3. Приведенный выше анализ дифференциального уравнения (10.9) позволяет сделать следующие выводы относительно соответствующего ветвящегося процесса ξ(t).
Вообще говоря, имеется положительная вероятность того, что через некоторое время не останется ни одной частицы. Конечно, этого не может случиться, если λ0 = 0 (т. е. если частицы не могут исчезать, а могут лишь размножаться). Если в исходный момент t = 0 имеется лишь одна частица, то эта вероятность есть p0 (t) = F (t, 0). Если вначале имеется k частиц, то эта вероятность есть pk0(t) = F(t, 0)k = p0(t)k, Как функция от t вероятность p0(t) является решением дифференциального уравнения (10.9), отвечающим параметру z = 0:
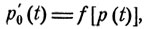
p0 = 0.
Как было показано, это решение при 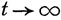 асимптотически приближается к некоторому значению p0 = α, являющемуся наименьшим корнем уравнения f(x) = 0 (см. соотношение (10.13)), т. е.
асимптотически приближается к некоторому значению p0 = α, являющемуся наименьшим корнем уравнения f(x) = 0 (см. соотношение (10.13)), т. е.
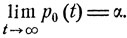
(10.17)
Таким образом, р0 = α есть вероятность вырождения ветвящегося процесса ξ(t) (вероятность того, что к некоторому моменту времени не остается ни одной частицы). Если функция f(х) является положительной на интервале 0≤x<1 то вероятность вырождения ветвящегося процесса ξ(t) равна 1.
Рассмотрим так называемое явление взрыва, когда образуется бесконечно много частиц. Вероятность того, что взрыв произойдет до момента t, есть
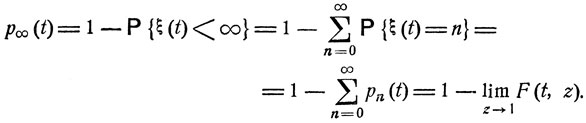
В случае, когда x(t) ≡ 1 является единственной интегральной кривой дифференциального уравнения (10.9), проходящей через точку (0, 1), этот предел lim F(t, z), очевидно, равен 1. Следовательно, при условии (10.14) вероятность p∞(t) = 0 при любом t, так что возможность взрыва исключена. При условии же (10.15) функции x(t, z) при z→1 монотонно сходятся к описанной выше функции х0(t) (см. соотношение (10.16)), так что

(10.18)
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'