§ 9. Марковские процессы с конечным или счетным числом состояний. Дифференциальные уравнения Колмогорова. Финальные распределения вероятностей

1. Так же как и при рассмотрении марковских цепей (см. § 7), будем условно говорить о некоторой физической системе, с течением времени t меняющей свое фазовое состояние. Так же как и раньше, будем считать, что имеется лишь конечное или счетное число различных фазовых состояний ε₁, ε₂, ... Обозначим ξ(t) состояние системы в момент времени t. Процесс эволюции рассматриваемой системы описывается функцией ξ(t).

Будем предполагать, что течение этого процесса ξ(t) зависит от вмешательства случая, причем соблюдается следующая закономерность: если в какой-либо момент времени s система находится в состоянии ε_i, то, независимо от своего поведения до этого момента s, она через время t с вероятностью p_ij (t) переходит в состояние ε_j.

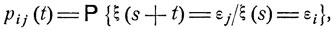
(9.0)

i, j = 1, 2, ...

Описанная модель называется однородным марковским случайным процессом, а вероятности p_ij называются переходными вероятностями этого процесса. Кроме них, еще задается начальное распределение вероятностей

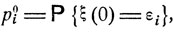
(9.1)

i = 1, 2, ...

Обозначим p_j (t) вероятность того, что через время t система будет находиться в состоянии ε_j.

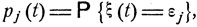
(9.2)

j = 1, 2, ...

Легко установить (ср. (7.5), (7.6)), что

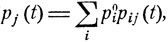
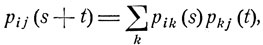
(9.3)

i, j = 1, 2, ...,

при любых s и t, где

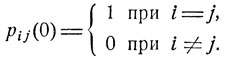
(9.4)

Предположим, что в некоторый момент времени t = t₀ марковский процесс ξ(t) находится в определенном состоянии ε. Через некоторое случайное время х процесс переходит в некоторое другое состояние. Какова вероятность того, что изменение фазового состояния произойдет не раньше, чем через время t?

Эта вероятность 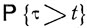зависит, конечно, от t Рассматривая ее как функцию от t, положим

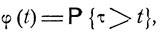
t≥0.

При условии, что τ>s, в момент t₀+s процесс будет находиться в том же состоянии ε, и дальнейшее его поведение подчиняется тем же закономерностям, что и при s = 0, в частности, при условии τ>s вероятность события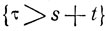

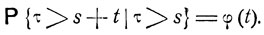
Используя формулу полной вероятности, получаем, что

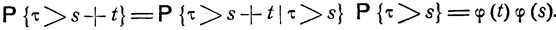
Это дает следующее соотношение для функции φ:

при любых s и t, откуда

Видно, что функция ln φ(t) является линейной:

где х - некоторая неотрицательная постоянная. Таким образом, искомая вероятность есть

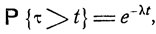
(9.5)

t≥0.

Параметр λ называется плотностью перехода из соответствующего состояния ε. При λ = 0 процесс навсегда остается в состоянии ε. При λ>0 вероятность того, что состояние процесса претерпевает изменение за малый промежуток времени Δt, есть

где o(Δt) означает величину высшего порядка малости по сравнению с Δt.

Распределение вероятностей случайной величины τ - времени до момента перехода в новое состояние - таково, что

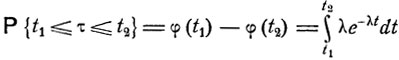
(9.7)

при любых t₁, t₂≥0. Оно называется показательным или экспоненциальным распределением. Видно, что плотность такого распределения вероятностей имеет вид

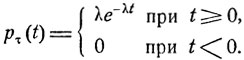
Среднее значение Мτ случайной величины τ - среднее время ожидания перемены состояния - определяется формулой

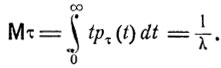
Процесс радиоактивного распада. Описанная ранее вероятностная модель радиоактивного распада - превращения радия Ra в радон Rn (см. п. 1 § 6) - такова, что переход Ra→Rn представляет собой однородный марковский процесс с двумя состояниями для каждого атома (Ra или Rn) и единственно возможным переходом Ra→Rn. Вероятность того, что атом Ra за время t перейдет в атом Rn, ранее была обозначена p(t). Было показано, что если в исходный момент времени t = 0 количество атомов Ra равно n₀, то число ξ(t) испускаемых за время t α-частиц имеет распределение Пуассона с параметром a = n₀p (t):

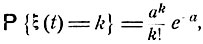
Здесь р (t) - вероятность того, что состояние Ra изменится за время t,- согласно общей формуле (9.5) имеет вид

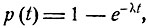
t≥0,

где λ - соответствующая плотность перехода Ra→Rn для отдельного атома, т. е. такая постоянная, что вероятность перехода Ra→Rn за малый промежуток времени Δt есть λΔt + o(Δt).

Рассмотрим количество радия через время t Если число α-частиц равно ξ(t), то число оставшихся атомов Ra равно n₀ - ξ(t). Среднее количество радия через время t есть

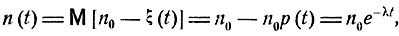
t≥0.

Экспоненциальный характер функции n (t) говорит, в частности, о том, что время Т, за которое в среднем распадается половина исходного количества радия:

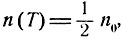
есть некоторая абсолютная постоянная. Это - так называемая постоянная полураспада. Видно, что она связана с плотностью перехода Ra→Rn равенством

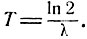
2. Рассмотрим марковский процесс ξ (t) с переходными вероятностями p_ij (t), i, j = 1, 2, ...

Будем считать, что переходные вероятности p_ij (t) удовлетворяют следующим условиям:

Здесь λ_i - плотность перехода из состояния ε_i, λ_ij - так называемые плотности перехода из ε_i в соответствующее состояние ε_j. Положим

Теорема. Для марковского процесса с конечным числом состояний переходные вероятности p_ij (t) удовлетворяют дифференциальным уравнениям

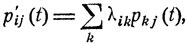
(9.10)

i,j = 1, 2, ...,

и

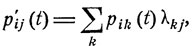
(9.11)

i,j = 1, 2, ...,

с начальными условиями (9.4).

Уравнения (9.11) образуют так называемую прямую систему, а уравнения (9.10) - обратную систему дифференциальных уравнений Колмогорова.

Доказательство. Согласно общей формуле (9.3)

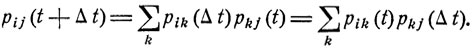
Используя асимптотические выражения (9.9), получаем, что

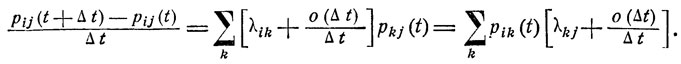
Правые части этих равенств имеют вполне определенный предел при Δt→0:

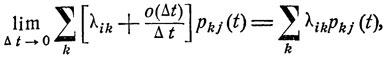
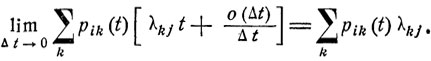
Следовательно, существует и предел

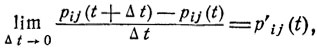
причем должны быть выполнены равенства (9.10) и (9.11).

Теорема доказана.

Следует отметить, что указанные дифференциальные уравнения для переходных вероятностей р_ij (t) имеют место не только в случае конечного числа состояний, но при некоторых дополнительных ограничениях и в случае счетного числа состояний ε₁, ε₂, ... Использованный выше прием для вывода этих дифференциальных уравнений остается в силе, если в асимптотических выражениях (9.9) остаточные члены о(Δt) таковы, что

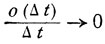
при Δt→0

равномерно по всем i, j. Уравнение (9.10) будет иметь место, если сходится ряд 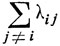и

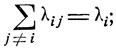
(9.12)

уравнение (9.11) будет иметь место, если при фиксированном j плотности перехода λ_ij равномерно ограничены:

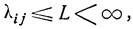
(9.13)

i = 1, 2, ...

Пуассоновский процесс. В п. 1 § 7 была рассмотрена задача о потоке требований, поступающих на некоторую систему обслуживания. Проведенный там предварительный анализ показывает, что поток требований ξ (t) ξ (t) означает число требований" поступивших за время t) является марковским процессом, состояния которого могут быть описаны целыми числами 0, 1, ...

Из состояния i можно непосредственно перейти лишь в следующее состояние j = i+1, i = 1, 2, ..., и плотности перехода λ_ij таковы, что

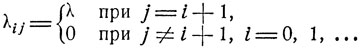
Для переходных вероятностей p_ij (t) имеет место система дифференциальных уравнений (9.11). Очевидно, p_ij (t) = p_{0, j-i}) (t). Положим

Указанные дифференциальные уравнения для функций p_j (t) выглядят следующим образом:

Если перейти к новым функциям 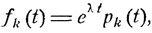то получим, что

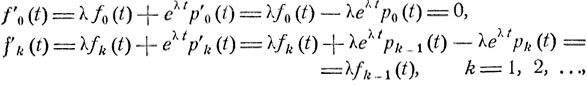
где

Система дифференциальных уравнений вида

с указанными начальными условиями имеет, очевидно, следующее решение:

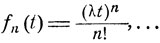
Возвращаясь к исходным функциям 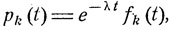получаем, что

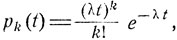
Система с экспоненциальным временем обслуживания. Предположим, что на некоторую систему обслуживания поступает пуассоновский поток требований с параметром λ₀, т. е. различные требования поступают независимо одно от другого и вероятность поступления отдельного требования в малом промежутке времени Δt есть λ₀Δt + o(Δt). Пусть на обслуживание каждого отдельного требования затрачивается случайное время τ, распределенное по экспоненциальному закону с параметром λ₁, т. е.

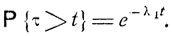
Рассмотрим два состояния системы обслуживания: ε₀ - система свободна, ε₁ -"система замята. Будем считать, что если система занята, то поступающие в это время требования получают отказ и уходят из сферы обслуживания.

Предположим, что система в некоторый момент времени t₀ находится в состоянии ε₀. В силу независимости поступления требований ее дальнейшее поведение не зависит от предшествующих обстоятельств и, в частности, за время Δt она с вероятностью λ₀Δt + o(Δt) перейдет в состояние ε₁. Предположим, что в момент t₁ система находится в состоянии ε₁.

Если обозначить τ₁ случайный момент перехода из ε₁ в ε₀ (момент окончания обслуживания), то, согласно экспоненциальному закону распределения времени обслуживания - величины τ = τ₁ - t₁ имеет место следующее равенство:

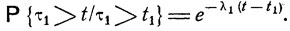
Видно, что переход в ε₀ и дальнейшее поведение системы не зависят от ее поведения до момента t₁. В частности, в последующем за t₁ промежутке времени Δt система с вероятностью λ₁ Δt + o (Δt) переходит в состояние ε₀. Таким образом, эволюция системы описывается марковским процессом с двумя состояниями ε₀, ε₁ и соответствующими плотностями перехода λ₀, λ₁.

Пусть p_ij (t) - соответствующие переходные вероятности. В рассматриваемом случае p₀₁ (t) = 1 - р₀₀ (t), p₁₀ (t) = 1 - р₁₁ (t) и дифференциальные уравнения (9.11) имеют вид:

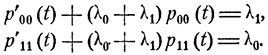
Решая их, получаем, что

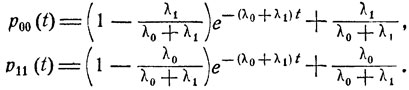
3. Рассмотрим марковский процесс с конечным числом состояний ε₁, ..., ε_m, каждое из которых достижимо из любого другого состояния.

Теорема. Вероятности p_j (t), с которыми через время t система будет находиться в соответствующих состояниях ε_j (j = 1, ..., m), при t→∞ со имеют предельные значения

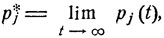
(9.14)

j = 1, ..., m.

Указанные финальные вероятности не зависят от начального распределения и, более того,

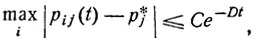
(9.15)

где С и D - некоторые положительные постоянные.

Доказательство совершенно аналогично тому, что было дано в случае марковских цепей (см. формулу (8.14)). В случае непрерывного времени t предполагавшееся ранее условие (8.12) выполняется автоматически; именно

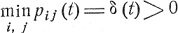
(9.16)

при любом t>0,

Чтобы установить это, рассмотрим сначала вероятность p_ii (t), которая как функция от t является непрерывной и р_ii (0) = 1, так что при достаточно малых t эта вероятность является положительной. Но из соотношения (9.3) видно, что при любых s и t

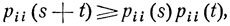
так что на самом деле вероятность p_ii (t) положительна при всех t. Рассмотрим теперь состояние ε_j, достижимое из состояния ε_i, т. е. такое, что p_ij (s)>0 при некотором s. Покажем, что тогда вероятность p_ij (t) является положительной для любого t>0. Имеем:

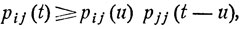
u≤t.

Как показано выше, p_jj (t - u) всегда положительна, так что достаточно показать, что p_ij (u)>0 при некотором u≤t. По предположению p_ij (s)>0. Рассмотрим цепь Маркова с переходными вероятностями 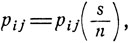где натуральное число n удовлетворяет условию 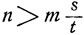(m - число состояний). Поскольку 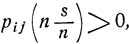состояние ε_j достижимо из ε_i. Легко видеть, что оно достижимо не только за n шагов, но и за некоторое число шагов n₀, не превосходящее число m всех имеющихся состояний, т. 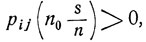е. где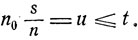

Доказательство закончено.

Финальные вероятности p_i^*, i = 1, 2, ..., задают стационарное распределение вероятностей: если в качестве начального распределения взять 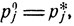i = 1, 2, ..., то соответствующие вероятности p_j (t), с которыми система через время t будет находиться в соответствующих состояниях ε_j, остаются неизменными с течением времени t:

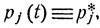
если 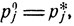j = 1, 2, ... (9.17)

Это вытекает из соотношения

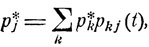
(9.18)

j = 1, 2, ...,

которое получается из общего равенства (9.3) при переходе к пределу, когда s→∞. В самом деле, правая часть равенства (9.18), согласно формуле (9.3), и есть соответствующая вероятность p_j (t), а в левой части стоит финальная вероятность р^*_j.

Отметим, что если взять производные при t = 0 от обеих частей равенства (9.18), то получим следующее соотношение для финальных (стационарных) вероятностей р^*_j:

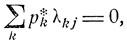
(9.19)

j = 1, 2, ...,

где λ_kj - плотности перехода рассматриваемого марковского процесса.

Система обслуживания. Формулы Эрланга. Рассмотрим систему, которая может обслуживать одновременно m требований. Будем считать, что имеется m линий и очередное требование поступает на одну из линий, если хотя бы одна из них свободна; в противном случае поступающее требование получает отказ и уходит из сферы обслуживания. Предположим, что поток требований является пуассоновским с параметром λ₀ и время обслуживания каждого требования (на каждой из m линий) распределено по показательному закону с параметром λ.

Рассмотрим состояния ε₀, ε₁, ..., ε_m, где ε_k означает, что занято ровно k линий. В частности, ε₀ означает, что система свободна, а ε_m - что система полностью занята. Переход системы из состояния в состояние с течением времени t представляет собой марковский процесс, для которого плотности перехода имеют вид

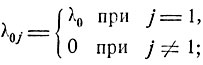
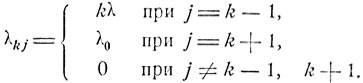
Действительно, переход из ε_k в ε_j осуществляется при поступлении очередного требования, что происходит за время Δt с вероятностью λ₀Δt + o(Δt). Вероятность того, что ни одна из k занятых линий не освободится за время Δt, есть [1-λΔt-o(Δt)]^k (поскольку линии обслуживаются независимо одна от другой), и вероятность освобождения одной из линий, т. е. перехода из состояния ε_k в ε_j, j = k-1, есть 1-[1-λΔt - o (Δt)]^k = kλΔt + o(Δt). Вероятность других изменений в системе за промежуток времени Δt есть o (Δt).

Как непосредственно видно из выражений для переходных вероятностей р_ij (t), полученных ранее в случае m = 1 (см. стр. 96), при t→∞ вероятности p_ij (t) экспоненциально быстро стремятся к своим финальным значениям. То же, согласно общей формуле (9.15), наблюдается и в случае m линий. Финальные вероятности р_ij (t) могут быть найдены из соотношений (9.19), которые дают следующую систему уравнений для определения неизвестных р^*_k:

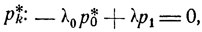
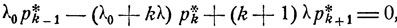
1≤k<m,

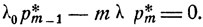
Из этих уравнений получаем, что

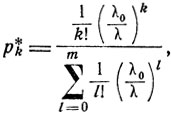
k = 0, 1, ..., m.

Найденные выражения для финальных вероятностей называются формулами Эрланга.