
§ 8. Цепи Маркова. Возвратные и невозвратные состояния. Финальные распределения вероятностей. Стационарность
1. Условно будем говорить о некоторой физической системе, шаг за шагом меняющей свое фазовое состояние. Будем считать, что имеется лишь конечное или счетное число различных фазовых состояний ε1, ε2, ... Обозначим ξ(n) состояние системы через n шагов. Будем предполагать, что цепочка последовательных переходов
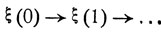
зависит от вмешательства случая, причем соблюдается следующая закономерность: если на каком-либо шаге n система находится в состоянии εi, то, независимо от предшествующих обстоятельств, она на следующем шаге с вероятностью pij переходит в состояние εj.
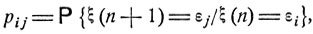
(8.0)
i,j = 1, 2, ...
Описанная выше модель называется однородной цепью Маркова, а вероятности pij называются переходными вероятностями этой цепи. Кроме них, еще задается начальное распределение вероятностей
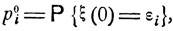
(8.1)
i = 1, 2, ...
Какова вероятность того, что система через n шагов будет находиться в состоянии εj?
Обозначим эту вероятность pj (n):
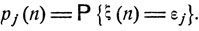
(8.2)
Через n-1 шагов система обязательно будет находиться в одном из состояний εk, k = 1, 2, ..., причем в εk она будет с вероятностью, обозначенной pk (n-1). При условии, что через n-1 шагов система будет находиться в состоянии εk, вероятность оказаться через n шагов в состоянии εj равна вероятности pkj перехода из εk в εj. Используя формулу полной вероятности, получаем, что
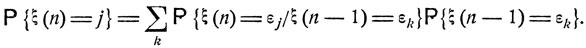
(8.3)
Это дает следующие рекуррентные соотношения для вероятностей рj (n), j = 1, 2, ...:
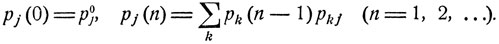
(8.4)
Если в начальный момент система находится в определенном состоянии εi, то начальное распределение вероятностей таково, что рi0 = 1, р0k = 0 для k≠i, а вероятность pj (n) совпадает с вероятностью pij (n) того, что система из состояния εi за n шагов перейдет в состояние εj.
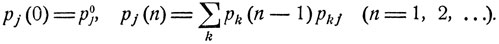
(8.5)
i,j = 1, 2, ...
При начальном распределении вида рi0 = 1, рk0 = 0 для k≠i формула (8.4) дает следующие соотношения между переходными вероятностями рij (n); i, j = 1, 2, ...:
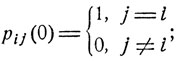
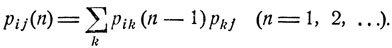
(8.6)
Удобно ввести матрицу 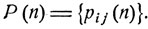 Согласно формуле (8.6)
Согласно формуле (8.6)
P(0) = I, P(1) = P, P(2) = P(1)P = P2, ...,
где I - единичная матрица, 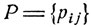 - матрица переходных вероятностей. Видно, что имеет место следующее равенство:
- матрица переходных вероятностей. Видно, что имеет место следующее равенство:
P (n) = Pn, (n = 1, 2, ...).
Рассмотрим несколько примеров.
Задача о стопке книг. На письменном столе лежит стопка из m книг. Если обозначить каждую книгу соответствующим номером, то порядок их расположения сверху вниз можно описать перестановкой из m чисел (i1, i2, ..., im), где i1 - номер книги, лежащей сверху, i2 - номер следующей книги, ..., im - номер последней книги, лежащей в самом низу. Предположим, что каждая книга берется с определенной вероятностью, скажем, книга с номером k берется с вероятностью pk (k = 1, ..., m), причем при возвращении она кладется сверху.
Возьмем произвольное состояние (i1, i2, ..., im). На следующем шаге оно либо остается неизменным, что происходит с вероятностью pi1 при выборе лежащей сверху книги с номером i1, либо меняется на одно из m-1 состояний вида (ik, i1, ...), что происходит с вероятностью рik при выборе книги с номером ik.
Перед нами цепь Маркова с состояниями, каждое из которых описывается соответствующей перестановкой (i1, i2, ..., im), и указанными переходными вероятностями.
Остановимся на случае m = 2. Тогда имеется лишь два состояния: ε1 = (1, 2) и ε2 = (2, 1). Переходные Вероятности имеют вид:
p11 = p21 = p1, p12 = p22 = p2
и матрица переходных вероятностей есть
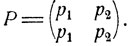
Вероятности перехода за два шага суть
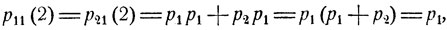
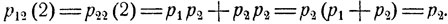
Видно, что Р2 = Р и вообще Рn = Р. При любом начальном распределении вероятностей имеем (n = 1, 2, ...)
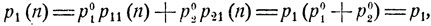
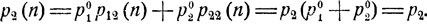
Задача о наилучшем выборе (см. п. 1 § 3). Положим ξ0(0) = 1 и обозначим: ξ(1)- порядковый номер первого предмета, оказавшегося наилучшим среди всех осмотренных ранее; ξ(2) - порядковый номер следующего наилучшего среди всех осмотренных до него предметов и т. д. Цепочка 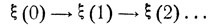 обрывается на некотором v-м шаге, если предмет с порядковым номером ξ(v) оказывается абсолютно наилучшим, так что и среди не осмотренных еще предметов нет лучшего. Число v является случайным, поскольку случайным является сам порядок осмотра. Введем состояния ε1, ε2, ..., εm, εm+1, охарактеризовав их следующим образом: ε1 при i = 1, ..., m означает, что предмет с порядковым номером i (т. е. i-й по счету осмотренный предмет) является наилучшим среди всех ранее осмотренных; εm+1 означает, что уже осмотрен абсолютно наилучший предмет. Если положить ξ(n) = εm+1 при всех n>v, то последовательность
обрывается на некотором v-м шаге, если предмет с порядковым номером ξ(v) оказывается абсолютно наилучшим, так что и среди не осмотренных еще предметов нет лучшего. Число v является случайным, поскольку случайным является сам порядок осмотра. Введем состояния ε1, ε2, ..., εm, εm+1, охарактеризовав их следующим образом: ε1 при i = 1, ..., m означает, что предмет с порядковым номером i (т. е. i-й по счету осмотренный предмет) является наилучшим среди всех ранее осмотренных; εm+1 означает, что уже осмотрен абсолютно наилучший предмет. Если положить ξ(n) = εm+1 при всех n>v, то последовательность 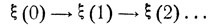 образует цепь Маркова.
образует цепь Маркова.
Найдем соответствующие переходные вероятности рij. Очевидно, рij = 0 при i≥j, j≤m, a pm+1, m+1 = 1. Подсчитаем вероятности рij при i<j≤m. Обозначим εj событие,
состоящее в том, что при случайном порядке осмотра j предметов наилучшим среди них является последний j-й предмет. Очевидно, переходные вероятности рij согласно общей формуле (8.0) совпадают с условными вероятностями
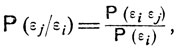
i<j≤m.
Очевидно, вероятность события εj совпадает с вероятностью того, что среди всех перестановок из j предметов будет выбрана та, при которой на последнем месте стоит наилучший предмет. Всего различных перестановок имеется j!, а тех, при которых на последнем месте оказывается один и тот же фиксированный элемент, имеется (j-1)! Следовательно,
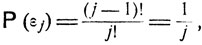
j = 1, ..., m.
Вероятность события εiεj совпадает с вероятностью того, что на последнем месте стоит наилучший предмет, а на i-м месте стоит также вполне определенный предмет - второй по качеству среди всех j предметов. Всего имеется (j-2)! таких перестановок и, следовательно,
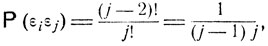
i<j≤m.
Таким образом, переходные вероятности pij суть
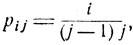
i<j≤m.
Переходные вероятности рi,m фактически были подсчитаны ранее (см. п. 1 § 3):
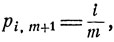
i = 1, ..., m.
Случайные блуждания. Рассмотрим случайное блуждание, связанное с неограниченными испытаниями Бернулли, когда частица блуждает по целочисленным точкам действительной прямой таким образом, что, находясь в точке i, она с вероятностью р переходит на следующем шаге в соседнюю точку i+1, а с вероятностью q = 1 - p - в соседнюю точку i-1. Если обозначить ξ(n) положение частицы после n шагов, то последовательность 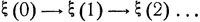 будет цепью Маркова с переходными вероятностями вида
будет цепью Маркова с переходными вероятностями вида
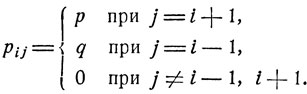
Рассмотрим случайное блуждание другого типа. Частица блуждает лишь по целым неотрицательным точкам, причем из точки i она с вероятностью pi переходит на следующем шаге в соседнюю точку i+1, а с вероятностью qi = 1-pi возвращается в нулевое положение. Соответствующие переходные вероятности суть
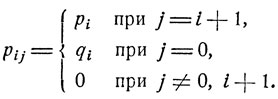
2. Рассмотрим цепь Маркова с состояниями ε1, ε2, ... и переходными вероятностями pij, i,j = 1, 2,... Цусть в начальный момент система находится в состоянии εi. Временно положим un = pii (n) и обозначим vn вероятность того, что через n шагов система впервые вернется в исходное состояние εi. Имеет место следующее равенство:
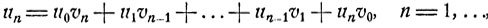
(8.8)
где дополнительно введены u0 = 1 и v0 = 0.
Оно является следствием общей формулы полной вероятности. Именно, если ввести события Bk - "система через k шагов впервые возвращается в исходное состояние εi", k = 1, ..., n, и событие Bn+1 - "система ни разу не побывает в состоянии εi в течение первых n шагов", то B1, ..., Вn+1 будет полной системой событий, и вероятность события А - "система через n шагов будет находиться в исходном состоянии εi" - по формуле полной вероятности есть
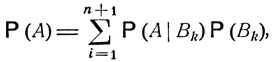
где
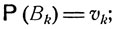
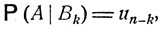
k = 1, ..., n;
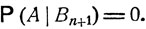
Если обратиться к производящим функциям
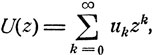
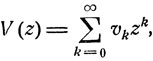
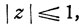
то отношение (8.8), справедливое при всех n = 1, 2,... , можно записать в виде
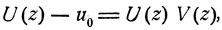
u0 = 1,
откуда
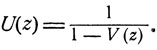
Значение
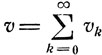
есть вероятность того, что система рано или поздно попадет в исходное состояние εi, иначе v есть вероятность возвращения в εi. Состояние εi называется возвратным, если вероятность возвращения в него равна 1, и невозвратным, если вероятность эта меньше 1.
Теорема. Состояние εi является возвратным тогда и только тогда, когда
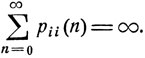
(8.11)
Доказательство. Возвратность состояния εi означает, что
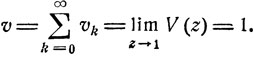
Это предельное соотношение равносильно тому, что
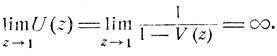
Но, как легко видеть,
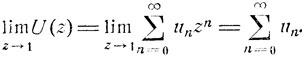
Таким образом, возвратность состояния εi равносильна тому, что ряд 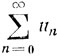 расходится. Для завершения доказательства остается лишь напомнить, что un = pii (n).
расходится. Для завершения доказательства остается лишь напомнить, что un = pii (n).
Теорема. Если исходное состояние εi является возвратным, то система с вероятностью 1 за бесконечное число шагов бесконечно много раз возвратится в εi. Если это состояние является невозвратным, то за бесконечное число шагов система с вероятностью 1 лишь конечное число раз побывает в состоянии εi, другими словами, после некоторого конечного числа шагов она никогда больше не возвращается в εi.
Доказательство. Обозначим v1 - число шагов до первого возвращения в состояние εi, v2 - число шагов до второго возвращения и т. д. Если за бесконечное число шагов происходит меньше k возвращений, то полагаем vk = ∞.
Событие 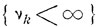 означает, что произошло по меньшей мере k возвращений. Вероятность возвращения есть
означает, что произошло по меньшей мере k возвращений. Вероятность возвращения есть
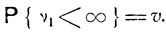
При условии осуществления события  система через некоторое конечное число шагов v1 возвращается в исходное состояние εi, после чего ее дальнейшее поведение подчиняется тем же закономерностям, как если бы она только начинала свое движение. Таким образом, вероятность события
система через некоторое конечное число шагов v1 возвращается в исходное состояние εi, после чего ее дальнейшее поведение подчиняется тем же закономерностям, как если бы она только начинала свое движение. Таким образом, вероятность события 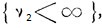 при условии, что
при условии, что  , будет равна υ:
, будет равна υ:
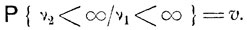
Очевидно, если v1 = ∞, то также и v2 = ∞. Поэтому
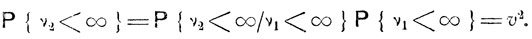
Совершенно аналогично при любом k
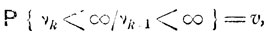
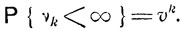
Невозвратность состояния εi означает, что υ<1. В этом случае
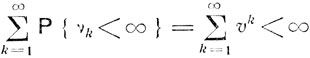
и, согласно первой лемме Бореля - Кантелли (см. п. 1 § 4), с вероятностью 1 может произойти лишь конечное число событий вида 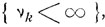 т. е. с вероятностью 1 за бесконечное число шагов система лишь конечное число раз побывает в состоянии εi.
т. е. с вероятностью 1 за бесконечное число шагов система лишь конечное число раз побывает в состоянии εi.
Возвратность состояния εi означает, что v = 1. В этом случае при любом k
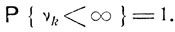
Обозначим х число возвращений за бесконечное число шагов. Очевидно, событие 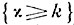 тождественно с событием
тождественно с событием 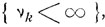 , так что, если P
, так что, если P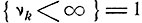 при всех k, то с вероятностью 1 величина х превосходит любое наперед заданное число k. Это значит, что
при всех k, то с вероятностью 1 величина х превосходит любое наперед заданное число k. Это значит, что
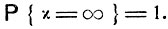
Теорема доказана.
Говорят, что состояние εj достижимо из εi, если за некоторое число шагов система с положительной вероятностью переходит из εi в εj, т. е. pij (М)>0 при некотором М.
Пусть εi - возвратное состояние и εj достижимо из εi. Тогда εi в свою очередь достижимо из εj, так как в противном случае, выходя из εi, система за М шагов с положительной вероятностью pij (М) = α> 0 попадает в состояние εj, после чего уже не может вернуться в εi; таким образом, вероятность возвращения в εi будет не больше, чем 1-α, а это противоречит возвратности εi. Итак, если εj достижимо из возвратного состояния εi, то в свою очередь εi достижимо из εj, т. е. рij (N) = β> 0 при некотором N. Как следует из формулы (8.7), при любом n
Р (n + М + N) = P (М) Р (n) Р (N) = Р (N) Р(n) Р (M),
откуда
pii (n + M + N) ≥ pij (M) pjj (n) pji (N) = αβ pjj (n).
pjj (n + M + N) ≥ pji (M) pii (n) pij (N) = αβ piij (n).
Эти неравенства показывают, что ряды
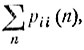
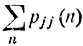
сходятся или расходятся одновременно. Согласно условию (8.11), для возвратного состояния εi ряд 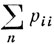 расходится.
расходится.
Поэтому также и
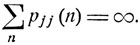
Следовательно, состояние εj является возвратным. Мы пришли к следующему результату.
Теорема. Если состояние εj достижимо из возвратного состояния εi, то εj также является возвратным, причем εi в свою очередь достижимо из εj.
Следствие. Если цепь Маркова имеет лишь конечное число состояний, причем каждое из них достижимо из любого другого состояния, то все они являются возвратными.
Действительно, если имеется лишь конечное число состояний, то за бесконечное число шагов хотя бы в одном из них система обязательно побывает бесконечное число раз. Следовательно, хотя бы одно состояние является возвратным, а поскольку по условию из него можно с положительной вероятностью перейти в любое другое состояние, все они будут возвратными.
Рассмотрим примеры, описанные в предыдущем пункте.
Задача о стопке книг. Очевидно, если каждая книга выбирается с положительной вероятностью, т. е. pi>0 при всех i = 1, ..., m, то любое состояние достижимо из каждого другого состояния. Всего имеется m! различных состояний (i1, ...., im) и все они будут возвратными. Если pi = 0 при некотором i, то все состояния вида (i1, ..., im), где i1 = i (книга с номером i лежит на самом верху), являются невозвратными, так как после первого же шага выбирается некоторая книга с номером j, отличным от i, и книга с номером i, никогда не вынимаемая из стопки, опускается ниже.
Задача о наилучшем выборе. Очевидно, через некоторое число шагов, не больше m (m - число всех имеющихся предметов), система попадает в состояние εm+1, в котором остается навсегда. Таким образом, все состояния, кроме εm+1, являются невозвратными.
Случайные блуждания. Рассмотрим случайное блуждание, при котором частица из каждой целочисленной точки i на следующем шаге с вероятностью р переходит в соседнюю точку j = i+1, а с вероятностью q - в точку j = i-1. Ясно, что каждое состояние достижимо из любого другого состояния и (см. формулу (6.0))
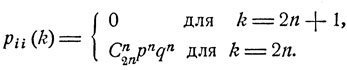
Используя формулу Стерлинга, при 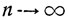 получаем
получаем
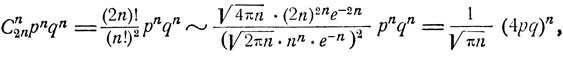
где
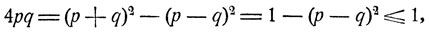
причем знак равенства имеет место лишь при 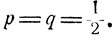
Таким образом, при 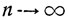
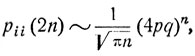
откуда следует, что ряды
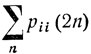
и
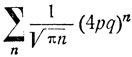
сходятся или расходятся одновременно. При р≠q, когда 4pq<1, ряд 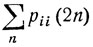 сходится, и следовательно, каждое состояние является невозвратным. Интуитивно ясно, что, например, при p>q блуждающая частица постепенно будет уходить все дальше и дальше в положительном направлении, рано или поздно навсегда покидая любое фиксированное состояние i. При неограниченно продолжающемся симметричном случайном блуждании, когда
сходится, и следовательно, каждое состояние является невозвратным. Интуитивно ясно, что, например, при p>q блуждающая частица постепенно будет уходить все дальше и дальше в положительном направлении, рано или поздно навсегда покидая любое фиксированное состояние i. При неограниченно продолжающемся симметричном случайном блуждании, когда 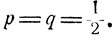 , частица бесконечное число раз возвращается в каждое из состояний.
, частица бесконечное число раз возвращается в каждое из состояний.
Рассмотрим теперь случайное блуждание, при котором частица из неотрицательной целой точки i на следующем шаге с вероятностью pi смещается в соседнюю точку j = i+1, а с вероятностью qi = 1-pi переходит в нулевую точку j = 0. Очевидно, если все вероятности pi таковы, что 0<pi<1, то все состояния являются достижимыми одно из другого. Все они будут возвратными или невозвратными.
Предположим, что система находится в состоянии i = 0. Вероятность того, что за последующие n шагов она ни разу не вернется в исходное положение i = 0, равна произведению p0p1...pn-1 - вероятности того, что система последовательно пробегает цепочку состояний 0→1→ ... →n. Легко видеть, что вероятность за бесконечное число шагов ни разу не вернуться в исходное состояние i = 0 равна бесконечному произведению
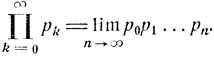
Если это бесконечное произведение сходится к нулю: 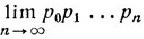 = 0, то состояние i = 0 (а вместе с ним и все остальные) является возвратным. В противном случае вероятность возвращения есть
= 0, то состояние i = 0 (а вместе с ним и все остальные) является возвратным. В противном случае вероятность возвращения есть
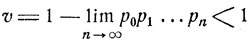
и состояние i = 0 (а вместе с ними все остальные) является невозвратным.
К этому результату можно прийти и другим путем, непосредственно рассматривая вероятности vk впервые вернуться в исходное состояние 0 ровно через k шагов. Очевидно, частица впервые возвращается в состояние 0 на k-м шаге, если она на первых k-1 шагах последовательно переходит из состояния i-1 в i (с вероятностями pi-1, i = 1, ..., k-1), и потому
v1 = 1-р0, vk = p0...pk-2(1-pk-1); k = 2,3,...
Вероятность возвращения в исходное состояние 0 по определению равна сумме 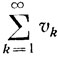 и есть
и есть
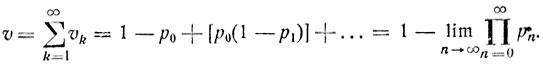
3. Рассмотрим цепь Маркова с конечным числом состояний ε1, ..., εm, каждое из которых достижимо из любого другого состояния. Более того, предположим, что существует такое N, что за N шагов система с положительной вероятностью может перейти из каждого состояния εi в любое другое состояние εj, т. е.
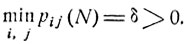
(8.12)
Теорема. Вероятности рj (n), с которыми через n шагов система будет находиться в соответствующих состояниях εj, j = 1, ..., m, при n→∞ имеют предельные значения
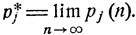
(8.13)
Указанные финальные вероятности p*j j = 1, ..., m, не зависят от начального распределения и, более того,
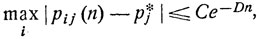
(8.14)
где С и D - некоторые положительные постоянные.
Доказательство. Положим
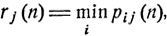
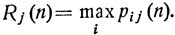
Имеем
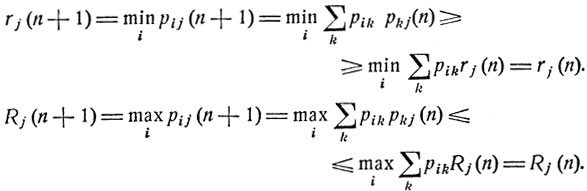
Таким образом, получаем следующую цепочку неравенств:

Для любых состояний εα и εβ
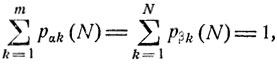
где 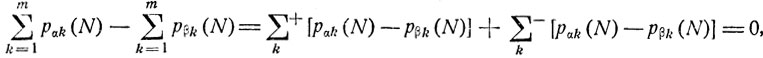 означает суммирование по всем тем k, при которых разность рαk(N) - рβk (N) является положительной, а
означает суммирование по всем тем k, при которых разность рαk(N) - рβk (N) является положительной, а 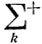 суммирование по всем тем k, при которых разность рαk(N) - рβk (N) является отрицательной. Очевидно, в силу условия (8.12)
суммирование по всем тем k, при которых разность рαk(N) - рβk (N) является отрицательной. Очевидно, в силу условия (8.12)
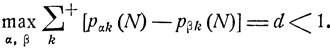
Используя полученные соотношения, оценим разность Rj (n) - rj (n). Имеем
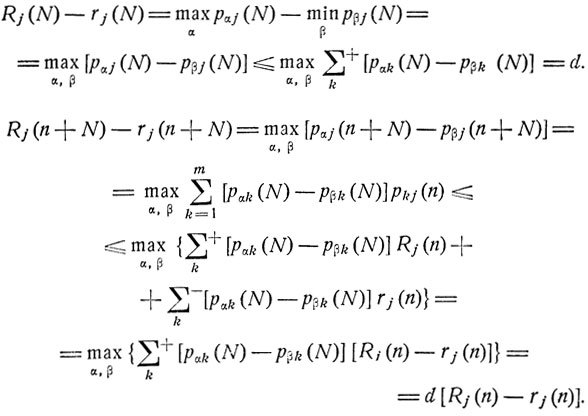
Отсюда вытекает, что
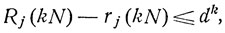
k = 1, 2, ...
Последовательность rj (n), n = 1, 2, ..., монотонно возрастает, а последовательность Rj (n), n = 1, 2, ..., монотонно убывает, причем rj (n) ≤ Rj (n). Полученная выше оценка разности Rj (n) - rj (n) показывает, что эти последовательности имеют один и тот же предел pj*:
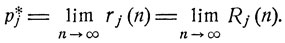
Очевидно,
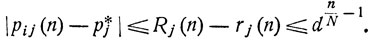
При любом начальном распределении pi0, i = 1, ..., m, имеем
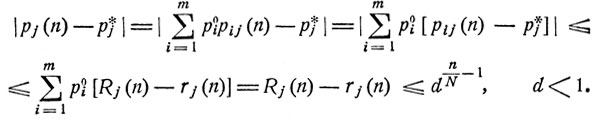
Полученные оценки, конечно, можно переписать в виде (8.14) при соответствующих постоянных С и D, полагая
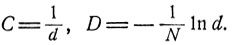
Теорема доказана.
Финальные вероятности pj*, j = 1, ...,m, являются решением следующей системы линейных уравнений:
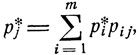
(8.15)
j = 1, ..., m.
Эти уравнения получаются, если в формуле (8.4), согласно которой
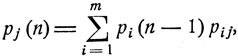
перейти к пределу при n→∞.
Рассмотрим произвольную цепь Маркова с состояниями ε1, ε2, ... и числа рi0, i = 1, 2 ..., такие, что
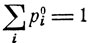
(8.16)
и
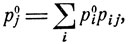
(8.17)
Взяв pi0, i = 1, 2, ..., в качестве начального распределения вероятностей, будем иметь следующие вероятности pj (n) для нахождения системы в соответствующих состояниях εj через n шагов:
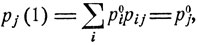
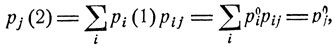
.........................................
Видно, что вероятности pj (n) остаются неизменными:
pj (n) = pj0, j = 1, 2, ...,
каково бы ни было n = 1, 2, ...
Цепь Маркова называется стационарной, если вероятности pj (n), j = 1, 2, ..., остаются неизменными при всех n = 0, 1, ...; стационарным называется и соответствующее распределение вероятностей pj0 = pj (n), j = 1, 2, ... Согласно формуле (8.4) распределение вероятностей рj0, j = 1, 2, ..., является стационарным тогда и только, тогда, когда оно удовлетворяет системе уравнений (8.17).
Если при любом начальном распределении существуют одни и те же финальные вероятности 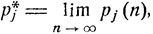 то стационарное распределение единственно:
то стационарное распределение единственно: 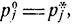 j = 1, 2,...
j = 1, 2,...
Полученные выше результаты могут быть соединены в следующую теорему.
Теорема. При условии (8.12) финальные вероятности pj*, j = 1, ..., m, являются единственным решением системы линейных уравнений (8.15), удовлетворяющим дополнительному требованию вида 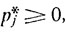
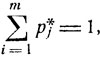 и образуют стационарное распределение вероятностей.
и образуют стационарное распределение вероятностей.
Остановимся на рассмотренных ранее (в пп. 1, 2) примерах.
Задача о стопке книг. Как показывают проведенные ранее расчеты, для m = 2 стационарное распределение вероятностей возникает уже на первом шаге:
p1 (n) = p1, р2 (n) = р2
при всех n = 1, 2, ... и любом начальном распределении вероятностей.
Рассмотрим случай произвольного m. Обозначим p(i1, ..., im),(j1, ..., jm) вероятность перехода из состояния (i1, ..., im) в состояние (j1, ..., jm). Как было показано,
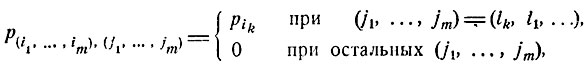
где перестановка (ik, i1, ...) получается из (i1, ..., im) выбором некоторого ik и перестановкой его на первое место. Финальные вероятности 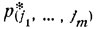 являются решением следующей системы линейных уравнений:
являются решением следующей системы линейных уравнений:
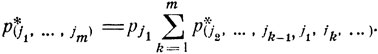
Через достаточно большое число шагов практически устанавливается стационарное распределение вероятностей, т. е. стопка книг будет с неизменными вероятностями 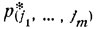 занимать соответствующие положения (i1, ..., im). Естественно спросить, с какой вероятностью каждая из имеющихся книг оказывается лежащей сверху?
занимать соответствующие положения (i1, ..., im). Естественно спросить, с какой вероятностью каждая из имеющихся книг оказывается лежащей сверху?
Вероятность того, что сверху лежит книга с номером i, есть, очевидно,
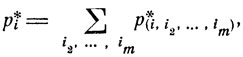
где берется сумма по всем состояниям, в которых на первом месте стоит i.
Из уравнений для финальных вероятностей получаем, что
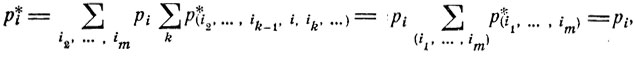
т. е. финальная вероятность р*i находиться сверху книге с номером i равна той вероятности рi с которой эта книга выбирается. Таким образом, чем чаще берется та или иная книга, тем с большей вероятностью она будет находиться сверху.
Случайные блуждания. Пусть блуждающая частица из каждой целочисленнной точки i переходит с одной и той же вероятностью р в соседнюю точку i+1, ас вероятностью q - в точку i-1.
При p<q или p>q частица с течением времени все дальше смещается в направлении -∞ или +∞ соответственно. При p = q, хотя она и будет бесконечное число раз возвращаться в каждое из состояний, но при любом фиксированном i вероятность pi (n) находиться в точке i в пределе при n→∞ равна 0.
Рассмотрим случайное блуждание, при котором частица с вероятностью pi переходит из точки i в соседнюю точку j = i+1, а с вероятностью qi = 1-pi - в точку j = 0.
Для невозвратных состояний, когда
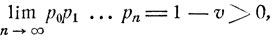
частица с вероятностью 1 будет уходить при n→☆ в направлении +∞ и, очевидно, никакого стационарного распределения быть не может. Распределение вероятностей является стационарным тогда и только тогда, когда оно удовлетворяет системе уравнений (8.17). В нашем случае эта система выглядит следующим образом:
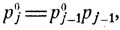
j = 1, 2, ...,
откуда

Видно, что стационарное распределение существует тогда и только тогда, когда сходится ряд
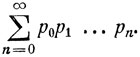
При этом, очевидно, стационарное распределение вероятностей имеет вид
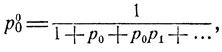
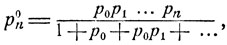
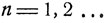
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'