§ 7. Производящие и характеристические функции. Предельные теоремы

1. Пусть ξ - целочисленная случайная величина, принимающая в зависимости от случайного исхода ω одно из значений 0, 1, 2, ... с соответствующими вероятностями

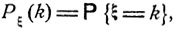
k = 0, 1, ...

Функция F_ξ (z) переменного z, 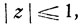вида

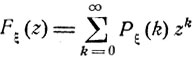
(7.0)

называется производящей функцией случайной величины ξ или соответствующего распределения вероятностей P_ξ (k), k = 0, 1, ...

F_ξ (z) является аналитической функцией от z и формула (7.0) дает ее разложение в степенной ряд. Ясно, что распределение вероятностей случайной величины ξ однозначно определяется ее производящей функцией F_ξ (z); в частности, по формуле Тейлора

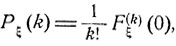
k = 0, 1,...

Согласно формуле (4.13) производящая функция F_ξ (z) при фиксированном z представляет собой не что иное, как математическое ожидание случайной величины φ(ξ) = z^ξ:

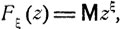
(7.1)

Пример.(Пуассоновское распределение.) Пусть случайная величина ξ имеет пуассоновское распределение вероятностей с параметром а:

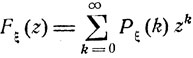
k = 0, 1, ...

Тогда ее производящая функция F_ξ (z) есть

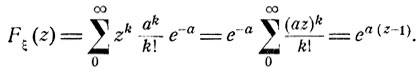
Пусть целочисленная величина ξ имеет математическое ожидание а = Мξ и дисперсию σ² = Dξ. Формально вычисляя производные функции F_ξ (z), дифференцируя по z под знаком математического ожидания, получаем

Эти соотношения могут быть легко обоснованы, если обратиться к свойствам степенных рядов. Именно, дифференцируя ряд (7.0) при 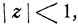получаем, что

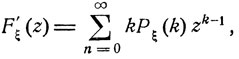
Откуда

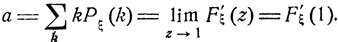
Совершенно аналогично устанавливается второе из соотношений (7.3).

Рассмотрим несколько целочисленных случайных величин ξ₁, ..., ξ_n. Предположим, что они являются независимыми. Тогда независимыми будут и величины z^ξ₁, ..., z^ξ_n (z - фиксированное число). Согласно общей формуле (4.22)

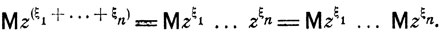
Видно, что производящая функция F_ξ (z) = Mz^ξ суммы ξ = ξ₁ + ... + ξ_n независимых случайных величин ξ₁, ..., ξ₁ выражается через производящие функции F_ξk (z) = Mz^ξ_k отдельных слагаемых ξ_k следующим образом:

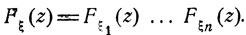
(7.4)

Пример. (Биномиальное распределение.) Пусть случайная величина ξ имеет биномиальное распределение вероятностей с параметрами (р, n):

Как уже отмечалось ранее (см. формулу (6.1)) ее можно 1 представить в виде суммы n независимых величин ξ_k, k = 1,..., n:

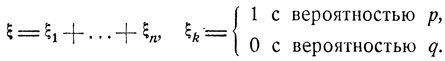
Производящая функция F_ξk (z) отдельного слагаемого, очевидно, равна pz + q, и по формуле (7.4) производящая функция F_ξ (z) величины ξ есть

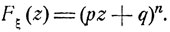
(7.5)

Рассмотрим, далее, последовательность случайных величин ξ₁, ξ₂, ... . Пусть P_n (k), k = 0, 1, ..., задают распределение вероятностей величины ξ_n с производящей функцией F_n (z): P_n (k) = P_ξn (k). Говорят, что последовательность распределений {P_n (k), k = 0, 1, ...}, n = 1, 2, ..., слабо сходится к предельному распределению вероятностей P(k), k = 0, 1, ..., если

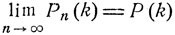
(7.6)

при всех k = 0, 1, ... ,

Пример. (Слабая сходимость биномиальных распределений к пуассоновскому.) Рассмотрим последовательность случайных величин ξ_n, n = 1, 2, ..., имеющих биномиальное распределение с соответствующими параметрами (р, n), где р зависит от n таким образом, что существует предел

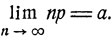
Как фактически было показано ранее (см. формулу (6.3)), последовательность таких биномиальных распределений {Р_n (k), k = 0, ..., n}, n = 1, 2, ...:

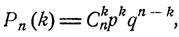
q = 1 - p,

слабо сходится к пуассоновскому распределению вероятностей P(k), k = 0, 1, ...:

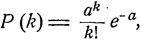
k = 0, 1, ...,

с параметром а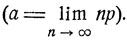

Отметим здесь, что последовательность производящих функций F_n (z) = (pz + q)ⁿ величин ξ_n (см. формулу (7.5)) равномерно сходится к производящей функции 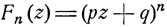предельного пуассоновского распределения:

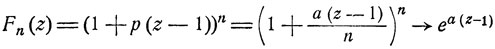
при n→∞.

Теорема. Слабая сходимость распределений вероятностей эквивалентна сходимости соответствующей последовательности производящих функций F_n (z):

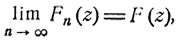
(7.7)

где 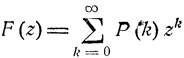- производящая функция предельного распределения вероятностей Р(k), k = 0, 1, ..., и сходимость является равномерной в каждом круге .

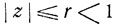Доказательство. Пусть выполнены предельные соотношения (7.6). Тогда, каково бы ни было K,

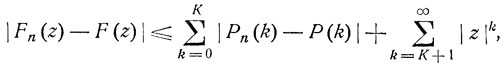
откуда видно, что для любого наперед заданного ε>0 можно выбрать столь большое К, что при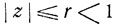

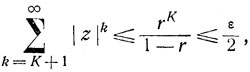
и такое N, что при k = 0, ..., К

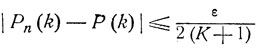
для n≥N. Отсюда заключаем, что при всех z,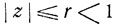

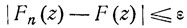
для n≥N.

Далее, согласно известной теореме Вейерштрасса, из равномерной сходимости аналитических функций F_n (z) вытекает сходимость их производных F_n^(k) (z), так что

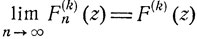
при любом z, 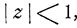каково бы ни было k, k = 0, 1, ... . Поскольку

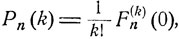
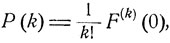
то и

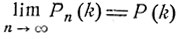
при любом k = 0, 1, ... Теорема доказана.

Рассмотрим один типичный пример возникновения распределения Пуассона.

Пример. Поток событий. Предположим, что с течением времени регистрируется наступление каких-либо событий (другими словами, имеется некоторый поток событий). Например, на некоторую систему обслуживания поступает поток требований (скажем, в справочное бюро поступают запросы, к бензозаправочной станции подъезжают автомашины и т. п.). В течение промежутка времени Δ осуществляется некоторое случайное число ξ(Δ) рассматриваемых событий. Спрашивается, каково распределение вероятностей случайных величин ξ(Δ)?

Предположим, что поток событий удовлетворяет следующим условиям. Во-первых, регистрируемые события независимы друг от друга, точнее, непересекающимся временным промежуткам Δ₁, Δ₂, ... отвечают независимые случайные величины ξ(Δ₁), ξ(Δ₂) ... . Во-вторых, рассматриваемый поток событий является стационарным, т. е. распределения вероятностей каждой из величин ξ(Δ) зависят лишь от длины соответствующего временного промежутка Δ. В-третьих, вероятность того, что за бесконечно малый промежуток времени Δt осуществится хотя бы одно событие, есть λ*Δt + o(Δt), а вероятность осуществления более чем одного события есть о(Δt), где о(Δt) - бесконечно малая высшего порядка по сравнению с Δt, а λ - некоторый положительный параметр, характеризующий "частоту" наступления событий.

Если разбить заданный интервал времени (0, t) на n равных частей Δ₁, ..., Δ_n, то общее число ξ (t) тех событий, которые наступают в интервале времени (0, t), будет

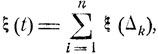
где ξ(Δ₁), ..., ξ(Δ_n) - независимые случайные величины, каждая из которых равна числу событий в соответствующем временном интервале Δ_k. Производящая функция каждой из величин ξ(Δ_k) с точностью до малых высшего порядка по сравнению с ¹/_n есть

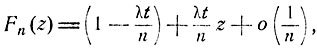
а производящая функция F (z) общего числа событий, согласно формуле (7.3), будет

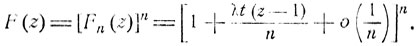
Переходя здесь к пределу при n→∞, получаем следующее К выражение для производящей функции F (z):

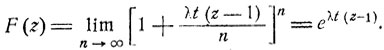
Видно (см. формулу (7.2)), что это есть производящая функция пуассоновского распределения с параметром a = λt, так что

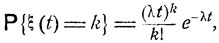
k = 0, 1, ..,

где введенная ранее постоянная λ есть среднее число событий, наступающих за единицу времени:

2. Характеристическая функция 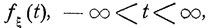произвольной действительной случайной величины ξ определяется как

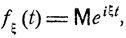
(7.8)

т. е. при каждом фиксированном t совпадает с математическим ожиданием комплексной случайной величины вида η = e^iξt.

Для целочисленной величины ξ значения характеристической функции f_ξ (t) совпадают со значениями производящей функции F_ξ (z) на границе единичного круга: f_ξ (t) = F_ξ (z) при z = e^it, или

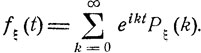
(7.9)

Эта формула дает разложение функции f_ξ (f) в ряд Фурье, коэффициенты которого совпадают с вероятностями Р_ξ (k) = Р {ξ = k}, k = 0, 1, ... . Таким образом, эти вероятности Р_ξ (k) однозначно определяются характеристической функцией f_ξ (t).

Для непрерывно распределенной величины ξ с плотностью распределения вероятностей р_ξ (х) характеристическая функция f_ξ (t) как это следует из общей формулы (4.19), представляет собой интеграл Фурье плотности р_ξ (х):

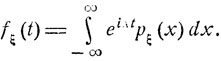
(7.10)

Как известно из анализа, всякая функция однозначно определяется своим интегралом Фурье, так что плотность р_ξ (х) однозначно определяется характеристической функцией f_ξ (t).

Пусть случайная величина ξ такова, что существует математическое ожидание 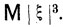Тогда для характеристической функции f_ξ (t) имеет место следующее разложение:

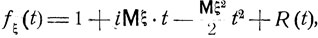
(7.11)

где для остаточного члена R (t) справедлива оценка:.

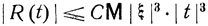
(здесь С - некоторая постоянная). Из разложения (7.11) следует, в частности, что математическое ожидание а = Мξ и дисперсия 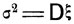могут быть подсчитаны по формулам

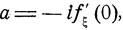
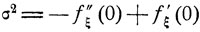
(7.12)

(ср. с формулами (7.3)).

Для доказательства (7.11) можно воспользоваться формулой Тейлора: при любом фиксированном ξ

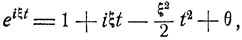
где

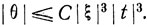
Взяв математическое ожидание обеих частей, получаем формулу (7.11).

Пусть ξ₁, ..., ξ_n - независимые случайные величины и ξ = ξ₁ + ... + ξ_n. Тогда по формуле (4.22) характеристическая функция f_ξ (t) суммы величин ξ₁, ..., ξ_n есть

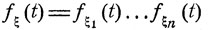
(7.13)

(ср. с формулой (7.4)).

Пусть имеется последовательность некоторых случайных величин ξ_n, n = 1, 2,..., с характеристическими функциями f_n (t), n = 1, 2... Говорят, что последовательность распределений вероятностей этих величин слабо сходится к распределению с плотностью р (х), если для любых х', х" (x'≤x")

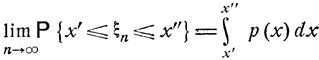
(7.14)

(ср. с данным ранее определением слабой сходимости для целочисленных величин ξ_n).

Теорема^*. Слабая сходимость распределений вероятностей эквивалентна сходимости соответствующей последовательности характеристических функций f_n (t):

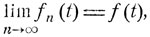
(7ю15)

где 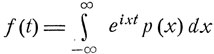- характеристическая функция предельного распределения вероятностей с плотностью р (х), и сходимость является равномерной в каждом конечном интервале t'≤t≤t".

^* (См., например, Б. В. Гнеденко, Курс теории вероятностей, изд. 4, М., 1965.)

Перейдем к так называемой центральной предельной теореме, очень частным случаем которой является предельная теорема Муавра - Лапласа (см. п. 2 § 6)^*.

^* (См., например, Б. В. Гнеденко, Курс теории вероятностей, изд. 4, М., 1965.)

Говорят, что независимые случайные величины ξ_k, k = 1,2..., имеющие конечные математические ожидания a_k = Mξ_k и дисперсии 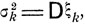удовлетворяют центральной предельной теореме, если для нормированных сумм

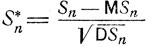
этих величин 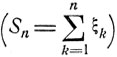выполняется предельное соотношение (6.7).

Центральная предельная теорема будет доказана ниже при так называемом условии Ляпунова:

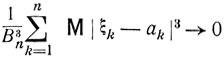
(7.16)

при n→∞, где

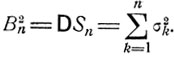
Отметим, что условие Ляпунова всегда выполняется для одинаково распределенных случайных величин ξ₁, ξ₂, ..., имеющих конечный третий момент 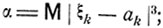именно,

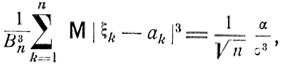
поскольку для независимых одинаково распределенных величин )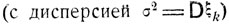

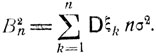
Грубо говоря, центральная предельная теорема означает, что случайные величины ξ, слагающиеся из большого числа малых "слабо зависимых" величин, имеют приблизительно нормальное распределение вероятностей:

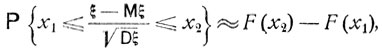
где F (x) определяется формулой (6.9).

Найдем характеристическую функцию f (t) нормального распределения с плотностью 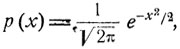используя тот факт, что, как для всякой плотности вероятности,

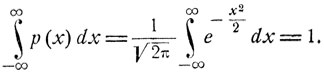
Имеем

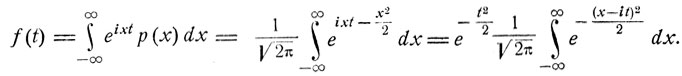
Функция 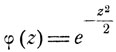как функция от комплексного переменного z является аналитической и интеграл по замкнутому контуру Прямоугольника с вершинами (- N, О), (N, О), (N, -it), (- N, - it) равен 0. Поэтому, как легко видеть,

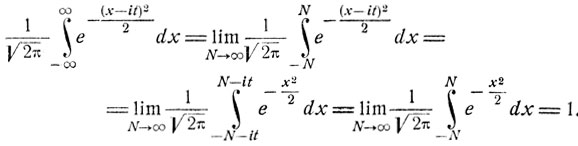
Таким образом, характеристическая функция нормального распределения есть

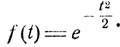
(7.17)

Если случайная величина ξ имеет указанное нормальное распределение вероятностей, то математическое ожидание а и дисперсия σ² суть (см. формулу (7.12))

Центральная предельная теорема означает слабую сходимость, распределений нормированных сумм S^*_n, n = 1, 2, ..., к нормальному распределению вероятностей:

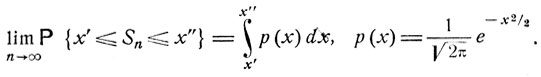
Согласно сформулированной выше теореме о слабой сходимости, достаточно доказать, что характеристические функции f_n (t) величин S^*_n при n→∞ сходятся к характеристической функции нормального распределения (равномерно в каждом конечном интервале t'≤t≤t"). Имеем

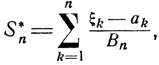
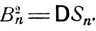
Случайные величины ξ_k - a_k имеют нулевые математические ожидания и дисперсии σ²_k и (по формуле 7.11) для их характеристических функций g_k (t) имеет место следующее разложение:

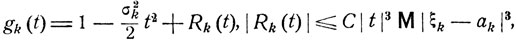
где С - некоторая постоянная. Характеристические функции f_kn (t) слагаемых 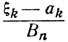суть

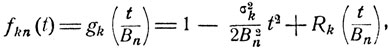
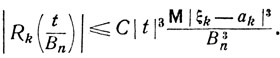
По формуле (7.13) характеристические функции fn(t) величин S*n есть

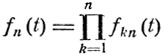
и

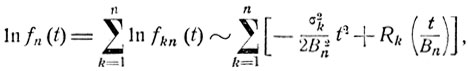
где по условию (7.16)

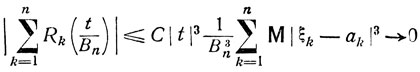
при n→∞ равномерно в каждом конечном интервале t'≤t≤t".

Таким образом,

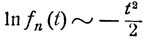
и при n→∞

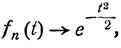
что и требовалось доказать.