
§ 6. Испытания Бернулли. Биномиальное и пуассоновское распределения. Теорема Муавра-Лапласа. Нормальное распределение вероятностей
1. Одинаковые, независимые между собой испытания, в каждом из которых рассматривается некоторое событие А, наступающее с положительной вероятностью р = Р (А), называются испытаниями Бернулли. Само событие А условно называется "успехом", а дополнительное событие 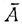 , наступающее в каждом из рассматриваемых испытаний с вероятностью q = 1-р, условно называется "неудачей".
, наступающее в каждом из рассматриваемых испытаний с вероятностью q = 1-р, условно называется "неудачей".
Если рассматривается n испытаний, то каждый элементарный исход ω может быть описан, например, последовательностью длины n из 1 и 0 вида 10110001..., где стоящая на i-м месте 1 означает "успех" при i-м испытании, а 0 означает "неудачу". Вероятность Р (ω) элементарного исхода ω, при котором ровно k раз наступает "успех" и n - k раз наступает "неудача", в силу независимости отдельных испытаний есть
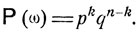
Видно, что элементарные исходы ω не являются равновероятными, когда р≠q.
Рассмотрим случайную величину ξ, равную общему числу "успехов" в n испытаниях Бернулли: 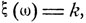 если при элементарном исходе ω ровно k раз наступает "успех". Различных исходов ω, приводящих к одному и тому же числу k "успехов", столько же, сколько можно образовать различных комбинаций из k единиц и n - k нулей. Число таких комбинаций равно числу сочетаний из n по k, что составляет
если при элементарном исходе ω ровно k раз наступает "успех". Различных исходов ω, приводящих к одному и тому же числу k "успехов", столько же, сколько можно образовать различных комбинаций из k единиц и n - k нулей. Число таких комбинаций равно числу сочетаний из n по k, что составляет 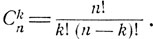 Все. эти исходы со имеют одну и ту же вероятность
Все. эти исходы со имеют одну и ту же вероятность 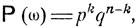 так что событие
так что событие 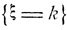 имеет вероятность
имеет вероятность 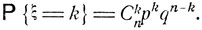 Таким образом, распределение вероятностей случайной величины ξ задается формулой
Таким образом, распределение вероятностей случайной величины ξ задается формулой
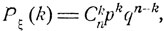
k = 0, ..., n. (6.0)
Это - так называемое биномиальное распределение. Оно задается двумя параметрами: вероятностью отдельного "успеха" р и числом испытаний n.
Полезно отметить, что случайная величина ξ есть сумма n независимых величин ξ1, ..., ξn, определяемых следующим образом: ξk = 1, если в k-м испытании наступает "успех", и ξk = 0, если наступает "неудача":
ξ = ξ1 + ... + ξn.(6.1)
Имеем
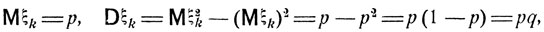
откуда для математического ожидания и дисперсии случайной величины ξ получаем следующие выражения:
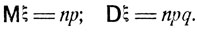
(6.2)
При большом числе испытаний п и сравнительно малой вероятности р, когда каждый из "успехов" является сравни-| тельно редким событием, но среднее число "успехов" пр I довольно значительно, приблизительно можно считать, что
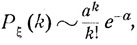
(6.3)
k = 0, 1, ...,
где а = nр есть среднее число "успехов", а е = 2,78... - основание натуральных логарифмов.
В самом деле, как хорошо известно из анализа, при любом фиксированном а
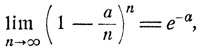
и поскольку 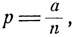 из формулы (6.0) получаем, что
из формулы (6.0) получаем, что
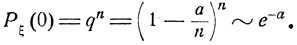
Как легко подсчитать,
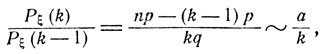
k = 1, 2, ...,
при n→∞. Следовательно,
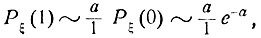
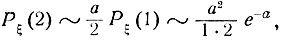
..................................................
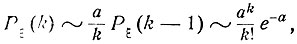
и, таким образом, приближенная формула (6.3) установлена.
Говорят, что случайная величина ξ (принимающая лишь целочисленные значения 0, I, ...) имеет пуассоновское распределение вероятностей (распределена по закону Пуассона), если
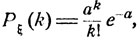
(6.4)
k = 0, 1, ...
Это распределение задается одним-единственным неотрицательным параметром а, совпадающим со средним значением Mξ:
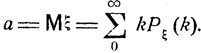
(6.5)
Действительно, воспользовавшись разложением 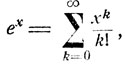 справедливым при всех х, имеем
справедливым при всех х, имеем
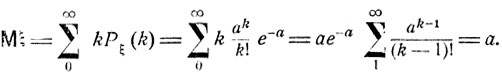
Приближенная формула (6.3) показывает, что при больших n и малых р случайная величина ξ, равная числу "успехов" в n испытаниях Бернулли (с вероятностью успеха р), приблизительно распределена по закону Пуассона с параметром а = nр.
Пример. Задача о лотерейных билетах. Сколько нужно купить лотерейных билетов, чтобы вероятность выигрыша была не меньшей, чем Р?
Пусть общее количество лотерейных билетов равно N и M - общее количество выигрышей. Тогда вероятность того, что купленный лотерейный билет окажется из числа М выигрышных билетов, равна 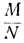 Приобретение каждого отдельного билета можно рассматривать как отдельное испытание с вероятностью "успеха"
Приобретение каждого отдельного билета можно рассматривать как отдельное испытание с вероятностью "успеха" 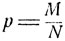 серии из n независимых испытаний (n - число купленных билетов). Если считать, что вероятность р мала, как это обычно бывает, а заданная вероятность Р сравнительно велика, то ясно, что нужно купить довольно большое число лотерейных билетов, чтобы вероятность хотя бы одного выигрыша была не меньше Р. Поэтому случайное число выигрышных билетов приблизительно распределено по закону Пуассона, т. е. вероятность того, что среди купленных n билетов окажется 1 ровно k выигрышных, есть
серии из n независимых испытаний (n - число купленных билетов). Если считать, что вероятность р мала, как это обычно бывает, а заданная вероятность Р сравнительно велика, то ясно, что нужно купить довольно большое число лотерейных билетов, чтобы вероятность хотя бы одного выигрыша была не меньше Р. Поэтому случайное число выигрышных билетов приблизительно распределено по закону Пуассона, т. е. вероятность того, что среди купленных n билетов окажется 1 ровно k выигрышных, есть
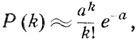
где 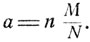 Вероятность того, что хотя бы один из билетов будет выигрышным, есть
Вероятность того, что хотя бы один из билетов будет выигрышным, есть 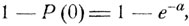 так что число n нужно определить как наименьшее целое число, для которого
так что число n нужно определить как наименьшее целое число, для которого
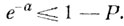
Задача об изюминках. Имеется некоторое количество теста V, из которого выпекаются булочки с изюмом. Некоторое количество изюма n высыпается в тесто, после чего все многократно тщательно перемешивается и затем разрезается на равные части. Скажем, на отдельную булку расходуется количество теста v, так что всего выпекается 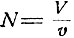 булок с изюмом. Ясно, что, хотя средний расход изюма на отдельную булку составляет вполне определенную величину
булок с изюмом. Ясно, что, хотя средний расход изюма на отдельную булку составляет вполне определенную величину 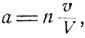 количество изюма в разных булках вовсе не одинаково. Какова вероятность того, что в отдельно В взятой, случайно выбранной булке окажется хотя бы одна изюминка?
количество изюма в разных булках вовсе не одинаково. Какова вероятность того, что в отдельно В взятой, случайно выбранной булке окажется хотя бы одна изюминка?
Естественно считать, что количество изюма много меньше количества теста, так что при многократном перемешивании теста изюминки в конце концов движутся практически независимо друг от друга, в частности, независимо друг от 1 друга попадают или не попадают в выбранную булку. Очевидно, после тщательного перемешивания изюминки распределяются в тесте приблизительно равномерно, так что вероятность попадания любой из изюминок в любую из булок одна и та же и есть 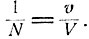
Попадание отдельной изюминки в определенную булку можно рассматривать как "успех" в отдельном испытании, вероятность которого есть 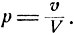 Независимость движения изюминок при перемешивании позволяет считать, что имеется n испытаний Бернулли с вероятностью "успеха" р, n - общее число изюминок. Эта вероятность сравнительно мала, если булок выпекается достаточно много. В то же время число изюминок n сравнительно велико. Следовательно, случайное число изюминок в отдельной булке, равное числу "успехов", приблизительно распределено по закону Пуассона: вероятность Р (k) того, что в булке окажется ровно k изюминок, есть
Независимость движения изюминок при перемешивании позволяет считать, что имеется n испытаний Бернулли с вероятностью "успеха" р, n - общее число изюминок. Эта вероятность сравнительно мала, если булок выпекается достаточно много. В то же время число изюминок n сравнительно велико. Следовательно, случайное число изюминок в отдельной булке, равное числу "успехов", приблизительно распределено по закону Пуассона: вероятность Р (k) того, что в булке окажется ровно k изюминок, есть
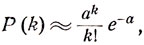
где 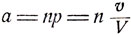 - среднее число изюминок, приходящихся на одну булку. Вероятность Р того, что в булке окажется хотя бы одна изюминка, есть
- среднее число изюминок, приходящихся на одну булку. Вероятность Р того, что в булке окажется хотя бы одна изюминка, есть
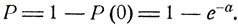
Модель радиоактивного распада. Как известно, радий Ra с течением времени превращается в радон Rn. Распадающееся ядро атома радия "испускает" так называемую α-частицу (ядро атома гелия Не). Установим некоторые закономерности, которым подчиняется процесс излучения радием α-частиц. Междуатомные расстояния сравнительно велики, и естественно считать, что распад отдельного атома радия происходит совершенно независимо от состояния других атомов. Предположим, что вероятность распада отдельного атома радия в некотором промежутке времени зависит лишь от длины этого промежутка. Обозначим p(t) вероятность распада в течение промежутка времени длины t Если в наличии имеется n атомов радия (в одном грамме насчитывается приблизительно 1022 атомов), то среднее число а-частиц, испускаемых за время t, будет a(t) = np(t). Как показывают многочисленные эксперименты, это число при t = 1 сек по порядку составляет 1010, так что вероятность p(t) является очень малой (при t = 1 сек вероятность p(t) по порядку равна 10-12).
Если считать "успехом" распад каждого из атомов радия, то число испускаемых за время t α-частиц будет равно числу "успехов" в n≈1022 "испытаний Бернулли" с вероятностью "успеха" p≈10-12. Параметры n и p таковы, что фактическим распределением вероятностей случайной величины ξ (t) - числа испускаемых за время t α-частиц - будет распределение Пуассона с параметром а = np:
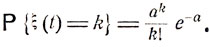
Здесь испытания Бернулли выступают как вспомогательная схема, позволяющая найти фактическое распределение случайной величины ξ (t) (которое оказывается пуассоновским).
Типичный пример возникновения пуассоновского распределения вероятностей будет рассмотрен ниже (см. п. 1 § 7).
2. Ранее уже отмечалось, что случайная величина ξ, равная числу "успехов" в n испытаниях Бернулли, совпадает с суммой n независимых величин ξ1, ..., ξn (см. формулу (6.1)). Введем новое обозначение, положив
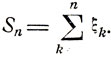
Пусть
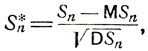
(6.6)
где MSn = np и DSn = npq. Имеет место следующее предельное соотношение, называемое предельной теоремой Муавра - Лапласа:
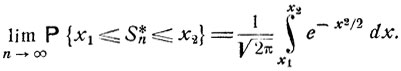
(6.7)
Фигурирующее здесь непрерывное распределение вероятностей с плотностью
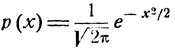
(6.8)
называется нормальным, или гауссовским, распределением. Как функция от х, плотность р (х) этого распределения вероятностей имеет график весьма специфической колоколообразной формы (рис. 8, а).
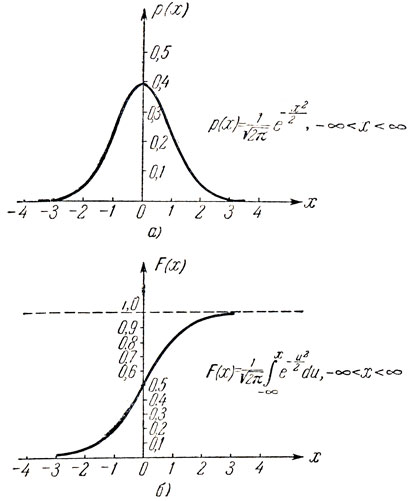
Рис. 8
Имеются* таблицы функции нормального распределения (рис. 8, б)
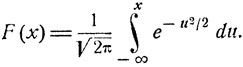
* (См., например, Л. Д. Мешалкин, Сборник задач по теории вероятностей, М., 1963.)
Перейдем к доказательству теоремы Муавра - Лапласа.
Нормированная величина Sn* в зависимости от случая принимает одно из значений х вида
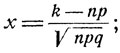
k = 0, ..., n,
разбивающих отрезок 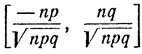 на равные промежутки длины
на равные промежутки длины
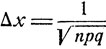
и при этом
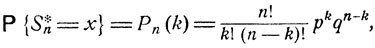
k = 0, ..., n.
Очевидно, при n→∞
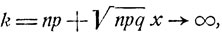
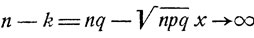
равномерно по х, х1#8804;х≤х2. Используя формулу Стирлинга, получаем, что
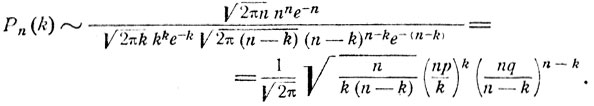
Далее,
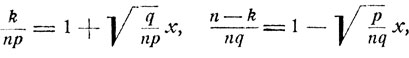
и, воспользовавшись разложением
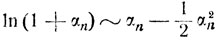
(при αn→0), получаем, что
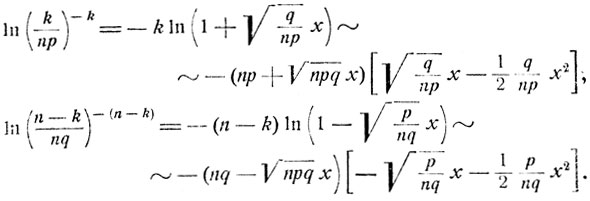
Складывая эти выражения, приходим к следующему соотношению:
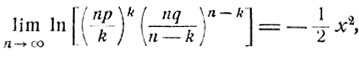
и, следовательно,
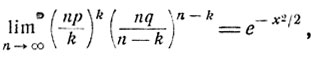
причем равномерно по х, x1≤x≤x2.
Далее,
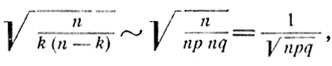
и в итоге получаем, что
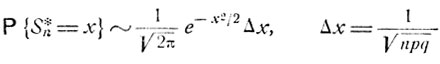
равномерно по всем 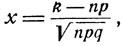 x1≤x≤x2 Следовательно,
x1≤x≤x2 Следовательно,
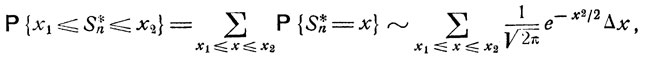
откуда легко вытекает предельное соотношение (6.7). Теорема доказана.
Процесс броуновского движения. Представьте себе мелкую частицу, взвешенную в однородной жидкости. Частица испытывает хаотические столкновения с молекулами жидкости, в результате чего она находится в непрерывном беспорядочном движении.
Дискретным аналогом этого процесса может служить следующая модель случайного блуждания. Частица меняет свое положение лишь в дискретные моменты времени, кратные Δt. Изменение положения происходит таким образом, что, находясь в точке х, частица, независимо от предшествующего поведения, переходит с равными вероятностями в одну из соседних точек х + Δх или х - Δх, причем смещение Δх одно и то же для всех точек х (речь идет лишь об одной координате движущейся частицы, иначе, об одномерном случайном блуждании). В пределе, когда Δt→0, Δx→0, получается непрерывное случайное блуждание, характерное для физического процесса броуновского движения.
Обозначим ξ (t) положение броуновской частицы в момент времени t. Пусть в начальный момент времени t = 0 частица находится в точке х = 0. При дискретном блуждании за время t она совершает 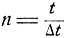 шагов, из которых какое-то случайное число шагов совершается в положительном направлении. Если обозначить Sn число шагов в положительном направлении, то общее смещение в положительном направлении составит SnΔх, а в отрицательном направлении - (n - Sn)Δx. Таким образом, общее смещение ξ(t) за время t = n*Δt связано с числом Sn следующим равенством:
шагов, из которых какое-то случайное число шагов совершается в положительном направлении. Если обозначить Sn число шагов в положительном направлении, то общее смещение в положительном направлении составит SnΔх, а в отрицательном направлении - (n - Sn)Δx. Таким образом, общее смещение ξ(t) за время t = n*Δt связано с числом Sn следующим равенством:
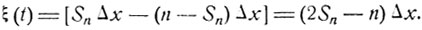
Если считать, что ξ (0) = 0, то
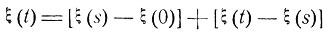
для любого s, 0≤s≤t Очевидно, в описанной модели случайного блуждания величины ξ(s) - ξ(0) и ξ(t) - ξ(s) являются независимыми, причем распределение вероятностей приращения ξ(t) - ξ(s) точно такое же, как и приращения ξ(t - s) - ξ(0). Поэтому дисперсия σ2(t) = Dξ(t) удовлетворяет соотношению
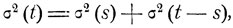
0≤s≤t.
Видно, что, как функция от t, дисперсия σ2(t) с ростом t меняется линейно и, таким образом,
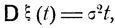
где σ2 - некоторая постоянная, называемая коэффициентом диффузии. С другой стороны, легко подсчитать, что дисперсия смещения за время t 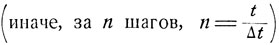 ) есть
) есть 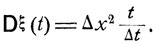 В итоге получаем следующее соотношение между Δх и Δt?
В итоге получаем следующее соотношение между Δх и Δt?
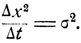
Совершаемые частицей переходы не зависят друг от друга, и их можно рассматривать как испытания Бернулли с вероятностью "успеха" 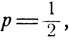 за который можно принять шаг в положительном направлении. Тогда Sn - число шагов в положительном направлении - будет равно числу "успехов" в n испытаниях Бернулли. При этом положение частицы в момент времени t будет следующим образом связано с нормированной величиной
за который можно принять шаг в положительном направлении. Тогда Sn - число шагов в положительном направлении - будет равно числу "успехов" в n испытаниях Бернулли. При этом положение частицы в момент времени t будет следующим образом связано с нормированной величиной 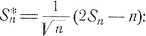
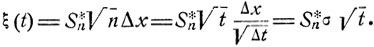
Используя теорему Муавра - Лапласа (см. соотношение (6.7)), получаем, что распределение вероятностей случайной величины ξ(t) при предельном процессе броуновского движения задается формулой
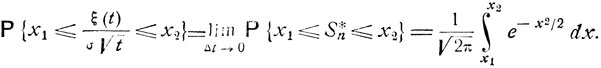
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'