§ 5. Среднеквадратичное значение и неравенство Чебышева. Дисперсия. Коэффициент корреляции. Закон больших чисел. Вероятность и частота

1.Среднеквадратичным значением случайной величины ξ называется математическое ожидание Мξ²:

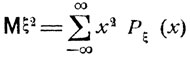
для дискретных величин,

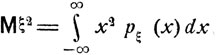
для непрерывно распределенных величин. Имеет место следующее неравенство Чебышева: каково бы ни было ε>0, имеет место неравенство

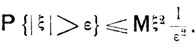
(5.0)

Его легко можно вывести из неравенства (4.16). В самом деле, если положить

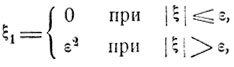
то, очевидно, ξ₁≤ξ² и

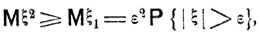
Кто и равносильно неравенству (5.0).

Неравенство Чебышева показывает, что если среднеквадратичное значение Мξ² мало по сравнению с ε²: ^Mξ2/_ε²≤δ практически можно пренебречь возможностью осуществления события 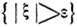малой вероятности (≤δ), то будет малой и сама случайная величина 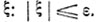В частности, если Мξ² = 0, то с вероятностью 1 и ξ = 0.

Дисперсией случайной величины ξ, обозначаемой Dξ, называется среднеквадратичное значение 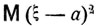разности ξ - а, где а = Mξ - математическое ожидание случайной величины ξ. Имеет место следующая формула:

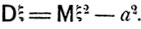
(5.1)

B самом деле,

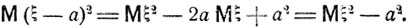
Очевидно,

и для любой постоянной с

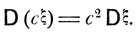
(5.2)

Пусть ξ₁ и ξ₂ - независимые случайные величины. Тогда дисперсия их суммы может быть найдена по формуле

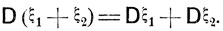
(5.3)

Действительно, если положить a₁ = Mξ₁ и a₂ = Mξ₂, то, согласно соотношению (4.17), будем иметь

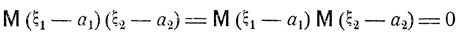
и

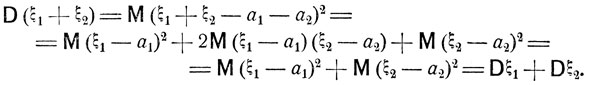
Рассмотрим случайные величины ξ₁ и ξ₂. Поставим следующую задачу: найти комбинацию вида сˆ₁ + сˆ₂ξ₂, где с ˆ₁ и сˆ₂ - некоторые постоянные, дающие наилучшее приближение для случайной величины ξ₁, наилучшее в том смысле, что

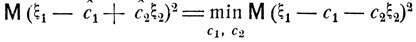(5.4)

(минимум берется по всем с₁ и с₂). Положим

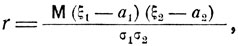
(5.5)

где

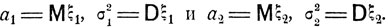
Перейдем для удобства к нормированным случайным величинам

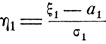
и

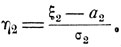
Очевидно,

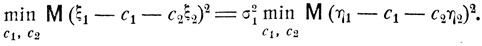
Имеем

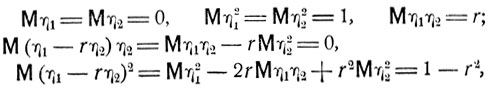
и для любых постоянных c₁ и c₂

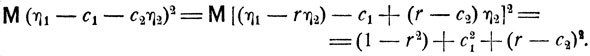
Видно, что минимум выражения М (η₁ - c₁ - c₂η₂)² достигается, когда с₁ = 0 и с₂ = r:

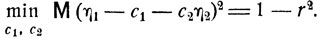
При переходе к исходным величинам ξ₁ и ξ₂ имеем

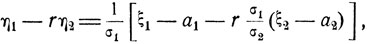
так что искомая линейная комбинация 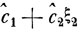в (5.4) есть

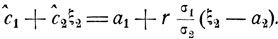
Здесь а₁ и а₂ - математические ожидания случайных величин ξ₁ и ξ₂, σ₁² и σ₂² - их дисперсии, а определенная равенством (5.5) постоянная r - так называемый коэффициент корреляции этих случайных величин.

Коэффициент корреляции r является простейшей характеристикой связи случайных величин ξ₁ и ξ₂. Если случайные величины ξ₁ и ξ₂независимы, то в силу соотношения (4.17)

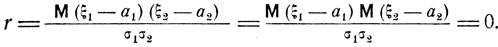
Как видно из формулы (5.6), коэффициент корреляции 1 всегда лежит в пределах

причем, если

то случайная величина ξ₁ есть просто линейная комбинация к вида

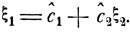
(5.10)

Действительно, если r = 1 или r = -1, то, согласно формуле (5.6), среднеквадратичное значение величины ξ₁ - c₁ˆ - c₂ˆξ₂ есть

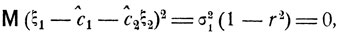
и, следовательно, ξ₁ - c₁ˆ - c₂ˆξ₂ = 0 с вероятностью 1.

2. Рассмотрим независимые случайные величины ξ₁, ..., ξ_n, имеющие одинаковое распределение вероятностей (и, в частности, одинаковые математические ожидания а = Мξ_k и дисперсии σ² = Dξ_k; k = 1, ..., n). Рассмотрим среднее арифметическое значение этих величин

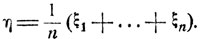
Имеем

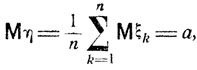
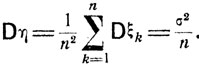
Используя неравенство Чебышева, получаем

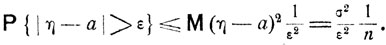
Очевидно, что, каково бы ни было δ>0, при достаточно большом n 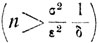среднее арифметическое 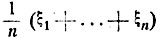величин ξ₁, ..., ξ_n с вероятностью, не меньшей 1 - δ, будет содержаться в пределах

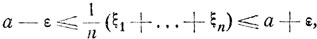
(5.11)

где ε>0 может быть заранее выбрано сколь угодно малым.

Этот факт носит название закона больших чисел. Если ε и δ столь малы, что можно практически пренебречь возможностью наступления события вероятности δ и различием величин, отличающихся друг от друга не более чем на ε, то практически можно считать, что, несмотря на случайность, среднее арифметическое 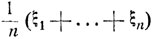практически совпадает с математическим ожиданием (средним значением) а = Mξ_k.

Предположим, что проводится серия одинаковых и независимых между собой опытов, в каждом из которых рассматривается некоторое событие А. Пусть n - число испытаний, n (А) - число тех из них, в которых осуществляется событие A, и 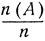- частота этого события в рассматриваемой серии испытаний. С каждым отдельным опытом можно связать случайную величину ξ_k (k - порядковый номер соответствующего испытания) вида

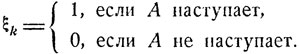
Ясно, что величины ξ₁, ..., ξ_n независимы и имеют одинаковое распределение вероятностей:

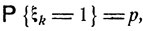
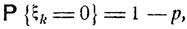
где р = Р (А). Очевидно, что

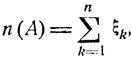
и, таким образом, частота события А совпадает со средним арифметическим

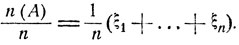
Математическое ожидание а = Мξ_k совпадает с вероятностью а = Р (А):

Согласно закону больших чисел при достаточно большом числе испытаний n можно практически считать, что частота 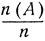события А совпадает с его вероятностью Р (А), точнее, как бы ни были малы ε>>0 и δ>0, при достаточно больших n с вероятностью, не меньшей 1-δ, частота 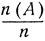будет отличаться от Р (А) не больше чем на ε:

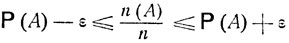
(5.12)

(см. по этому поводу п. 1 § 1).

Более того, можно доказать^*, что при n→∞ с вероятностью 1 существует предел 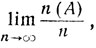совпадающий с вероятностью Р (А).

^* (См., например, Б. В. Гнеденко, Курс теории вероятностей, изд. 4-е, М., 1965.)