
§ 4. Общая теоретико-вероятностная схема. Случайные величины и распределения вероятностей. Математические ожидания
1. Результаты и методы современной теории вероятностей основываются на нескольких простых предположениях. Будем считать, что имеется некоторое пространство Ω элементарных исходов ω.
Допустим, что для рассматриваемых событий А (каждое из которых отождествляется с некоторой совокупностью элементарных исходов ω определены вероятности Р (А):
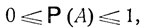
причем невозможное событие А = ∅ имеет вероятность 0, а достоверное событие А = Ω имеет вероятность 1.
Предполагается, что если определены вероятности каких-либо событий А1, A2, ... (взятых в конечном или счетном числе), то определены и вероятности всевозможных событий, получающихся из A1, A2, ... операциями объединения, пересечения, нахождения разности и перехода к дополнительным событиям; при этом в случае непересекающихся событий А1, А2, ... вероятность их объединения 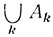 удовлетворяет равенству
удовлетворяет равенству
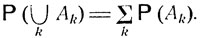
(4.0)
Следствием этого закона сложения вероятностей является свойство непрерывности: если 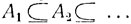 - "монотонно возрастающая" последовательность событий, т. е. такая, что каждое последующее событие содержит предыдущее, то
- "монотонно возрастающая" последовательность событий, т. е. такая, что каждое последующее событие содержит предыдущее, то
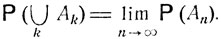
(4.1)
В самом деле, событие 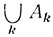 совпадает с объединением непересекающихся событий B1 = A1, B2 = A2\B1, ...,
совпадает с объединением непересекающихся событий B1 = A1, B2 = A2\B1, ..., 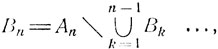 причем объединение только событий B1, ..., Вn совпадает с Аn. В силу закона сложения вероятностей
причем объединение только событий B1, ..., Вn совпадает с Аn. В силу закона сложения вероятностей
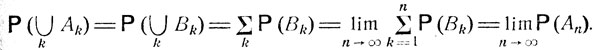
Аналогично, если 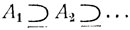 "монотонно убывающая" последовательность событий, т. е. такая, что каждое последующее событие содержится в предыдущем, то
"монотонно убывающая" последовательность событий, т. е. такая, что каждое последующее событие содержится в предыдущем, то
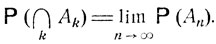
В самом деле, если перейти к дополнительным событиям  1
1
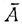 2
2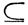 ..., то, согласно только что установленному свойству непрерывности,
..., то, согласно только что установленному свойству непрерывности,
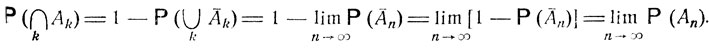
`
Следует отметить, что для любых событий А1, A2, ... вероятность их объединения такова, что
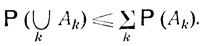
(4.3)
В самом деле, событие 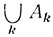 совпадает с объединением непересекающихся событий B1 = A1, B2 = A2\B1 ...,
совпадает с объединением непересекающихся событий B1 = A1, B2 = A2\B1 ..., 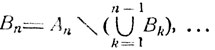 и потому
и потому
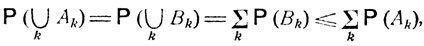
поскольку 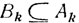 и
и (см. неравенство (2.1)).
(см. неравенство (2.1)).
Пример. (Леммы Бореля - Кантелли.) Предположим, что рассматривается некоторая последовательность событий А1, А2, ... Пусть В означает, что происходит бесконечное число событий из А1, A2, ... Какова вероятность Р (B)?
На этот вопрос легко ответить в случае, когда вероятности pk = Р (Ak) рассматриваемых событий достаточно быстро убывают и
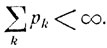
Положим 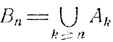 означает, что происходит хотя бы одно событие из Аn, Аn+1, ...). Ясно, что если происходит бесконечное число событий из А1, А2, ..., то наступает каждое из Вn, n = 1, 2, ... С другой стороны, если осуществляется каждое из событий Вn, то наступает и событие В. Таким образом,
означает, что происходит хотя бы одно событие из Аn, Аn+1, ...). Ясно, что если происходит бесконечное число событий из А1, А2, ..., то наступает каждое из Вn, n = 1, 2, ... С другой стороны, если осуществляется каждое из событий Вn, то наступает и событие В. Таким образом,
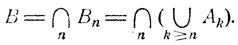
Очевидно, 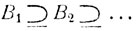 и согласно свойству непрерывности,
и согласно свойству непрерывности,
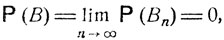
поскольку в силу сходимости ряда 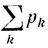
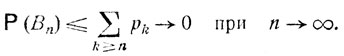
при n→∞.
Полученный ответ можно переформулировать следующим образом: если ряд 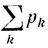 сходится, то с вероятностью может произойти лишь конечное число событий из последовательности A1, A2, ...
сходится, то с вероятностью может произойти лишь конечное число событий из последовательности A1, A2, ...
Найдем теперь вероятность Р (В) в случае, когда ряд 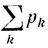 расходится, т. е. когда
расходится, т. е. когда
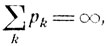
предположив дополнительно, что события A1, A2, ... являются взаимно независимыми.
Для дополнительных событий имеем
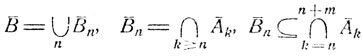
и для каждого отдельного события 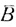 n
n
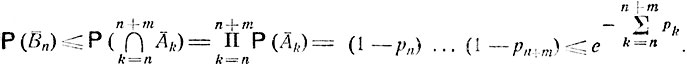
В этих оценках использовано неравенство вида 1-х≤e-x, x≥0, и произвольно взятое целое m≥0. Из расходимости ряда 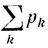 вытекает, что
вытекает, что 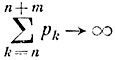 при m→∞, так что полученная при любом m оценка вероятности Р (
при m→∞, так что полученная при любом m оценка вероятности Р ( n) означает, что на самом деле Р (
n) означает, что на самом деле Р (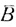 n) = 0 для каждого n = 1, 2, ... Следовательно,
n) = 0 для каждого n = 1, 2, ... Следовательно,
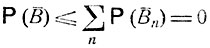
и

Полученный ответ можно сформулировать следующим образом: если ряд 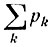 расходится, то с вероятностью 1 происходит бесконечное число из последовательности независимых событий A1, А2, ...
расходится, то с вероятностью 1 происходит бесконечное число из последовательности независимых событий A1, А2, ...
2. Числовая величина ξ, значения которой зависят от элементарных исходов 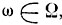 называется случайной величиной:
называется случайной величиной:
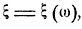
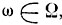
Говорят, что задано распределение вероятностей случайной величины ξ, если определены вероятности 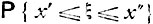 всевозможных событий
всевозможных событий 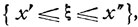 каждое из которых означает, что ξ принимает одно из значений
каждое из которых означает, что ξ принимает одно из значений 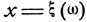 в соответствующих пределах
в соответствующих пределах 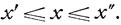
Случайная величина ξ имеет дискретное распределение (иначе, величина ξ является дискретной), если в зависимости от элементарных исходов ω величина 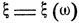 принимает конечное или счетное число различных значений х с соответствующими вероятностями Рξ (х):
принимает конечное или счетное число различных значений х с соответствующими вероятностями Рξ (х):
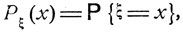
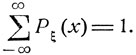
Для таких величин
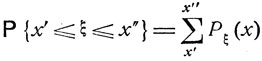
(4.4)
(суммирование идет по конечному или счетному числу значений х в пределах 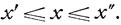 которые может принять дискретная случайная величина ξ).
которые может принять дискретная случайная величина ξ).
Говорят, что 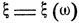 имеет непрерывное распределение вероятностей, если для любых х' и х" (х'≤х")
имеет непрерывное распределение вероятностей, если для любых х' и х" (х'≤х")
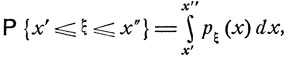
(4.5)
где рξ(х) - некоторая неотрицательная интегрируемая функция,
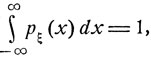
называемая плотностью распределения вероятностей величины ξ.
Легко видеть, что если случайная величина ξ имеет непрерывное распределение вероятностей, то для каждого отдельного значения х
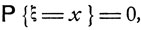
и для каждой точки х, в которой плотность распределения рξ(х) непрерывна,
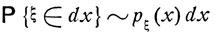
(здесь 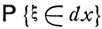 - вероятность события
- вероятность события 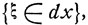 означающего, что величина ξ принимает значения из бесконечно малого интервала dx с центром в точке х).
означающего, что величина ξ принимает значения из бесконечно малого интервала dx с центром в точке х).
Определенная как
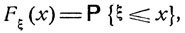
(4.6)
-∞<x<∞
функция Fξ (х) называется функцией распределения случайной величины ξ. Для дискретной величины ξ функция распределения Fξ (x) является ступенчатой, принимая конечное или счетное число различных значений:
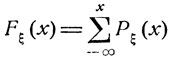
(на рис. 4, а изображен график функции такого типа).
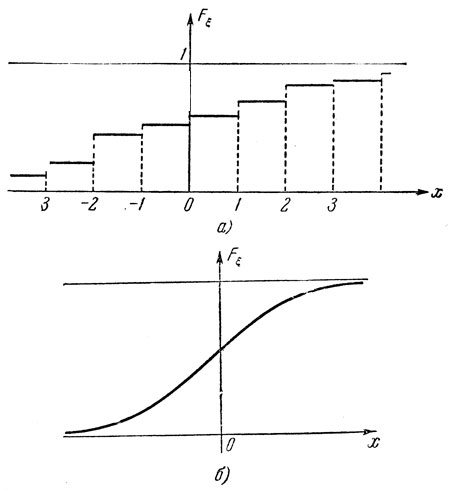
Рис. 4. а) Вид функции распределения вероятностей некоторой случайной величины ξ, принимающей лишь целые значения х = ..., - 3, - 2,..., 2, 3, ... Скачки функции Fξ (х) в целых точках х = -3, -2, ..., 2, 3, ... но величине равны соответствующим вероятностям Рξ (х). б) Вид непрерывной функции распределения. Любая непрерывная монотонная функция Fξ (х) такая, что
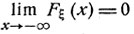 и
и 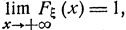 может быть функцией распределения вероятностей некоторой случайной величины ξ
может быть функцией распределения вероятностей некоторой случайной величины ξДля непрерывно распределенной величины ξ функция распределения Fξ (x) имеет своей производной плотность рξ(х), точнее,
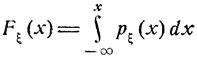
(функция такого типа изображена на рис. 4, б).
Для любой случайной величины ξ
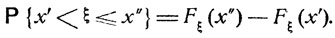
(4.7)
Совместное распределение вероятностей. Рассмотрим случайные величины ξ1 и ξ2 или, как еще говорят, векторную случайную величину ξ = (ξ1, ξ2).
Для дискретных случайных величин (ξ1, ξ2) определяются вероятности
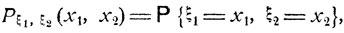
где x1, х2 пробегают всевозможные значения соответствующих величин ξ1, ξ2. Вероятность всякого события типа {(ξ1, ξ2)∈B} - "случайная точка (ξ1, ξ2) попадает в заданную область В" - задается формулой
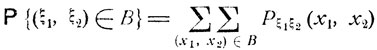
(4.8)
(суммирование идет по всем возможным значениям х1, х2 случайных величин ξ1, ξ2, таким, что соответствующая точка (x1, х2) входит в область В).
Плотностью совместного распределения вероятностей непрерывно распределенных случайных величин ξ1, и ξ2 называется такая функция pξ1 ξ2 (x1, x2) переменных х1 и x2, что вероятность всякого события типа {(ξ1, ξ2)∈ В} задается формулой
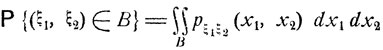
(4.9)
(интегрирование идет по области В).
Случайные величины ξk, k = 1, 2,..., называются независимыми, если при любых x'k и x"k независимыми являются события вида {x'k≤ξk≤x"k}, k = 1, 2, ...
Предположим, что рассматриваются различные группы независимых случайных величин ξ1, ξ2, ..., скажем,
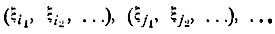
(каждая из величин ξ1, ξ2, ..., входит лишь в одну из рассматриваемых групп); тогда случайные величины η1, η2, ..., где η1 является какой-либо функцией от величин первой группы, η2 - функцией от величин второй группы и т. д., также являются независимыми.
Независимость случайных величин ξ1, ξ2 означает, что их совместное распределение вероятностей таково, что
Pξ1ξ2 (x1, x2) = Pξ1(x1) Pξ2(x2)(4.10)
для дискретных ξ1, ξ2, и
pξ1ξ2 (x1, x2) = pξ1(x1)* pξ2(x2)(4.10)
для непрерывно распределенных величин ξ1, ξ2, с соответствующими плотностями распределения pξ1ξ2 (x1, x2) и pξ1.(x1), pξ2(x2).
Пример.(Равномерное распределение.) Предположим, что на отрезок [а, b] наугад бросается точка ξ. Условия опыта таковы, что точка ξ с одинаковой вероятностью попадает в любой промежуток (х', х") на отрезке [а, b]. Таким образом, вероятность попадания точки ξ в промежуток (x', х") пропорциональна длине х" - х' этого промежутка, точнее,
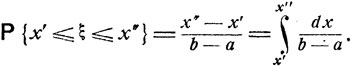
Видно, что случайная величина Е непрерывно распределена с плотностью распределения вероятностей р (х) вида
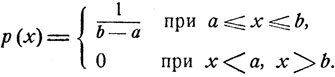
Пример. Предположим, что на отрезок длины L бросаются наугад и независимо друг от друга две точки: ξ1 и ξ2. Какова вероятность того, что расстояние между ними будет не больше l?
Чтобы ответить на этот вопрос, обратимся к следующей модели. Точку ξ1 отложим на отрезке (0, L) оси x1, а точку ξ2 - на отрезке (0, L) оси х2. Искомая вероятность будет совпадать с вероятностью попадания точки ξ = (ξ1, ξ2), наугад бросаемой на квадрат 0≤x1, x2≥L, в область В, ограниченную прямыми x2 = l + x1 и x2 = -1 + x1 (см. рис. 5, где эта область оставлена незаштрихованной). Условия опыта таковы, что случайные величины ξ1 и ξ2 независимы между собой, и каждая из них равномерно распределена на отрезке (0, L), т. е. имеет плотность р(х) вида
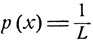
при 0≤x≤L
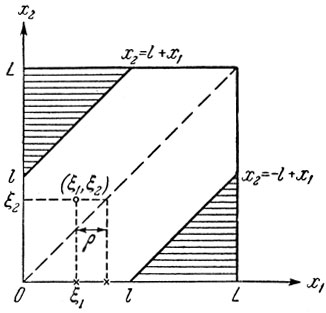
Рис. 5
Для независимых величин ξ1, ξ2 плотность их совместного распределения вероятностей определяется общей формулой (4.11), согласно которой
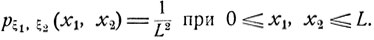
Следовательно, вероятность попадания случайной точки ξ = (ξ1, ξ2) в указанную область В есть
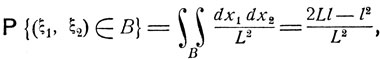
где 2Ll - l2 - площадь области В.
Пример. Предположим, что на плоскость, разлинованную параллельными прямыми, отстоящими друг от друга на расстоянии L, наугад бросается "игла" - отрезок длины l, l≤L Какова вероятность того, что брошенный отрезок пересечет одну из имеющихся линий?
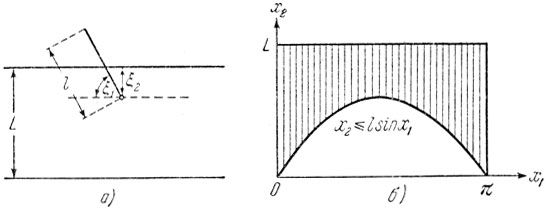
Рис. 6
Обозначим ξ1 угол наклона отрезка к направлению линий, ξ2 - расстояние его нижнего конца до ближайшей сверху линии (рис. 6, а). Условия опыта таковы, что случайная величина ξ1 равномерно распределена на отрезке [0, π], а случайная величина ξ2 - на отрезке [0, L]. Будем считать, что величины ξ1 и ξ2 независимы между собой. Если это так, то плотность их совместного распределения вероятностей есть
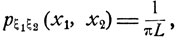
0≤x1≤π, 0≤x2≤L.
Событие "отрезок пересекает одну из линий" наступает тогда и только тогда, когда
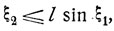
т. е. когда соответствующая точка ξ = (ξ1, ξ2) попадает в область В прямоугольника 0≤x1≤π, 0≤x2≤L, ограниченную сверху кривой x2 = l sin x1 (рис. 6, б). Согласно общей формуле (4.9)
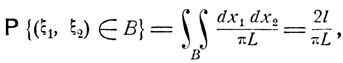
где 2l - площадь указанной области В.
Отметим, что предположение о независимости величин ξ1 и ξ2 которое приводит к данному ответу, может быть проверено практически. Именно, при многократном бросании "иглы" на разлинованную плоскость, частота события A - "отрезок пересекает одну из линий" - должна быть приблизительно равной найденному выше выражению 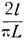 С другой стороны, если верно указанное предположение, то при большом числе испытаний n, исходя из равенства
С другой стороны, если верно указанное предположение, то при большом числе испытаний n, исходя из равенства 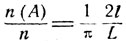 (где
(где 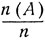 - частота события A) можно с большой точностью определить число π = 3,14 ...
- частота события A) можно с большой точностью определить число π = 3,14 ...
Пример. Пусть ξ1 и ξ2 - независимые между собой величины с соответствующими плотностями распределения pξ1 (ξ1) и рξ(ξ2). Найдем распределение вероятностей случайной величины
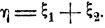
Плотность совместного распределения величин ξ1 и ξ2 равна произведению pξ1 (ξ1) * рξ(ξ2), так что, согласно общей формуле (4.9),
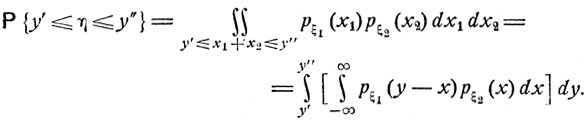
Видно, что случайная величина η имеет плотность распределения вероятностей вида
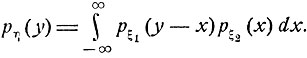
Приведенное выражение называется сверткой или композицией функций pξ1 и рξ.
Если, например, ξ1 и ξ2 равномерно распределены на отрезке [0, 1], так что их общая плотность распределения есть
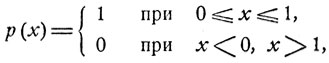
то
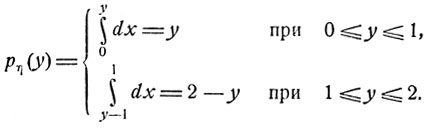
График плотности pη (y) имеет вид треугольника (рис. 7).
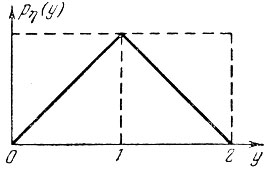
Рис. 7
3. Рассмотрим дискретную случайную величину ξ. Говорят, что ξ имеет математическое ожидание, если

математическим ожиданием (или средним значением) называется выражение
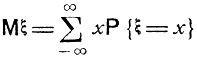
(суммирование идет по конечному или счетному числу значений х, -∞<x<∞, которые может принимать дискретная величина ξ).
Если задано распределение вероятностей случайной величины ξ, то математическое ожидание случайной величины вида η = φ(ξ) (φ = φ(x) - некоторая функция от х) может быть подсчитано по следующей формуле:
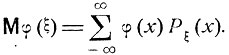
В самом деле, дискретная величина η = φ(ξ) может принимать лишь значения y = φ(ξ), где х пробегает возможные значения дискретной величины ξ, причем
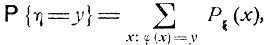
и легко видеть, что
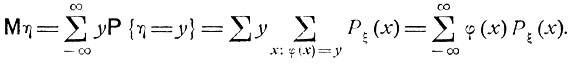
Аналогично, если задано совместное распределение вероятностей случайных величин ξ1 и ξ2, то математическое ожидание Mφ(ξ1, ξ2) случайной величины φ(ξ1, ξ2) являющейся функцией от величин ξ1 и ξ2, задается формулой
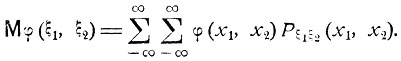
Как видно из самого определения, математическое ожидание обладает следующими свойствами:
M1 = 1;
для любой постоянной c
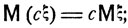
для любых величин ξ1 и ξ2, имеющих математические ожидания Mξ1 и Мξ2,
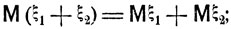
(4.15)
если ξ≥ 0, то Мξ≥ 0; если ξ1≤ξ2, то
Мξ1≤Мξ2;(4.16)
если случайные величины ξ1 и ξ2 независимы, то
M(ξ1ξ2) = Mξ1Mξ2(4.17)
Указанные соотношения (4.15) - (4.17) вытекают из формулы (4.14). Скажем, для независимых ξ1 и ξ2, положив φ(ξ1, ξ2) = ξ1ξ2, имеем:
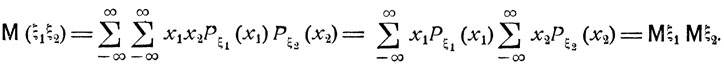
Математическое ожидание определяется и для непрерывно распределенных случайных величин. Именно, всякая случайная величина может быть сколь угодно точно аппроксимирована дискретными величинами. Например, если разбить действительную прямую -∞<x<∞ точками xkn, -∞<k<∞ так, чтобы
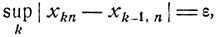
и определить дискретные случайные величины Бξn как
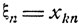
при
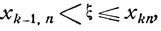
то, очевидно,
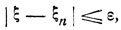
где ε>0 можно выбрать сколь угодно малым. Если взять последовательность величин ξn такого типа (n = 1, 2, ...), для которых
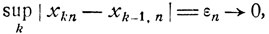
то
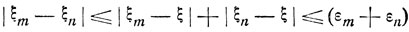
и, согласно неравенству (4.16),
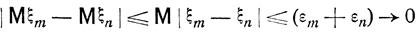
при m, n→∞. Следовательно, существует предел
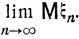
Для непрерывно распределенной случайной величины ξ такой предел и называется математическим ожиданием (или средним значением):
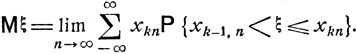
Если задана плотность распределения вероятностей рξ (х), то, выбирая в качестве хkn точки непрерывности функции рξ (х), получим
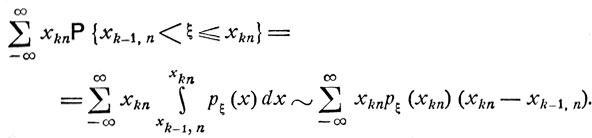
Легко видеть, что
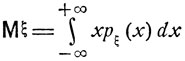
(4.18)
(ср. с формулой (4.13) при φ(x) ≡ x).
Можно доказать*, что так определяемое математическое ожидание обладает всеми установленными ранее свойствами. Аналогично (4.13) и (4.14), математическое ожидание случайной величины вида η = φ(ξ) или η = φ(ξ1, ξ2) может быть подсчитано по следующим формулам:
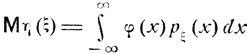
(4.19)
или
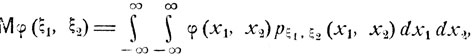
(4.20)
где pξ1, ξ2 (x1, х2) - плотность совместного распределения вероятностей соответствующих случайных величин ξ1, ξ2.
* (См., например, Б. В. Гнеденко, Курс теории вероятностей, изд. 4-е, М., 1965.)
Пример. Пусть ξ - случайная величина, равномерно распределенная на отрезке [а, b], т. е. имеющая плотность распределения вида
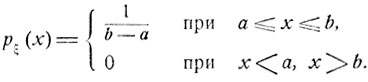
Тогда ее математическое ожидание есть
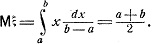
Рассмотрим комплексную случайную величину η = η1 + iη2 (η1 и η2 - действительные и мнимые части величины η). Математическое ожидание Mη определяется как
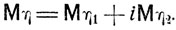
Пусть ξ (или ξ1, ξ2) - действительные случайные величины и η = φ(ξ) (или η = φ(ξ1, ξ2)) является комплекснозначноп функцией от ξ (или ξ1, ξ2). Легко видеть, что, так же как и для действительных величин, имеют место формулы (4.13), (4.19) (или (4.14), (4.20)). Для комплексных величин остаются в силе и другие свойства математических ожиданий. В частности, если случайные величины ξ1 и ξ2независимы, то имеет место формула, обобщающая (4.17):
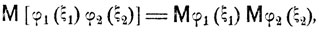
где φ1(ξ1) и φ2(ξ2) - некоторые комплекснозначные функции от ξ1 и ξ2.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'