
§ 3. Связь различных событий. Условные вероятности. Независимые события. Количество информации
1. При анализе того или иного явления перед наблюдателем часто возникает вопрос о том, как влияет на возможность осуществления некоторого события А наступление некоторого другого события В. Простейшим примером связи событий А и В может служить следующее: наступление В ведет к обязательному осуществлению события А или, наоборот, наступление В исключает возможность осуществления события А. В теории вероятностей характеристикой связи событий А и В служит так называемая условная вероятность Р (А|В) события А при условии В, определяемая как
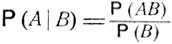
(3.0)
(предполагается, что вероятность события В является положительной).
Величина Р (А|В) может рассматриваться как вероятность осуществления события А при условии наступления события В. Поясним это на примере опыта с конечным числом равновероятных элементарных исходов ω. Пусть N - число всех элементарных исходов, N (B) - число тех из них, которые приводят к наступлению события В, а N (АВ) - число тех элементарных исходов, которые приводят к осуществлению и события A, и события В. В этом случае вероятности событий В и АВ суть 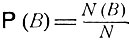 и
и 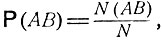 так что условная вероятность Р (А|В) выражается следующей формулой:
так что условная вероятность Р (А|В) выражается следующей формулой:
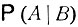
(3.1)
Здесь N (B) - число всех элементарных исходов со, возможных при условии наступления события В, а N (АВ) - число тех из них, которые приводят к осуществлению события А. В соответствии с общей формулой (1.0) равенство (3.1) определяет вероятность события А в новых условиях, которые возникают при наступлении события В.
Условные вероятности обладают всеми свойствами, присущими обычным вероятностям. Именно,
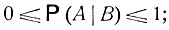
если наступление события В исключает возможность осуществления А (АВ = ∅), то
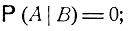
если событие В ведет к обязательному осуществлению события 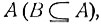 то
то
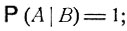
если событие А есть объединение непересекающихся событий 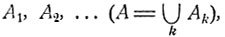 то
то
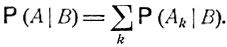
Действительно, если АВ = ∅, т. е. события А и В являются непересекающимися, то P (AB) = 0, откуда и 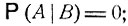 если
если 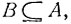 то AB = B и Р (АВ) = Р (В), что равносильно равенству Р (А|В) = 1; если событие А есть объединение непересекающихся событий А1, А2, ..., то произведение АВ является объединением непересекающихся событий A1B, A2B, ... и, согласно общей формуле (2.0),
то AB = B и Р (АВ) = Р (В), что равносильно равенству Р (А|В) = 1; если событие А есть объединение непересекающихся событий А1, А2, ..., то произведение АВ является объединением непересекающихся событий A1B, A2B, ... и, согласно общей формуле (2.0),
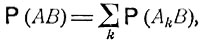
откуда и вытекает указанный выше закон сложения условных вероятностей.
При нахождении вероятности того или иного события A, бывает удобным сначала считать осуществившимся подходящим образом выбранное событие В и определить условную вероятность Р (A|В) как вероятность события A в новых условиях, когда событие В является достоверным. Если имеется некоторая полная система несовместных событий B = B1, B2, ..., т. е. таких, что хотя бы одно из них обязательно осуществится, то вероятность Р (A) события A выражается через соответствующие условные вероятности Р (A|В) при помощи следующей формулы:
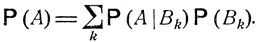
Это соотношение называется формулой полной вероятности. Оно вытекает из закона сложения вероятностей. Действительно, объединение событий В1, В2, ... по условию является достоверным событием: 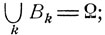 следовательно,
следовательно, 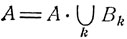 и
и
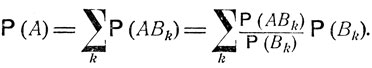
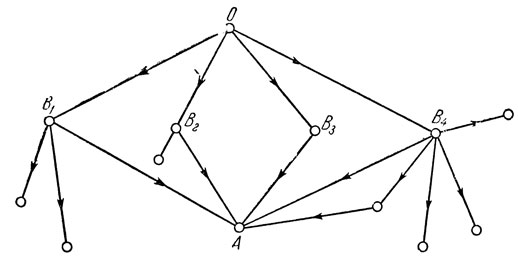
Рис. 3
Пример. Представьте себе странника, идущего из некоторого пункта О и на разветвлении дорог выбирающего наугад один из возможных путей. Схема дорог изображена на рис. 3. На этом рисунке указан также некоторый пункт А и ведущие в него пути. Какова вероятность того, что странник попадет в этот пункт? Как показано на рисунке, его путь обязательно проходит через один из промежуточных пунктов В1, В2, В3, В4. Обозначим через Bk событие, состоящее в том, что при своем движении он попадает в пункт Вk. События В1, В2, В3, В4 образуют полную систему. Очевидно, эти события равновероятны, так как по условию странник выбирает один из путей OВ1, OВ2, OВ3, OВ4 совершенно наугад. Таким образом, Р (Bk) = 1/4. При условии, что странник попадет в В1, он может прийти в A, лишь выбрав одно из трех равновероятных направлений движения из пункта В1, так что условная вероятность прийти в A при условии В1 равна 1/3. Если обозначить через А событие, состоящее в том, что странник приходит в пункт A, то, как было сказано, 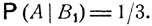 Совершенно аналогично
Совершенно аналогично
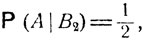
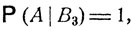
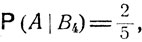
и по формуле полной вероятности
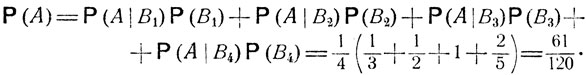
Задача о наилучшем выборе. Предположим, что имеется некоторая совокупность из m предметов, сравнивая которые, наблюдатель может сказать, который лучше или хуже, а задача состоит в том, чтобы выбрать предмет как можно лучше. Предположим, что эта задача осложняется следующим обстоятельством: осмотрев и отвергнув некоторый предмет, нельзя к нему снова возвращаться. Тогда, в частности, можно случайно отвергнуть абсолютно наилучший предмет в надежде найти еще более лучший при дальнейшем осмотре (представьте себе, например, разборчивую невесту, которая либо принимает предложение сватающегося жениха - и тогда на этом выбор заканчивается, либо отвергает его - и тогда он безвозвратно потерян для невесты).
Рассмотрим одно естественное правило выбора: не останавливаться на том предмете, который хуже какого-нибудь уже ранее осмотренного предмета. Будем считать, что наблюдатель руководствуется этим правилом, так что при последовательном осмотре имеющихся предметов он может сразу выбрать первый из них (и на этом процесс выбора закончится); если он этого не сделал, то он продолжает осмотр до тех пор, пока на каком-то шаге не окажется предмет, который будет лучше всех осмотренных ранее; наблюдатель может выбрать этот наилучший среди осмотренных предметов (и на этом процесс выбора закончится), а может продолжить осмотр в надежде найти еще лучше, и т. д.
Конечно, при этом не исключено, что на самом деле будет отвергнут абсолютно наилучший предмет, и тогда вообще ничего не будет выбрано. Но если число имеющихся предметов велико, то едва ли кто-нибудь согласится взять первый попавшийся предмет, не испытав счастья найти что-нибудь получше.
Предположим, что, следуя описанному правилу, наблюдатель сделал выбор, остановившись на k-м осмотренном предмете, т. е. последний из k осмотренных предметов оказался лучше всех предшествующих и на него-то и пал выбор. Какова вероятность того, что этот выбранный предмет является наилучшим среди всей совокупности как осмотренных, так и еще не осмотренных предметов?
Обозначим В событие, состоящее в том, что среди k осмотренных предметов последний оказался наилучшим. Наблюдателю известно о том, что событие В произошло. Обозначим A событие, состоящее в том, что k-й по счету предмет является 8 наилучшим среди всех имеющихся предметов. Вопрос касается условной вероятности Р (A|В) события A при условии наступления события В. Эта условная вероятность Р (А|В) находится по формуле (3.0), так что для ответа на поставленный вопрос нужно найти вероятности событий В и АВ. Очевидно, событие А содержится в В и пересечение АВ совпадает с самим событием A. Описанные условия выбора таковы, что следует считать все возможные расположения предметов равновероятными. Вероятность события В совпадает с вероятностью того, что при случайной перестановке k отличимых друг от друга элементов (они отличаются по качеству) на фиксированном k-м месте окажется наилучший из этих k элементов. Такая вероятность равна (k - 1)!/k! где k! - число перестановок из k, (k-1)! - число перестановок из k-1 элементов, совместимых с тем условием, что на k-м месте зафиксирован наилучший элемент. Итак,
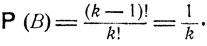
Совершенно аналогично находится вероятность события A, которая совпадает с вероятностью того, что при случайной перестановке m отличимых друг от друга элементов на фиксированном k-м месте окажется вполне определенный элемент - наилучший предмет из всей имеющейся совокупности m предметов. Таким образом,
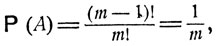
и искомая условная вероятность 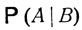 есть
есть
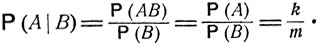
Задача о разорении игрока. Рассмотрим игру в так называемую "орлянку", когда игрок выбирает "герб" или "решетку", после чего бросается монета. Если выпадает та сторона монеты, которая была названа игроком, то он выигрывает, получая, скажем 1 руб.; в противном случае он столько же проигрывает. Предположим, что начальный капитал игрока составляет х рублей и игрок ставит себе целью довести его до некоторой суммы в а рублей. Игра продолжается до тех пор, пока либо игрок наберет заранее определенную сумму а, либо разорится, проиграв весь имеющийся у него капитал. Какова вероятность того, что в конце концов игрок разорится, так и не набрав желаемую сумму а рублей?
Ясно, что эта вероятность зависит от начального капитала х и конечной суммы а. Обозначим p (х) вероятность того, что, имея х рублей, игрок все-таки разорится. Тогда вероятность разорения при условии выигрыша на первом шаге в наших обозначениях будет р (х + 1), так как после выигрыша капитал игрока станет равным х + 1. Аналогично вероятность разорения при условии проигрыша на первом шаге равна р (х - 1), так как после проигрыша капитал игрока станет равным х - 1.
Обозначим В1 событие, заключающееся в том, что игрок выиграл на первом шаге, B2 - событие, заключающееся в том, что он проиграл. Условные вероятности разорения - события А - в принятых нами обозначениях суть
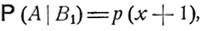
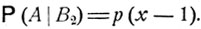
События В1 и В2 образуют полную систему, так как на первом шаге игрок либо выигрывает, либо проигрывает. Очевидно,
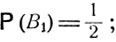
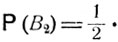
Формула полной вероятности дает следующее уравнение для вероятностей р(х):
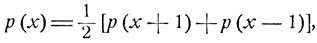
1≤x≤a-1,
причем
p(0) = 1, р(а) = 0.
Решением этого уравнения является линейная функция
р(х) = C1 + C2x,
коэффициенты которой должны быть определены из указанных граничных условий. Имеем
C1 = 1, C1 + C2x = 0,
откуда получаем окончательное выражение для искомой вероятности разорения р (х) при начальном капитале х:
р(х) = 1 - x/a, 0≤х≤а.
2. Рассмотрим два независимых друг от друга опыта. Понятно, что это значит: никакой исход одного опыта никак не влияет на исходы другого; Рассмотрим какие-либо событие А1 (связанное только с первым опытом) и событие A2 (связанное только со вторым опытом). Наступление события А1 никак не влияет на возможность осуществления A2 и, наоборот, событие A2 никак не влияет на А1. В этом смысле можно сказать, что события А1 и A2 независимы друг от друга. Какова вероятность совместного осуществления этих событий?
Для того чтобы ответить на этот вопрос, обратимся к эмпирически установленному факту, согласно которому частота какого-либо события в большой серии независимых испытаний приблизительно совпадает с его вероятностью (см. по этому поводу п. 1 § 1). Мысленно представим себе, что имеется большая серия независимых испытаний, в каждом из которых проводятся оба рассматриваемых опыта. Если число всех испытаний равно n, а n (A1А2) - число тех испытаний, которые привели к одновременному наступлению событий А1 и A2, то искомая вероятность Р (А1А2) может быть вычислена приближенно как
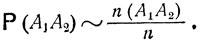
Рассмотрим теперь только те испытания, при которых осуществляется событие A2. Пусть число таких испытаний есть n (A2). Имеет место приближенное равенство
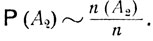
При достаточно большом n велико и число n(A2) тех испытаний, в которых осуществляется событие A2. Но событие A2 связано только со вторым опытом, который проводится совершенно независимо от первого опыта и связанного с ним события A1. В указанной серии из n(A2) испытаний, завершающихся наступлением события A2, будем рассматривать результаты первого опыта. Число тех испытаний, которые приводят к наступлению события A1, равно указанному выше числу n(A1A2), так что
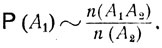
Полученные соотношения дают возможность выразить вероятность совместного осуществления независимых событий А1 и A2 через вероятности Р (А1) и Р (A2) этих событий:
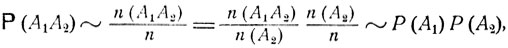
или (после перехода к точному равенству)
Р (А1А2) = Р (А1) Р (А2). (3.3)
Отвлекаясь от физических условий того или иного опыта, в теории вероятностей называют независимыми всякие два события A1 и A2, для которых имеет место равенство (3.3).
Это определение независимости событий хорошо согласуется с введенным ранее понятием условной вероятности. Именно, событие А1 является независимым от события A2 тогда и только тогда, когда наступление события A2 никак не влияет на вероятность наступления события А1, точнее, когда условная вероятность Р (А1|A2) события А1 при условии наступления события A2 точно такая же, как и безусловная вероятность этого события:
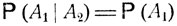
(события А1 и A2 здесь можно поменять местами). В самом деле, соотношение
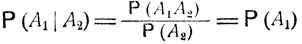
имеет место тогда и только тогда, когда выполнено равенство (3.3).
Пример 1. Рассмотрим следующий опыт. Из карточной колоды, содержащей 36 карт, наугад вытягивается одна карта. Пусть событие А1 состоит в том, что это "пика", а событие A2 - что это "дама". Являются ли независимыми эти события?
Едва ли здесь легко дать ответ, основываясь лишь на физической интуиции. Элементарные же подсчеты показывают, что вероятность Р (А1) вытащить одну из имеющихся в колоде 9 "пиковых" карт есть 9/36 = 1/4, вероятность Р (A2) вытащить одну из имеющихся четырех "дам" есть 4/36 = 1/9, вероятность Р (A1А2) вытянуть "даму пик" есть 1/36, и видно, что Р (A1A2) = Р (А1) Р (А2). Таким образом, события A1 и A2
являются независимыми.
Пример 2. Бросаются две игральные кости. Пусть событие А1 состоит в том, что нечетная грань выпадает на первой кости, A2 - нечетная грань выпадает на второй кости и A3 - сумма выпавших очков является нечетной. Ясно, что исход бросания одной кости никак не влияет на исход бросания другой, так что события А1 и A2 независимы друг от друга:
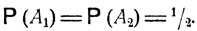
При одном из условий A2 или А1 событие A3 наступает тогда и только тогда, когда на первой или второй кости соответственно выпадает четное число очков, и легко видеть, что
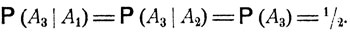
Таким образом, А1 и A2, A2 и A3, A3 и A1 представляют собой пары независимых друг от друга событий. В то же время при условии одновременного наступления событий А1 и A2 событие A3 просто невозможно, так что нельзя считать событие A3 независимым от совокупности событий А1 и A2.
События Ak, k = 1, 2, ..., называются независимыми, если для любой группы событий Аi1, ..., Ain (1i1<...<in≤k) вероятность их пересечения равна произведению вероятностей отдельных событий:
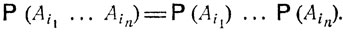
(3.4)
Предположим, что рассматриваются различные группы независимых событий А1, A2, ..., скажем,
(Аi1, Ai2, ...), (Аj1, Aj2, ...), ...
(каждое из событий входит лишь в одну из рассматриваемых групп); тогда события В1, В2, ..., где В1 является какой-либо комбинацией событий из первой группы, В2 - комбинацией событий из второй группы и т. д., также являются независимыми.
3. Как можно количественно оценить ту или иную информацию?
Если речь идет об информации, которая заключена в том или ином письменном тексте, то при самом грубом подходе предположительно можно измерить ее длиной самого текста. При этом, конечно, нужно выбрать какой-то подходящий способ записи, какое-то подходящее правило кодирования информации.
Пусть имеется N каких-либо объектов. Для их обозначения воспользуемся так называемым двоичным кодом, сопоставив каждому объекту соответствующую кодовую комбинацию вида (а1, ..., ad), где символы ak принимают одно из двух возможных значений 0 или 1 и длина d всех кодовых комбинаций одна и та же. Всего имеется 2d различных кодовых комбинаций такого типа. Следовательно, чтобы различать N объектов, нужно выбрать длину d кодовой комбинации так, чтобы N≤2d. Наименьшее d, при котором это возможно, есть натуральное число, удовлетворяющее соотношению
0≤d-log2N<1.
Видно, что величина
I = log2 N
характеризует длину наиболее экономных кодовых комбинаций, при помощи которых можно описать N различных объектов.
Предположим, что рассматривается некоторый опыт, результатом которого может быть одно из N, равновероятных и непересекающихся между собой событий А1, ..., AN. Как количественно оценить ту информацию, которая заключена в сообщении об исходе Ai такого опыта?
В теории вероятностей эта информация оценивается указанной выше величиной
I = log2 N.
Пусть рассматриваемые события А1, ..., AN имеют различные вероятности
р1 = Р (А1), ..., pN = р(АN).
Ясно, что сообщение о наступлении маловероятного события несет в себе больше информации, чем сообщение о наступлении события, которое ожидается с большой вероятностью. В частности, сообщение о наступлении достоверного события фактически не несет никакой информации (и без этого сообщения известно, что достоверное событие обязательно произойдет).
Предположим, что проводится серия независимых и одинаковых испытаний, в каждом из которых наступает одно из рассматриваемых событий А1, ..., AN. Сообщение об исходе n испытаний можно условно записать в виде последовательности (Ai1, Ai2, ..., Ain), где Aik - то событие из A1, ..., AN, которое имело место при k-м испытании. Согласно тому, что частота 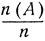 события А в большой серии испытаний практически совпадает с его вероятностью Р (A), в сообщении (Ai1, Ai2, ..., Ain) событие А1 приблизительно встречается n1˜p1n раз, событие A2 приблизительно встречается n2˜p2n раз и т. д., событие AN встречается приблизительно nN˜pNn раз. Только такие исходы и рассматриваются ниже.
события А в большой серии испытаний практически совпадает с его вероятностью Р (A), в сообщении (Ai1, Ai2, ..., Ain) событие А1 приблизительно встречается n1˜p1n раз, событие A2 приблизительно встречается n2˜p2n раз и т. д., событие AN встречается приблизительно nN˜pNn раз. Только такие исходы и рассматриваются ниже.
Число всех исходов, в которых событие А1 наступает ровно n1 раз, событие A2 ровно n2 раз и т. д., событие AN наступает ровно nN раз (n1 + n2 + ... + nN = n) по формуле (1.7) есть
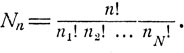
Вероятность каждого из описанных исходов есть
P (Ai1) P (Ai2) ... P (Ain) = p1n1p2n2 ... pNnN.
Используя формулу Стирлинга при n→∞ и n1˜p1n, n2˜p2n, ..., nN˜pNn имеем
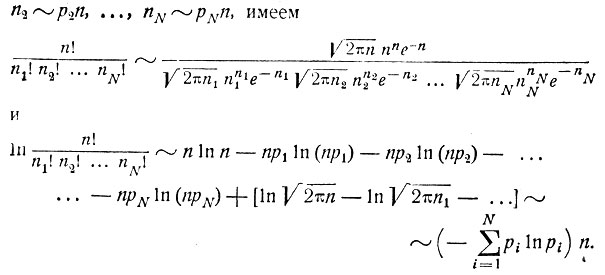
Итак, рассматриваемые исходы (Ai1, Ai2, ..., AiN) приблизительно равновероятны, а число их Nn таково, что
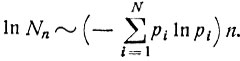
Если для обозначения этих исходов (Ai1, Ai2, ..., AiN) в серии из n испытаний воспользоваться двоичным кодом, то длина наиболее экономной кодовой комбинации будет приблизительно 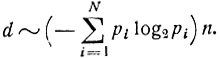 В среднем на каждое из n испытаний это составит
В среднем на каждое из n испытаний это составит
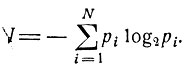
В теории вероятностей определяемая формулой (3.5) величина I принята за количество информации, которую в среднем несет сообщение о наступлении одного из событий А1, ..., AN в каждом отдельном опыте. Для равновероятных событий эта величина есть I = log2 N.
Было получено экспериментальное подтверждение формулы (3.5) для количества информации. Например, в ряде опытов обнаружено, что передача информации в живом организме происходит таким образом, что затрачиваемое на это время пропорционально количеству информации, вычисляемому по формуле (3.5).
Примером подобного рода может служить один из простейших опытов по определению среднего времени психических реакций. Опыт заключается в том, что перед испытуемым человеком зажигается одна из N лампочек, которую он должен указать. Проводится большая серия испытаний, в которых каждая лампочка зажигается с определенной вероятностью рi. Оказывается*, среднее время, необходимое для правильного ответа испытуемого, пропорционально именно величине 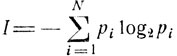 (а не числу лампочек N, как можно было бы подумать).
(а не числу лампочек N, как можно было бы подумать).
* (См. А. М. Яглом и И. М. Яглом, Вероятность и информация, изд. 2-е, М., 1960.)
Вообще количество информации о событиях А1, A2, ..., которое несет сообщение о наступлении события из В1, B2, ..., определяется формулой
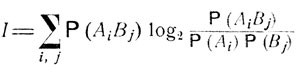
(3.6)
(здесь А1, A2, ... и В1, В2, ... - некоторые полные системы непересекающихся событий).
Пример. Предположим, что в некотором пункте за весенне-летний сезон примерно в одном из пяти случаев бывает дождь, в остальных случаях - ясная погода. Допустим, что накануне дается прогноз погоды. Естественно, этот прогноз может оказаться ошибочным. Предположим, что прогноз дождя бывает ошибочным приблизительно в половине всех случаев (правильно предсказать маловероятное событие - дождь - весьма трудно), а прогноз ясной погоды действует точнее и оказывается ошибочным лишь в одном случае из десяти. Каково количество информации, которое в среднем несет в себе прогноз погоды?
Введем следующие обозначения: А1 - дождь, А2 - ясная погода, В1 - прогноз дождя, B2 - прогноз ясной погоды. Следует положить
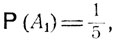
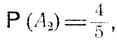
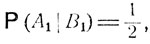
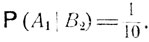
Из формулы полной вероятности
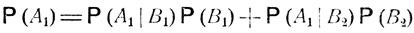
находим, что
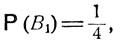
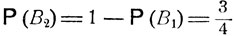
и
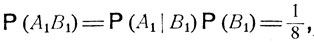
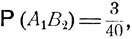
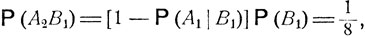
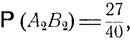
откуда, согласно формуле (3.6),
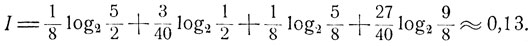
Насколько больше информации несет абсолютно безошибочный прогноз?
В случае безошибочного прогноза следует положить В1 = А1, В2 = А2, и тогда
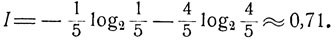
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'