
§ 2. Комбинации событий. Пространство элементарных событий. Закон сложения вероятностей
1. Предположим, что в результате рассматриваемого опыта или явления происходит один из взаимно исключающих друг друга исходов, которые будем обозначать греческой буквой ω и называть элементарными событиями или элементарными исходами. Совокупность всех элементарных исходов ω обозначим Ω и будем называть пространством элементарных событий.
Будем говорить, что событие А связано с рассматриваемым опытом (или с элементарными исходами ω), если по каждому элементарному исходу ω можно точно судить о том, осуществляется или нет данное событие A. Обозначим тем же символом А совокупность (иначе, множество) всех элементарных исходов ω, в результате которых наступает событие А. Очевидно, событие А происходит тогда и только тогда, когда наступает один из элементарных исходов ω, входящий в указанную совокупность А, так что, вместо того чтобы говорить об исходном событии А, можно говорить лишь о событии "наступает элементарный исход ω, входящий в совокупность A". В дальнейшем мы не будем делать различия между связанными с рассматриваемым опытом событиями и соответствующими множествами элементарных исходов, фактически подразумевая, что каждый раз речь идет о событии типа: "наступает элементарный исход ω, входящий в множество A". При такой интерпретации события - это определенные множества элементарных исходов ω соответствующего пространства элементарных событий Ω. При этом достоверное событие A, наступающее в результате любого исхода рассматриваемого опыта, формально отождествляется со всем пространством Ω, а невозможное событие (обозначаемое символом ∅) трактуется как пустое множество, не содержащее ни одного из элементарных исходов ω.
События А1 и A2 называются равными (А1 = А2), если осуществление события A1 влечет за собой осуществлению события A2, и наоборот, осуществление A2 влечет за собой осуществление A1.
Пример. При бросании двух игральных костей равными оказываются события А1 - "выпадает четная сумма очков" - и A2 - "на каждой грани выпадают очки одной и той же четности". Аналогичные события в другом опыте, когда бросаются не две, а три игральные кости, уже не будут равными.
События А1 и A2 называются несовместными или непересекающимися, если наступление одного из этих событий исключает, возможность наступления другого, иначе говоря, А1 и A2 не могут произойти одновременно.
Объединением или суммой событий А1 и A2 называется событие A, которое означает осуществление хотя бы одного из событий А1 A2: 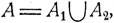 где ∪ - специальный символ объединения. Аналогично определяется объединение событий А1, A2, ..., обозначаемое как
где ∪ - специальный символ объединения. Аналогично определяется объединение событий А1, A2, ..., обозначаемое как 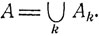
Пересечением или произведением событий А1 и A2 называется событие A, которое означает осуществление и события А1, и события 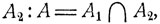 где ∪ - специальный символ пересечения. Аналогично определяется произведение событий А1А2 ..., обозначаемое как
где ∪ - специальный символ пересечения. Аналогично определяется произведение событий А1А2 ..., обозначаемое как 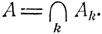
Разностью событий А1 и A2 называется событие A, которое означает, что происходит событие А1, но не происходит событие 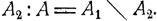 Дополнительным к событию A называется событие
Дополнительным к событию A называется событие 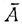 , которое означает, что событие A не происходит:
, которое означает, что событие A не происходит: 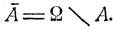
Пример. Рассмотрим опыт с бросанием двух игральных костей. Событие A - "выпадает четная сумма очков" - есть объединение непересекающихся событий А1 - "на каждой грани выпадает четное число очков" - и A2 - "на каждой грани выпадает нечетное число очков". При этом A1 = А \ A2 и A2 = A \ A1. Дополнительным к событию А является событие 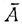 - "выпадает нечетная сумма очков", дополнительным к А1 является событие
- "выпадает нечетная сумма очков", дополнительным к А1 является событие 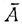 1 - "хотя бы на одной грани выпадает нечетное число очков" - и дополнительным к событию A2 является событие
1 - "хотя бы на одной грани выпадает нечетное число очков" - и дополнительным к событию A2 является событие 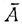 2 - "хотя бы на одной грани выпадает четное число очков". При этом
2 - "хотя бы на одной грани выпадает четное число очков". При этом 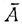 1 \
1 \ 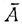 =
= 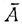 1*A = A2 и
1*A = A2 и 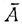 2 \
2 \ 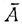 =
= 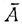 2*А = А1.
2*А = А1.
Понятия объединения, пересечения и т. д. приобретают большую наглядность, если, согласно предложенному выше, интерпретировать события как некоторые совокупности элементарных исходов ω: А1∪A2 есть объединение совокупностей А1 и A2; A1∩A2 - пересечение (общая часть) этих совокупностей; 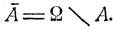 - совокупность элементарных исходов, дополняющая множество A до всего пространства Ω; соотношение "событие А1 влечет за собой наступление события A2" (иначе, "событие А1 содержится в A2") означает, что множество А1 содержится во множестве A2, что обозначается как
- совокупность элементарных исходов, дополняющая множество A до всего пространства Ω; соотношение "событие А1 влечет за собой наступление события A2" (иначе, "событие А1 содержится в A2") означает, что множество А1 содержится во множестве A2, что обозначается как 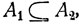 где
где 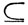 - специальный символ включения, и т. д.
- специальный символ включения, и т. д.
Чтобы представить себе, в каком отношении между собой находятся те или иные события, бывает удобным условно считать пространство элементарных событий Ω некоторой областью на плоскости, элементарные исходы ω - точками плоскости, лежащими внутри Ω; при этом события - определенные совокупности точек ω - удобно изображать в виде некоторых фигур. На рис. 2 показаны различные соотношения между событиями A1 и A2, которые изображаются в виде фигур на плоскости, лежащих внутри прямоугольника Ω, условно изображающего пространство элементарных событий.
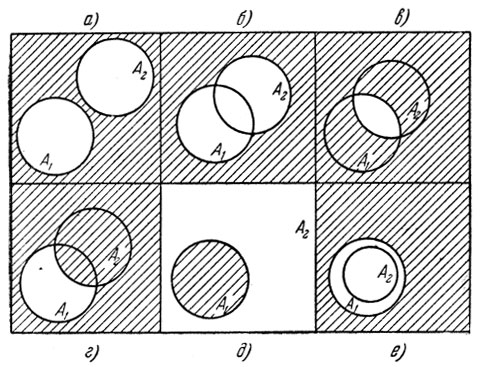
Рис. 2. а) А1 и A2 - несовместные (непересекающиеся) события, б) Незаштрихованная фигура изображает объединение А1∩A2. в) Незаштрихованная фигура изображает пересечение А1∪А2. г) Незаштрихованная фигура изображает разность A1\A2. д) Событие A1 является дополнительным к событию A2. е) Событие A2 содержится в A1
Используя наглядные свойства фигур на плоскости, можно легко увидеть, что имеют место следующие общие связи между различными соотношениями событий. Именно, если 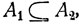 то
то  если
если 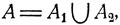 то
то 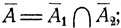 если
если 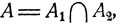 то
то 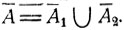 Вообще, если справедливо некоторое соотношение между какими-то событиями, то будет справедливо и соотношение, получаемое из исходного переходом к дополнительным событиям и заменой знаков объединения ∩, пересечения ∪ и включения
Вообще, если справедливо некоторое соотношение между какими-то событиями, то будет справедливо и соотношение, получаемое из исходного переходом к дополнительным событиям и заменой знаков объединения ∩, пересечения ∪ и включения 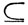 на соответствующие "обратные" знаки ∪, ∩ и
на соответствующие "обратные" знаки ∪, ∩ и 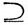 (знаки равенства = остаются неизменными).
(знаки равенства = остаются неизменными).
Пример. Равносильными оказываются следующие соотношения:
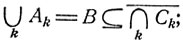
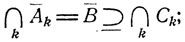
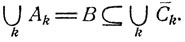
2. Рассмотрим несовместные события A1, A2 и их объединение 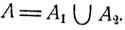 Представим себе, что проводится серия одинаковых и независимых между собой опытов, результатом каждого из которых могут быть указанные события A, А1 или A2. Пусть n - число всех испытаний; n (A), n (А1) и n (A2) - число тех из них, которые привели к наступлению соответствующих событий A, А1 и A2. Если в каком-то опыте произошло событие A, то это значит, что произошло или событие А1 или событие A2 (одновременно А1 и A2 произойти не могут, так как по условию они являются несовместными). Поэтому числа n (A), n (А1) и n (A2) связаны между собой следующим равенством:
Представим себе, что проводится серия одинаковых и независимых между собой опытов, результатом каждого из которых могут быть указанные события A, А1 или A2. Пусть n - число всех испытаний; n (A), n (А1) и n (A2) - число тех из них, которые привели к наступлению соответствующих событий A, А1 и A2. Если в каком-то опыте произошло событие A, то это значит, что произошло или событие А1 или событие A2 (одновременно А1 и A2 произойти не могут, так как по условию они являются несовместными). Поэтому числа n (A), n (А1) и n (A2) связаны между собой следующим равенством:
n (А) = n (А1) + n (А2).
Следовательно, частоты рассматриваемых событий таковы, что
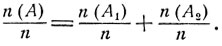
При достаточно большом числе испытаний частоты практически совпадают с соответствующими вероятностями (см. по этому поводу п. 1 § 1), так что вероятности рассматриваемых событий 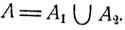 А1 и A2 должны быть связаны между собой следующим равенством:
А1 и A2 должны быть связаны между собой следующим равенством:
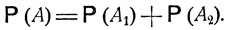
Полученное равенство является выражением так называемого закона сложения вероятностей, согласно которому для любых непересекающихся событий А1, А2, ... вероятность их объединения 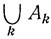 есть
есть
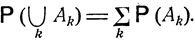
(2.0)
Если соотношения между событиями наглядно описываются соотношениями между изображающими их фигурами на плоскости (см. рис. 2), то свойства вероятностей вполне аналогичны свойствам площадей этих фигур. Именно, вероятность Р (А) события А есть неотрицательное число
0≤P (A)≤1
(причем невозможное событие А = ∅ имеет вероятность 0, а достоверное событие А = Ω имеет вероятность 1). Так же как и для площадей, имеют место закон сложения и все вытекающие из него следствия. В частности, если А1 содержится в A2, то
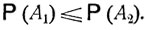
(2.1)
Для любых событий А1 и A2
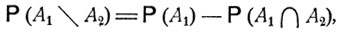
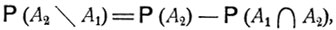
(2.2)
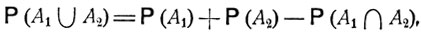
Действительно, каждое из событий А1 и А2 может быть представлено в виде
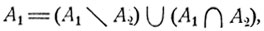
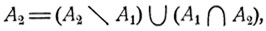
где события 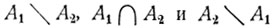 являются непересекающимися, так что, согласно формуле (2.0),
являются непересекающимися, так что, согласно формуле (2.0),
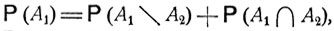
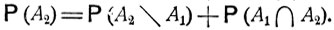
Отсюда видно, что если 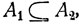 то
то 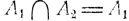 и
и
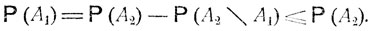
Столь же очевидны и первые два равенства (2.2). Далее, сумма А1∪A2 событий А1 и A2 может быть представлена как сумма непересекающихся событий A1\A2, A2\A1 и 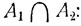
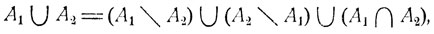
и потому
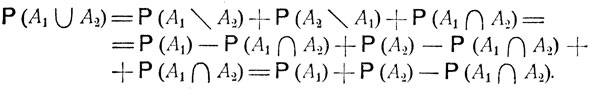
Введем одну формулу для вероятности объединения событий А1, A2, ..., Аn. Положим
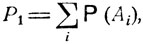
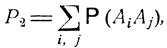
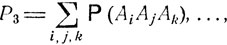
где 1≤i<j<k...≤n, так что каждая группа индексов (i, j, k, ...) при суммировании встречается лишь один раз. Имеет место следующая общая формула для вероятности 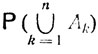 объединения
объединения 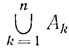 событий А1, ..., Аn:
событий А1, ..., Аn:
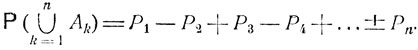
(2.3)
Докажем эту формулу методом индукции. При n = 2 она превращается в уже доказанное равенство (2.2). Предположим, что формула верна для объединения любых n - 1 событий, так что
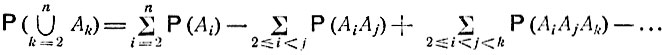
и
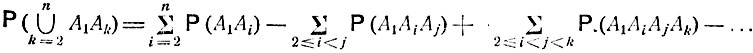
Имеем
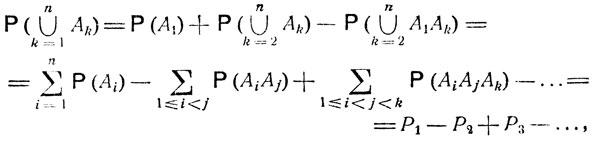
что и требовалось доказать.
Пример. Задача о совпадениях. Представьте себе, что группа студентов имеет одинаковые плащи-дождевики, которые по стечению обстоятельств оказались на одной вешалке; Каждый из студентов выбирает себе плащ наугад, не имея возможности отличить свой плащ от других. Какова вероятность того, что хотя бы один из плащей попадет к своему прежнему владельцу?
Эта вероятность, конечно, зависит от числа студентов. Для удобства перенумеруем все плащи в некотором порядке числами 1, ..., n. Соответствующими номерами снабдим и студентов, так что в наших обозначениях k-й плащ принадлежит k-му студенту. Обозначим Ak событие, состоящее в том, что k-й студент взял именно свой плащ. Тогда событие А - "хотя бы один плащ попадает к своему прежнему владельцу" - является объединением событий A1, ..., Аn: А = 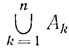 . Каждый k элементарный исход "случайного разбора" плащей можно описать перестановкой чисел (i1, i2, ..., in), где ik означает номер плаща, выбранного k-м студентом. Подсчитаем вероятность пересечения событий Ak1 Ak2 ... Akm. Указанное событие наступает, когда числа ik1, ik2, ..., ikm принимают фиксированные значения: ik1 = k1, ik2 = k2, ..., ikm = km, а остальные номера могут быть расположены в любом порядке. Поэтому
. Каждый k элементарный исход "случайного разбора" плащей можно описать перестановкой чисел (i1, i2, ..., in), где ik означает номер плаща, выбранного k-м студентом. Подсчитаем вероятность пересечения событий Ak1 Ak2 ... Akm. Указанное событие наступает, когда числа ik1, ik2, ..., ikm принимают фиксированные значения: ik1 = k1, ik2 = k2, ..., ikm = km, а остальные номера могут быть расположены в любом порядке. Поэтому
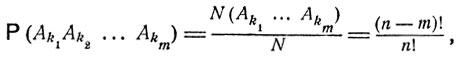
где N (Ak1, ... Akm) = (n - m)! - число всех возможных перестановок из n-m, N = n! - число всех возможных перестановок из n, m - число фиксированных номеров ik1 = k1, ..., ikm = km. Различных событий вида Ak1, Ak2, ..., Akm насчитывается всего
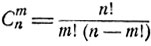
- столько различных групп k1, k2, ..., km можно образовать из совокупности чисел 1, 2, ..., n. Поэтому
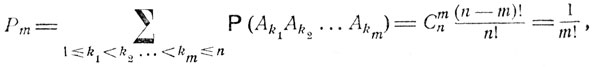
и вероятность объединения событий A1, A2, ..., Аn по формуле (2.3) есть
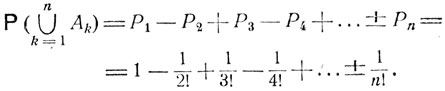
Искомая вероятность Р (А) совпадает с частичной суммой ряда в разложении функции 1 - ех при х = -1:
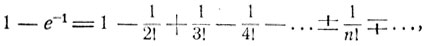
так что для больших n
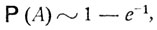
e = 2, 78 ...
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'