§ 1. Опыт с равновероятными исходами. Вероятность и частота. Некоторые комбинаторные формулы. Формула Стирлинга

1. Рассмотрим такой простой опыт, как бросание монеты. Он имеет два взаимно исключающих исхода: выпадение "герба" и выпадение "решетки". Наблюдатель не может проанализировать и учесть все те многочисленные факторы, которые влияют на результат рассматриваемого опыта,- исход бросания монеты является случайным. Какова вероятность выпадения "герба" (или "решетки")? Несомненно, каждый ответит, что эта вероятность равна ¹/₂. Такой ответ интуитивно основывается на том, что рассматриваемые исходы равноправны по отношению к условиям опыта, т. е. эти исходы равновероятны. Но вряд ли кто отдает себе отчет в том, что такое, собственно, есть вероятность, какой смысл вкладывается в это понятие.

Рассмотрим некоторый опыт с конечным числом взаимно исключающих друг друга исходов, которые равноправны по отношению к условиям данного опыта, т. е. равновероятны. Обозначим А некоторое событие, связанное с указанными исходами. ВероятностьР (А) события А можно было бы определить как долю тех исходов, в результате которых это событие осуществляется:

где N - общее число исходов рассматриваемого опыта, N(A) - число тех из них, которые приводят к наступлению события А Например, при бросании монеты имеется 2 взаимно исключающих равновероятных исхода (выпадение "герба" и выпадение "решетки"), и если А - любое из этих событий, то вероятность Р (A) равна ¹/₂, поскольку N(A) = 1. При бросании игральной кости - правильного кубика с занумерованными гранями - имеется 6 взаимно исключающих друг друга и равновероятных исходов (выпадение определенного числа очков от 1 до 6) и, скажем, вероятность Р(Д) события А - "выпадает четное число очков" - равна ¹/₂, поскольку здесь N(A) = 3. При бросании двух игральных костей имеется 36 взаимно исключающих друг друга и равновероятных исходов (выпадение пары чисел (а, b), где а - число очков. на первой кости, b - число очков на второй кости) и, скажем, вероятность Р (А) события А - "на обеих костях выпадает одинаковое число очков" - равна ¹/₆, поскольку событие А наступает в результате любого из 6 исходов, при которых а = b, т. е. N(A) = 6.

Накопленные практикой многочисленные наблюдения выявили одну замечательную закономерность, которая позволяет придать глубокий смысл понятию вероятности как в рассмотренном выше опыте с равновероятными исходами, так и в самом общем случае. Именно, предположим, что рассматриваемый опыт, явление и т. п. могут быть воспроизведены многократно, так что в принципе осуществима целая серия одинаковых и независимых друг от друга испытаний, в каждом из которых по воле случая происходит или не происходит интересующее наблюдателя событие А. Пусть n обозначает число всех опытов в отдельной серии испытаний и n(А) - число тех из них, в которых осуществляется событие А. Отношение 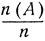называется частотой события А в данной серии испытаний. Оказывается, в различных сериях испытаний соответствующие частоты 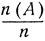при больших n практически совпадают, группируясь около некоторого постоянного значения Р (А), называемого вероятностью события А:

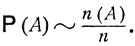
(1.1)

Формально указанное соотношение нужно понимать следующим образом:

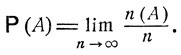
Согласно этой эмпирически установленной закономерности вероятность Р (А) события А характеризует долю тех случаев в большой серии опытов, которые приводят к наступлению этого события. Ниже приведены результаты серий опытов с бросанием монеты, которая в общей сложности бросалась 10 000 раз^*. В приводимой ниже таблице даны числа n (А) - количество опытов в отдельной серии из n = 100 испытаний, которые привели к осуществлению события А (выпадение "герба").

^* (См. В. Феллер, Введение в теорию вероятностей и ее приложения (перев. с англ.), изд. 2-е, М., 1964.)

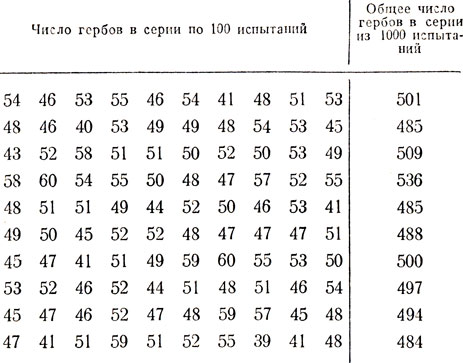
Из таблицы видно, что частоты 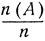выпадения "герба" в каждой из серий по n = 100 испытаний поразительно мало отличаются от вероятности Р (A) = ¹/₂, подсчитанной по формуле (1.0).

Отметим сразу, что, несмотря на внешнюю простоту этой формулы, применение ее при рассмотрении каждого конкретного опыта, явления и т. п. ставит перед наблюдателем дополнительную задачу по выявлению тех равновероятных исходов, с которыми связано то или иное событие А

Пример. Парадокс де Мере^*. Многократно наблюдая игру в кости, француз де Мере подметил, что при одновременном бросании трех игральных костей более часто выпадает комбинация, дающая в сумме 11 очков, чем комбинация, дающая в сумме 12 очков, хотя, с его точки зрения, эти комбинации были равновероятны. Де Мере рассуждал следующим образом: 11 очков можно получить шестью различными способами (6-4-1, 6-3-2, 5-5-1, 5-4-2, 5-3-3, 4-4-3) и столькими же способами можно получить 12 очков (6-5-1, 6-4-2, 6-3-3, 5-5-2, 5-4-3, 4-4-4), а равенство числа исходов, в результате которых наступают соответствующие события А₁ и А₂ означает равенство их вероятностей Р (А₁) и Р (A₂).

^* (См. Э. Борель, Вероятность и достоверность (перев. с франц.), М., 1964.)

Ошибка де Мере была указана знаменитым Паскалем. Она заключалась в том, что рассматриваемые де Мере исходы вовсе не являются равновероятными. Нужно учитывать не только выпадающие очки, но и то, на каких именно костях они выпали. Например, занумеровав кости и выписывая выпадающие очки в соответствующей последовательности, видно, что комбинация 6-4-1 выпадает, когда наступает один из шести исходов (6, 4, 1), (6, 1, 4), (4, 6, 1), (4, 1, 6), (1, 6, 4), (1, 4, 6), а комбинация 4-4-4 выпадает лишь при одном-единственном исходе (4, 4, 4). Равновероятными в данном опыте являются исходы, описываемые тройками чисел (а, b, с), где а - число очков на первой кости, b - число очков на второй кости, с - число очков на третьей кости. Нетрудно подсчитать, что всего имеется N = 216 равновероятных исходов. Из них событию A₁ - "сумма выпавших очков равна 11" - благоприятствуют N(A₁) = 27 исходов, а событию A₂ - "сумма выпавших очков равна 12" - благоприятствует лишь N(A₂) = 25 исходов. Это и объясняет подмеченную де Мере тенденцию к более частому выпадению 11 очков.

2. При подсчете вероятностей большую пользу оказывают комбинаторные формулы. Приведем наиболее важные из них.

Комбинации элементов, выбираемых из различных групп. Пусть имеется r различных групп, состоящих из каких-либо элементов. Первая группа содержит n₁ элементов a₁, a₂, ..., a_n1, вторая содержит n₂ элементов b₁, b₂, ..., b_n2, ..., последняя r-я группа содержит n_r элементов c₁, с₂, ..., с_nr. Составляются всевозможные комбинации из г элементов, принадлежащих различным группам, так что в отдельную комбинацию входит лишь по одному элементу из каждой группы. Они имеют вид

Комбинации (а, b, ..., с) и (а^~, b^~, ..., с^~) считаются различными, если имеется хотя бы одна пара различных между собой элементов а и a^~, b и b^~, ..., с и с^~. Число всех таких комбинаций есть

Докажем это равенство. При r = 1 оно превращается в тождество. При r = 2 формула (1.2) становится очевидной, если изобразить элементы одной группы точками на оси х, а элементы другой группы - точками на оси у. Тогда всевозможные пары (а, b) изображаются точками прямоугольной "решетки" на плоскости (х, у) и видно, что таких пар всего N = n₁ n₂ (рис. 1). Воспользуемся далее методом математической индукции. Предположим, что формула (1.2) верна, когда число групп не превосходит r-1, и установим ее справедливость для r групп. Пусть имеется r групп. Объединим все возможные комбинации элементов, выбираемых из последних r-1 групп, в одну новую группу. Эти комбинации вида (b, ..., с) примем за новые элементы. По предположению формула (1.2) верна при выборе из r-1 групп, и потому число новых элементов равно произведению n₂ ... n_r. Мы свели случай r групп к случаю, когда имеется лишь две группы, причем пара элементов а и (b, ..., с) - это то же самое, что соответствующая комбинация (а, b, ..., с) исходных элементов. Но мы показали выше, что формула (1.2) верна для двух групп. Следовательно, общее число различных комбинаций вида (а, b, ..., с) равно произведению n₁(n₂ ... n_r), что и требовалось доказать.

Пример. Найдем вероятность того, что при бросании трех игральных костей выпадет максимальное количество очков.

Если обозначить через a, b и с соответствующие очки на первой, второй и третьей костях, то результат бросания можно описать упорядоченной тройкой чисел (а, b, с), каждое из которых выбирается из своей "группы" (принадлежит определенной кости) и пробегает значения от 1 до 6. Таким образом, в каждой из трех "групп" имеется 6 "элементов", и всего насчитывается N = 6³ = 216 всевозможных исходов (а, b, с). Все они равновероятны, а максимальное количество

очков а + b + с = 18 выпадает лишь при одном-единственном исходе, когда а = b = с = 6. Поэтому искомая вероятность равна ¹/₂₁₆.

Выбор с возвращением. Пусть имеется некоторая совокупность n различных предметов а₁, а₂, ..., a_n. Из этой совокупности последовательно выбирается r предметов таким образом, что каждый выбранный предмет фиксируется и возвращается обратно. Результатом такого выбора является комбинация вида

Комбинации (а_i1, a_i2, ..., a_ir) и (а_j1, a_j2, ..., a_jr) считаются различными, если на каком-либо шаге были выбраны разные предметы, т. е. a_ik ≠ a_jk, хотя бы при одном k. Можно представить себе, что имеется r одинаковых групп по n элементов и на k-м шаге выбирается элемент из k-й группы.

Формула (1.2) в этом частном случае дает следующее выражение для числа N различных комбинаций:

Число размещений. Выбор без возвращения. Предположим, что r различных предметов размещаются по некоторым ячейкам. При этом ячейки различимы для наблюдателя и число их равно n. Предположим, что предметы размещаются таким образом, что в каждую ячейку попадает не более одного предмета. Занумеруем все имеющиеся предметы и ячейки. Тогда каждое размещение можно описать комбинацией вида (i₁, i₂,..., i_r), где i₁ - номер ячейки, в которую попадает 1-й предмет, i₂ - номер ячейки, в которую попадает 2-й предмет и т. д., i_r - номер ячейки, в которую попадает последний, r-й, предмет. В комбинации (i₁, i₂, ..., i_r) i₁ - один из n элементов (ячеек), i₂ - один из n-1 оставшихся элементов и т. д., i_r - один из n - r + 1 возможных элементов. Согласно общей формуле (1.2) всего существует

различных размещений r предметов по n ячейкам.

Предположим, что имеется совокупность n различных элементов a₁, a₂, ..., а_n. Из этой совокупности выбирается r элементов. Можно считать, что они выбираются одновременно и располагаются в определенном порядке, а можно считать, что элементы выбираются последовательно один за другим, причем выбранный предмет обратно не возвращается. В результате такого выбора образуется комбинация (а_i1, a_i2, ..., a_ir), где а_i1 - первый из выбранных элементов, a_i2 - второй из выбранных элементов и т. д., а_ir - последний из выбранных элементов; a_i1 может быть любым из n имеющихся элементов, а_i2 - любым из оставшихся n - 1 элементов и т. д., a_ir - любым из n - r + 1 возможных элементов. Всего существует

различных выборок (а_i1, a_i2, ..., a_ir) по r предметов, выбираемых без возвращения из совокупности объема n.

При r = n число размещений совпадает с числом перестановок из n элементов:

Пример. Группа студентов из г человек садится в пригородный электропоезд, насчитывающий n≥r вагонов. Предположим, что каждый из студентов выбирает свой вагон совершенно случайно и с одинаковой вероятностью оказывается в любом из вагонов. Какова вероятность того, что все они попадут в разные вагоны?

Каждый студент может выбрать один из n вагонов, так что всевозможных комбинаций (i₁, i₂, ..., i_r), где i_k - номер вагона, выбранный k-м студентом, насчитывается N = n^r. Событие А - "ни в какой вагон не попало больше одного из рассматриваемых студентов" - наступает тогда и только тогда, когда все элементы i₁, i₂, ..., i_r различны между собой. Можно считать, что совершается выбор (без возвращения) r элементов из совокупности объема n: первый студент выбирает любой из n вагонов, второй - любой из n - 1 оставшихся вагонов и т. д. Следовательно, число комбинаций (i₁, i₂, ..., i_r), приводящих к наступлению события A, составляет N(A) = n(n - 1)...(n - r + 1) и вероятность этого события есть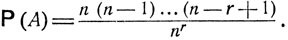

Число сочетаний. Предположим, что размещаются по n ячейкам r неразличимых между собой предметов (в каждую ячейку попадает не более одного предмета). Тогда число различимых размещений совпадает с числом различных групп по r ячеек, которые можно образовать из общей совокупности объема n (в одну группу объединяются все занятые ячейки), и равно числу сочетаний С_n^r из n элементов по r:

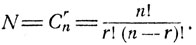
(1.6)

Более общим является случай, когда совокупность из n элементов разбивается на фиксированное число k групп, причем фиксировано и число элементов в каждой группе, скажем, в группе с номером i ровно n_i элементов. В остальном элементы группируются совершенно произвольно. Число различных сочетаний из n элементов по n₁, n₂, ..., n_k элементов (n₁ + n₂ + ... + n_k = n) есть

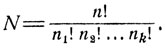
(1.7)

Для доказательства перепишем формулу (1.7) в виде

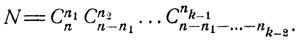
Образование групп можно производить последовательно. Сначала образуем группу в n1 элементов (это можно сделать N1 = Cnn1 различными способами); затем из оставшихся n - n1 элементов образуем группу n2 элементов (это можно сделать N2 = Cn-n1n2 различными способами) и т. д.; остающиеся в конце концов 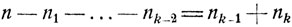элементов можно разбить на две группы по nk-1 и nk элементов Nk-1 = Cnk-1n-n1-...-nk-2 различными способами. Комбинируя на каждом шаге способы образования групп, согласно общей формуле (1.2), в итоге получим указанное число N = N1N2...Nk-1 всех возможных комбинаций.

Пример. Партия из 100 деталей проверяется контролером, который наугад отбирает 10 деталей и определяет их 1 качество. Если среди выбранных контролером изделий нет ни одного бракованного, то вся партия принимается; в противном случае она посылается на дополнительную проверку. Какова вероятность того, что партия деталей, содержащая 10 бракованных изделий, будет принята контролером?

Число всевозможных способов выбрать 10 деталей из партии объемом 100 равно числу сочетаний из 100 по 10 и составляет 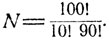Естественно считать, что исходы такого выбора равновероятны. Событие А - "партия деталей принимается контролером" - наступает в том случае, когда все 10 выбираемых наугад деталей образуют группу только из качественных изделий, общее число которых равно 90. Следовательно, число исходов, приводящих к наступлению события А равно числу сочетаний из 90 по 10, что составляет 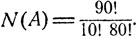Партия принимается, если происходит один из N(A) = C¹⁰₉₀ равновероятных исходов, общее число которых есть N = C¹⁰₁₀₀₀, и вероятность того, что партия будет принята контролером, есть

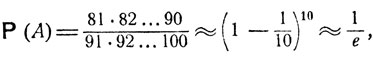
Пример. Рассмотрим игру в преферанс, когда старшие 32 карты карточной колоды случайным образом распределяются (сдаются) между тремя игроками, получающими по 10 карт, и "прикупом", куда кладутся две карты. Какова вероятность того,

что в "прикупе" окажутся два "туза"?

Число различных комбинаций из двух карт, которые могут оказаться в "прикупе", равно числу сочетаний из 32 по 2, что составляет 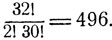В карточной колоде имеется ровно четыре "туза" и число различных комбинаций, дающих два "туза", равно числу сочетаний из 4 по 2, что составляет ^4!/_2!2! = 6. Следовательно, искомая вероятность есть

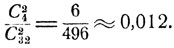
Предположим, что один из игроков - "играющий" - имеет пять старших карт одной масти (скажем, "червей"), исключая "даму". При объявлении ранга игры, "играющему" приходится учитывать возможность образования у одного из противников - "вистующих" - комбинации из трех оставшихся "червей" (так называемую "третью даму"). Какова вероятность этого события?

Всего имеется 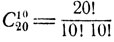равновероятных случаев распределения 20 карт на две равные группы по 10 карт, которые "сдаются" каждому из двух игроков. Если всю комбинацию, "третья дама червей" зафиксировать у какого-либо определенного игрока, то число совместимых с этим случаев распределения равно числу сочетаний из 17 оставшихся карт по 7. Следовательно, вероятность образования у вполне определенного противника "третьей дамы червей" есть

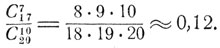
3. Во всех приведенных выше формулах встречается выражение n! = 1*2 ... (n - 1)*n. Существует сравнительно простое асимптотическое соотношение, называемое формулой Стирлинга^*: при больших n

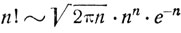
(1.8)

^* (См. В. Феллер, Введение в теорию вероятностей и ее приложения (перев. с англ.), изд. 2-е, М., 1964.)

(здесь и далее соотношение α_n~β_n между переменными величинами α_n и β_n означает, что 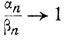при n→∞).