§ 11. Простейшая модель игры двух лиц. Оптимальные стратегии. Одна схема управляемой цепи Маркова. Уравнение Беллмана

1.Пример. Игра с отгадыванием монеты. Рассмотрим следующую игру двух лиц. Один игрок прячет монету достоинством в 10 или 20 копеек, а другой игрок отгадывает, что за монета была спрятана. Если он называет монету правильно, то и получает ее в качестве выигрыша; если он ошибается, то платит 15 копеек. Каковы должны быть стратегии игроков при многократном повторении этой игры?

Пример. Тактика воздушного боя. Предположим, что авиация "красных" совершает налеты на некоторый пункт "белых". При этом каждое отдельное задание выполняется парой самолетов, один из которых несет бомбы, а другой является "прикрывающим". Предположим, что при атаке истребителей "белых" в 20% случаев выбывает из строя тот самолет, что летит первым и находится под защитой основных огневых средств второго самолета, и уже в 40% случаев выбывает из строя самолет, летящий вторым. Пусть истребители "белых" придерживаются той тактики, что атакуют лишь один из самолетов противника. Предположим, что главной боевой задачей для "красных" является бомбардировка объекта, а для "белых" - его прикрытие. В каком порядке должны лететь самолеты "красных" и какой из этих самолетов должны атаковать истребители "белых"?^*

^* (См. Дж. Д. Вильяме, Совершенный стратег (перев. с англ.), М., 1960.)

Эти и многие другие примеры укладываются в следующую простейшую схему игры двух лиц. Именно, каждый игрок может выбрать одну из двух стратегий, определяющих результат игры. При этом интересы игроков противоположны: то, что выигрывает один, фактически проигрывает другой. Такую игру можно описать с помощью таблицы (рис. 12), две строки которой соответствуют двум имеющимся стратегиям первого игрока, два столбца - двум стратегиям второго игрока, а стоящие в клетках числа характеризуют тот выигрыш, который получает первый игрок при выборе каждым из игроков соответствующих стратегий: если первый выбирает i-ю стратегию, а второй - j-ю стратегию (i, j = 1, 2), то выигрыш первого игрока равен v_ij, а выигрыш второго игрока равен - v_ji. Возникает вопрос, какими стратегиями должен руководствоваться каждый из игроков?

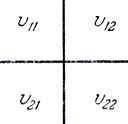
Рис. 12

На этот вопрос легко ответить в случае, когда, скажем,

Ясно, что, как бы ни играл второй игрок, наилучшей возможностью для первого является выбор 1-й стратегии, которая ему обеспечивает выигрыш, равный

При расчете на "умного" противника для второго игрока наилучшей является та стратегия j, при которой наибольший выигрыш противника является минимальным, т. е. та стратегия j, при которой

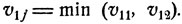
Описанный случай можно считать исключением. Как же поступать в более распространенной и вместе с тем более сложной ситуации, когда соотношения типа (11.0) не имеют места?

Поставим задачу более точно. Предположим, что первый игрок выбирает i-ю стратегию с вероятностью р_1i, а второй игрок выбирает j-ю стратегию с вероятностью p_2j. Распределения вероятносте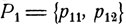й и 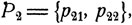с которыми каждый из игроков выбирает соответствующие возможности поведения, называются смешанными стратегиями. При выбранных смешанных стратегиях естественно рассматривать средний выигрыш (первого игрока)

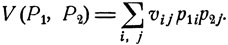
(11.1)

Предположим, что противник первого игрока выбирает наилучший ответ на каждую его стратегию 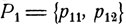, т. е. такую стратегию 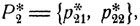что выигрыш первого игрока при выбранной им стратегии Р₁ является минимальным:

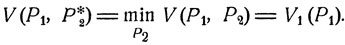
(11.2)

Если считать, что противник играет наилучшим образом, то при стратегии Р₁ первый игрок получает средний выигрыш V₁(P₁), и наилучшей смешанной стратегией для него является то распределение вероятностей 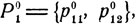для которого

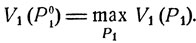
(11.3)

Совершенно аналогичные рассуждения применимы и на месте второго игрока, для которого наилучшей является стратегия Р⁰₂, обеспечивающая максимальный средний выигрыш при расчете на наилучшую игру противника:

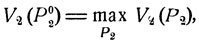
где

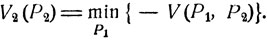
Найдем оптимальные стратегииР⁰₁ и Р⁰₂ для каждого из игроков. Рассмотрим функцию

При х = р₁₁ и y = р₂₁ эта функция численно равна среднему выигрышу первого игрока, когда выбираются смешанные стратеги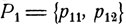и и 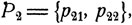. Функция V(x, y) является линейной по каждому из переменных х и y, 0≤х, y≤1. Следовательно, при каждом фиксированном х она достигает своего минимума в одной из крайних точек y = 0 или y = 1:

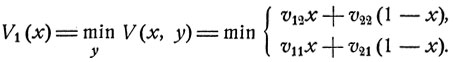
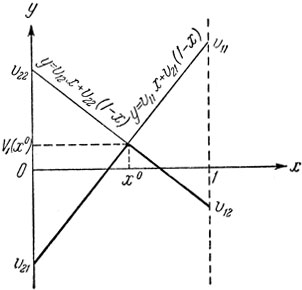
Рис. 13. min (v₁₁, v₁₂)≤max (v₂₁, v₂₂).

Как видно из рис. 13, график функции V₁ (x) является ломаной с вершиной в точке x⁰, определяемой из уравнения

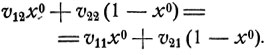
Имеем

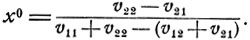
Точка х⁰ - точка максимума функции V₁ (х), 0≤x≤1,- и есть та оптимальная вероятность p⁰₁₁, с которой первый игрок должен выбирать 1-ю стратегию.

Соответствующая смешанная стратегия 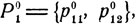обеспечивает наибольший средний выигрыш при расчете на самую лучшую игру противника. Этот выигрыш есть

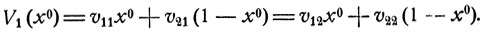
(11.5)

Каково бы ни было y, 0≤y≤1,

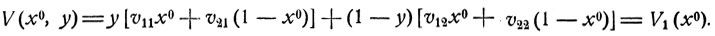
Видно, что при оптимальной вероятности р⁰₁₁ = х⁰, как бы ни играл противник (каково бы ни было y), первый игрок обеспечивает себе средний выигрыш V₁ (х⁰). Если же он отклоняется от оптимальной стратегии р⁰₁₁ = х⁰, выбирая р₁₁ = х, то при подходящем ответе противника, когда р₂₁ = y есть y = 0 или y = 1, средний выигрыш первого игрока уменьшается до величины V₁ (x).

Те же самые рассуждения применимы и на месте второго игрока, для которого оптимальное значение вероятности р⁰₂₁ = y⁰ есть

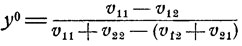
(оно получается из формулы (11.4), если игроков поменять местами, т. е. поменять местами индексы 1 и 2). Так же как и в случае первого игрока, при оптимальной вероятности р⁰₂₁ = y⁰ второй игрок обеспечивает средний выигрыш V₂(y⁰) независимо от стратегии противника:

Отсюда, в частности, вытекает, что

Вернемся к рассмотренным ранее примерам.

Игра с отгадыванием монеты. Здесь следует положить

Оптимальное значение вероятности р⁰₁₁ = х⁰, с которой надо прятать 10-копеечную монету (в предложенной схеме это 1-я стратегия первого игрока), согласно общей формуле (11.4) есть

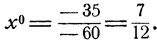
Оптимальное значение вероятности y⁰ = р⁰₂₁, с которой надо называть при отгадывании именно 10-копеечную монету (это 1-я стратегия второго игрока), согласно общей формуле (11.6), есть

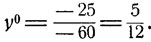
Таким образом, оптимальное поведение первого игрока состоит в том, что он с вероятностью 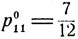прячет 10-копеечную монету, а с вероятностью 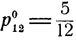- 20-копеечную монету. Оптимальное поведение второго игрока состоит в том, что он с вероятностью 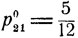называет 10-копеечную 7 монету, а с вероятностью 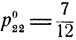- 20-копеечную монету. При этом средний выигрыш первого игрока составит величину

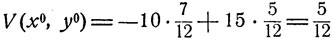
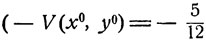
будет, следовательно, выигрыш второго игрока).

Видно, что описанная игра является невыгодной для второго игрока, даже при наилучшем поведении каждый раз проигрывающего в среднем ⁵/₁₂ коп. Всякое же отклонение от этого наилучшего поведения при соответствующем ответе противника только приведет к большему проигрышу.

Тактика воздушного боя. В "игре" с бомбардировщиками "красных" и истребителями "белых" имеется две стратегии каждой из сторон: первым летит самолет с бомбами, первым летит прикрывающий, и атакуется первый самолет, атакуется второй самолет. Если определить выигрыш "красных" как вероятность выполнения боевой задачи - бомбардировки объекта, то следует положить v₁₁ = 0,8, v₁₂ = 1, v₂₁ = 1, v₂₂ = 0,6. По формулам (11.4) и (11.6) находим, что

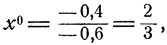
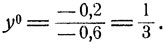
Видно, что для "красных" вовсе не будет наилучшим вариантом максимально обеспечивать безопасность самолета с бомбами, прикрывая его следующим за ним самолетом. Если так поступать всегда, то "белые" в ответ будут всегда атаковать первый самолет, в результате чего вероятность выполнения боевой задачи (вероятность того, что самолет с бомбами не выйдет из строя) будет равна 0,8. Если же, согласно оптимальной смешанной стратегии, поступать так лишь с вероятностью 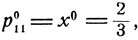то при любой стратегии "белых" эта вероятность будет не меньше, чем

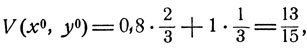
так что вероятность выполнения боевой задачи увеличивается на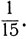

Оптимальная стратегия для "белых" состоит в том, чтобы атаковать первый самолет с вероятностью 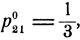а второй - с вероятностью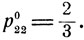

2. Будем условно говорить о некоторой физической системе, шаг за шагом меняющей свое фазовое состояние. Обозначим ε₁, ε₂, ... ее возможные состояния и ξ(t) - ее состояние через t шагов. Будем считать, что процесс эволюции системы, описываемый цепочкой переходов

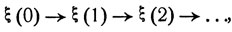
является случайным марковским процессом, причем вероятности р_ij перехода из состояния ε_i в соответствующие состояния ε_j зависят от некоторого управляющего параметра, так что, если система на каком-либо шаге находится в состоянии ε_i и в соответствии с этим наблюдатель выбирает определенное значение управляющего параметра d, то вероятности перехода на следующем шаге будут p_ij = p_ij(d). Совокупность возможных значений управляющего параметра d обозначим D.

Предположим, что задача регулирования такого управляемого случайного процесса состоит в том, чтобы привести систему в определенное фазовое состояние или в одно из состояний определенного множества Е. Поскольку течение процесса ξ(t) зависит не только от воли управляющего этим процессом оператора, но и от случая, привести систему в одно из фазовых состояний указанного множества Е, вообще говоря, можно лишь с некоторой вероятностью Р, зависящей от способа управления.

Предположим, что управляющий процессом оператор руководствуется следующей программой управления: для каждого состояния ε_i, куда система может прийти на некотором шаге n, предусматривается выбор соответствующего значения управляющего параметра d - для каждой пары ε_i и n свое значение d = d(ε_i, n). Вся программа может быть описана функцией d = d(x, t) от х = ε₁, ε₂, ... и t = 0, 1, ..., называемой решающей функцией. Если выбрана программа управления с решающей функцией d = d(x, t), то течение случайного процесса ξ(t) происходит таким образом, что при попадании на n-м шаге в состояние ε_i, на следующем шаге с вероятностями p_ij = p_ij(d), d = d(ε_i, n), осуществляется переход в соответствующие состояния ε_j, j = 1, 2,...

Ясно, что вероятность того, что система будет приведена в одно из заданных состояний, зависит от выбора программы управления, от выбора решающей функции d = d(x, t):

(Управление с решающей функцией d⁰ = d⁰ (х, t) называется оптимальным, если

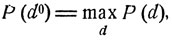
(11.8)

где max берется по всем возможным управлениям, по всем возможным решающим функциям d = d(x, t).

Рассмотрим следующую задачу управления случайным процессом ξ(t): через заданное число шагов п с максимально возможной вероятностью привести систему в определенное множество фазовых состояний Е. В этом случае

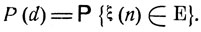
Пусть P(k, i, d) есть вероятность того, что при попадании на k-м шаге в состояние ε_i система за оставшиеся n-k шагов будет приведена в одно из состояний заданного множества Е (при этом считается выбранным некоторое управление d = d(x, t)):

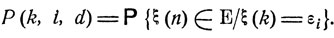
Имеет место следующее соотношение:

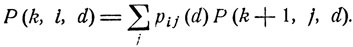
(11.9)

Оно является простым следствием формулы полной вероятности - на следующем шаге система с вероятностью p_ij (d), d = d(ε_i, k), переходит в одно из состояний ε_j, j = 1, 2,..., откуда приводится в множество Е с соответствующими вероятностями P(k+1, j, d).

В соотношении (11.9) при k = n-1 фигурирует вероятность

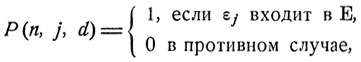
и, следовательно,

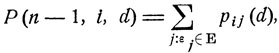
где суммирование идет по всем j, для которых ε_j входит в заданную совокупность Е. Очевидно, вероятность Р (n-1, i, d) зависит лишь от выбора одного-единственного значения управляющего параметра d(ε_i, n-1). Определим d° как точку максимума функции

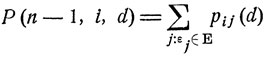
от параметра d, пробегающего множество D:

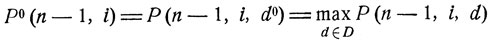
(11.10)

(здесь и в дальнейшем предполагается, что рассматриваемые функции от d достигают максимума). Ясно, что для каждой пары (ε_i, n-1) будет свое значение d⁰ = d⁰(ε_i, n-1), i = 1, 2,...

При k = n-2 формула (11.9) дает следующее соотношение:

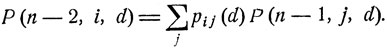
Здесь вероятности p_ij(d) зависят лишь от значений d = d (ε_i, n-2) решающей функции d = d(x, t), а вероятности Р(n-1, j, d) - лишь от исходных значений d = d(ε_j, n-1) этой функции. Если "подправить" решающую функцию d = d(x, t), заменив исходные значения d(ε_j, n-1) на определенные ранее значения d⁰(ε_j, n-1), то от этого соответствующие вероятности Р (n-1, j, d) увеличатся до максимально возможных значений Р⁰(n-1, j), что приведет к увеличению вероятности Р (n-2, j, d) до значения

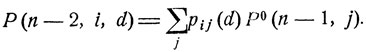
(11.11)

Зависимость от управляющей функции d = d(x, t) здесь проявляется лишь через зависимость переходных вероятностей p_ij(d) от управляющего параметра d = d(ε_i, n-2). Определим точку d⁰ как точку максимума функции от параметра d, пробегающего множество D:

P⁰(n-2, i) = P(n-2, i, d⁰) = 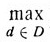P(n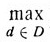-2, i, d)(11.12)

Очевидно, для каждой пары (ε, n - 2) будет свое значение d = d (ε_i, n-2), i = 1, 2, ... Ясно, что если решающая функция d = d(x, t) при х = ε₁, ε₂, ... и t = n-2, n-1 принимает определенные выше значения d⁰(x, t), то вероятности P(k, i, d) при k = n-2, n-1 и всех i = 1, 2,... принимают максимально возможные значения P⁰(k, i).

Отправляясь от решающей функции d = d(x, t) такой, что

при всех х = ε₁, ε₂, ... и t = n-2, n-1, переходим затем к следующему соотношению:

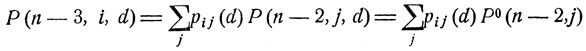
и определяем точку d⁰ = d⁰ (ε_i, n-3) максимума вероятности P(n-3, i, d) как функции от параметра d. Затем, так же как и ранее, "подправляем" решающую функцию d = d(x,t), определяя при t = n-3 ее значения формулой (11.13) для всех х = ε₁, ε₂, ...

Продолжая этот процесс, можно последовательно найти оптимальную решающую функцию d = d⁰(x, t), x = ε₁, ε₂, ..., t = 0, 1, ... , при которой вероятность P(d) = P(0, i, d), отвечающая начальному положению ξ(0) = ε_i, достигает своего максимального значения. На k-м шаге этого последовательного процесса соответствующее значение d⁰ = d⁰(ε_i, n-k) определяется как точка максимума функции

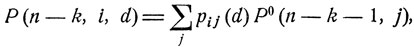
(11.14)

где Р⁰(k, i) суть максимально возможные значения рассматриваемых вероятностей Р (k, i, d); k = 0, 1, ... , n; i = 1, 2, ... Соотношение

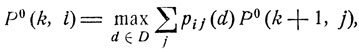
(11.15)

лежащее в основе описанного выше метода нахождения оптимальной решающей функции d⁰ = d⁰(x, t), называется уравнением Беллмана.

Пример. Пусть имеются два возможных состояния ε₁ и ε₂, причем в зависимости от управляющего параметра d переходные вероятности могут непрерывно меняться в пределах α₁≤p₁₁(d)≤β₁, α₂≤p₂₁(d)≤β₂. Как выглядит оптимальное управление, если требуется, чтобы в определенный момент (скажем, через два шага) система была в состоянии ε₁?

В этом случае

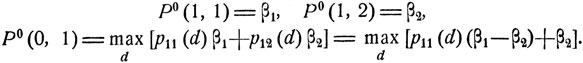
Видно, что, отправляясь из состояния ε₁ следует выбрать максимальной переходную вероятность р₁₁, если β₁≥β₂ (положив p₁₁ = β₁), И выбрать максимальной переходную вероятность р₁₂ = 1-р₁₁, если β₁≤β₂ (положив р₁₁ = α₁). Аналогично выглядит оптимальное решение для начального состояния ε₂.

Задача о наилучшем выборе (см. п. 1 § 3). Рассмотрим описанную ранее процедуру выбора и отвечающий ей марковский случайный процесс с переходными вероятностями р_ij вида (см. стр. 76):

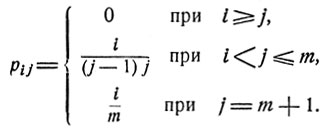
Выбор ξ(k)-го предмета можно интерпретировать как остановку соответствующего процесса

В каждом из состояний ε₁, ... , ε_m наблюдатель решает, остановить или продолжать процесс выбора. Первому решению, принятому в состоянии ε_i, формально соответствуют переходные вероятности p_ij вида

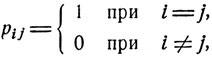
а второму решению - переходные вероятности, указанные ранее. Перед нами схема управляемого марковского процесса, переходные вероятности р_ij которого меняются в зависимости от решения наблюдателя. Управляющий параметр d здесь принимает два значения, скажем 0, что означает остановку процесса в соответствующем состоянии, и 1, что означает принятие противоположного решения. Зависимость переходных вероятностей p_ij = p_ij(d) указана выше. Каждая процедура выбора описывается некоторой решающей функцией d = d(x), х = ε₁, ... , ε_m, которая предусматривает, в каком состоянии х следует продолжать процесс выбора, а в каком следует его прекратить и остановиться на последнем из осмотренных предметов. Задача состоит в том, чтобы найти такую процедуру выбора, такую решающую функцию d = d(x), х = ε₁, ... , ε_m, чтобы вероятность выбрать абсолютно наилучший предмет была бы максимальной. Эта вероятность есть

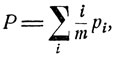
(11.16)

где ⁱ/_m - вероятность того, что 1-й предмет будет наилучшим, p_i - вероятность того, что процесс будет остановлен именно в состоянии ε_i, а суммирование происходит по всем тем состояниям ε_j, в которых, согласно решающей функции d = d(x), предписывается остановка процесса. Эта вероятность зависит от выбранной решающей функции d = d(x).

Для нахождения оптимальной решающей функции d⁰ = d⁰(x) рассмотрим вероятности P(k, d) выбрать наилучший предмет при условии, что число осмотренных до него предметов не меньше k, т. е. при условии, что рассматриваемый процесс на некотором шаге будет в состоянии ε_k. Согласно формуле полной вероятности

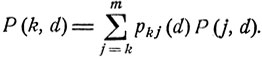
(11.17)

Очевидно, если процесс будет в состоянии ε_m, то m-й предмет и является наилучшим, так что оптимальным значением d = d⁰(ε_m) решающей функции d = d (х) является d⁰ (ε_m) = 0, при котором P(m,d) = 1. Из соотношений (11.16), (11.17) получаем, что при k = m-1 вероятность наилучшего выбора при значении d(ε_m) = 1 есть

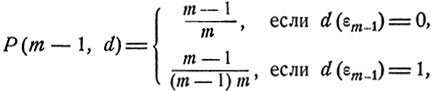
откуда видно, что оптимальным значением d = d⁰(ε_m-1) решающей функции d = d(x) является d⁰(ε_m-1) = 0. При этом 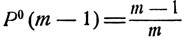есть максимально возможное значение вероятности Р(m-1, d), зависящей от решающей функции d = d (х).

Предположим, что при x = ε_k, ... , ε_m оптимальные значения решающей функции d = d(x) все равны 0, что соответствует остановке процесса в состояниях ε_k, ... , ε_m. Каково предшествующее оптимальное значение d⁰(ε_k-1)?

Очевидно, если процесс останавливается в любом из состояний x = ε_k, ... , ε_m, то, как следует из соотношений (11.16), (11.17), вероятность наилучшего выбора при условии, что будет осмотрено не менее k-1 предметов, есть

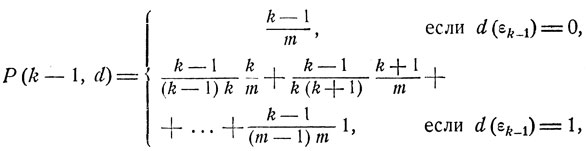
откуда видно, что оптимальное значение d = d⁰(ε_k-1) решающей функции d = d(x) есть

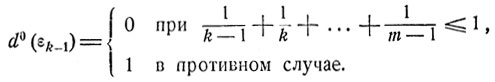
(11.18)

Легко видеть, что оптимальная решающая функция d = d(x) имеет следующую структуру:

где m₀ - некоторое число. При оптимальном выборе следует продолжать процесс осмотра до тех пор, пока не попадется предмет с номером k≤m₀, наилучший среди всех ранее осмотренных предметов. На этом k-м по счету предмете и следует остановить свой выбор. Согласно (11.18) число m₀ есть наибольшее натуральное число, для которого

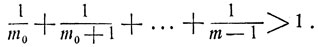
Нетрудно установить, что при больших m это число m₀ приблизительно равно ^m/_e, e = 2,78 ...