Дополнение I. Полиномы Чебышева

Мы видели в § 12, что при любом целом n функция cos n (arc cos х) определенная на [-1, 1], совпадает на этом сегменте с некоторым многочленом степени n. Эти многочлены носят название полиномов Чебышева, по имени великого русского математика, и обозначаются символом Т_n(х). Согласно результатам, полученным в § 12, имеем:

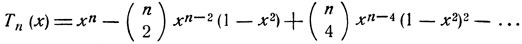
В настоящем дополнении мы остановимся на некоторых замечательных свойствах полиномов Чебышева. Выведем рекуррентную формулу, позволяющую последовательно вычислять полиномы Чебышева.

Чебышев Пафнутий Львович

Положим в тригонометрической формуле:

тогда получим:

Полагая φ = arc cos x, будем иметь:

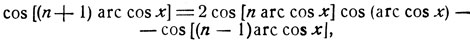
откуда:

Принимая во внимание, что

^* (T₀(x) = 1, так как cos(0 arc sin x) = cos 0 = 1.)

Пользуясь формулой (1), найдем;

Определим значение коэффициента при xⁿ в полиноме Т_n. Легко видеть, что этот коэффициент есть 2^n-1. Докажем это методом полной индукции. В самом деле, для полинома Т_n наше утверждение справедливо. Предположим, что для полинома T_n этот коэффициент равен 2^n-1, тогда, в силу рекуррентной формулы (I), мы видим, что коэффициент при хⁿ⁺¹ полинома T_n+1 есть 2ⁿ. Отсюда следует справедливость высказанного утверждения для любого натурального значения n.

Как и всякий многочлен степени n, Т_n имеет n корней; покажем, что все эти корни действительны и расположены в интервале (-1, 1). В самом деле, в интервале (-1, 1) имеем

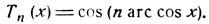
Ясно, что T_n (x) = 0, если

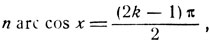
откуда:

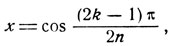
где k - любое целое число.

Придавая k значения 1, 2, 3, ..., n, мы, получаем n корней Т_n(х). Будем эти корни в соответствии с значением k обозначать так: x₁, х₂, ..., х_k, ..., х_n.

Придавая k целые значения, отличные от рассмотренных, мы не получим других корней, кроме найденных. В самом деле:

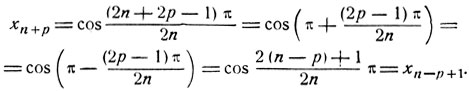
Отсюда мы видим, что x_n+1 = x_n; x_n+2 = x_n-1; x_n+3 = x_n-2; и т. д.

Значения х₁, х₂, ..., x_n являются простыми корнями Т_n (х), ибо среди них нет равных. Для построения корней Т_n можно поступить следующим образом: разделим полуокружность единичного радиуса на 2n равных частей, занумеруем точки деления в направлении, указанном на чертеже 58, и отметим точку Л, ближайшую к точке В с абсциссою 1. Затем, начиная с точки А, спроектируем на отрезок [-1, 1] через одну точки деления (черт. 58). Полученные в проекции точки и являются геометрическим изображением корней полинома Т_n (х),

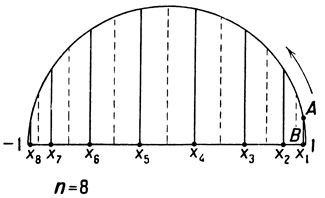
Черт. 58

Если значение х заключено на сегменте [- 1, 1], то (в силу определения) значения полиномов Чебышева заключены на том же сегменте:

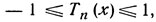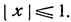если (2)

Определим те значения х на сегменте [-1, 1], для которых Т_n (х) = ±1; так как Т_n (х) = cos (n arc cos x), то

Таким образом,

Отсюда находим:

Итак:

Таким образом, график функции y = Т_n (х) на сегменте [-1, 1] является колеблющейся в пределах [-1, 1] линией, пересекающей в n точках ось абсцисс (черт. 59).

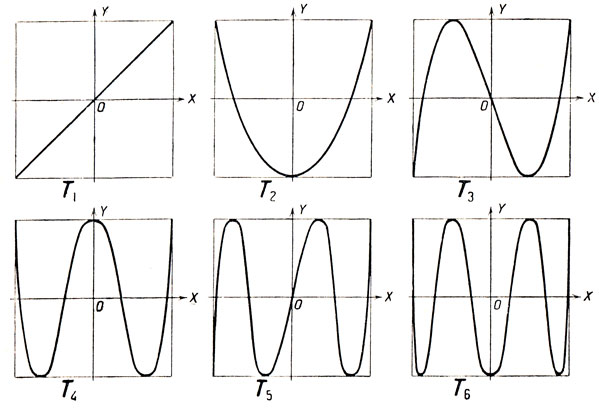
Черт. 59

Рассмотрим многочлен

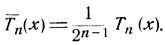
Для каждого из многочленов Т_n (х) коэффициент при х_n равен единице. Этот многочлен, как и Т_n, имеет n корней, расположенных в интервале (-1, 1). На основании неравенств (2) имеем:

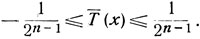
(2')

Рассмотрим одно из важных свойств полиномов Т_n (х).

Предположим, что на некотором сегменте [а, b] дана функция f (х). Пусть с - некоторая точка сегмента [а, b]. Величина |f(c)| характеризует отклонение от нуля значения функции f(х)в данной точке с.

Будем называть отклонением от нуля функции f(x)на сегменте [а, b] наибольшее значение |f(x)| на сегменте [а, b].

Это наибольшее значение обозначается так: max |f(х)|.

Если функция f (х) непрерывна, то непрерывна также и функция |f(х)| и существование наибольшего значения |f(x)| следует из теоремы, которая доказывается в курсе математического анализа.

Эта теорема формулируется следующим образом. Всякая непрерывная на сегменте функция по крайней мере в одной точке этого сегмента имеет наибольшее (наименьшее) значение.

Свойство полиномов Чебышева, о котором будет идти речь, выражается следующей теоремой.

Из всех многочленов степени n, имеющих коэффициент при х_n, равный единице, наименьшее отклонение от нуля на сегменте [-1,1 ] имеет полином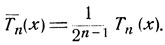

Согласно неравенствам (2') отклонение от нуля полинома 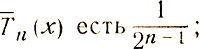предположим, что некоторый многочлен:

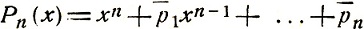
имеет отклонение от нуля на сегменте [-1, 1], не превосходящее отклонения 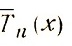. Следовательно, согласно сделанному предположению на сегменте [-1, 1] выполнены неравенства:

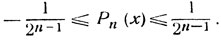
(3)

Рассмотрим точки

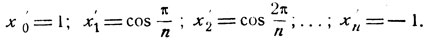
В этих точках имеем:

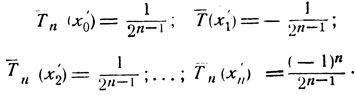
(4)

Разность R(x) = 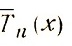- P_n(х) есть многочлен степени не выше n-1. Согласно неравенствам (3) и равенствам (4) будем иметь:

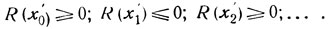
(5)

Сегмент [-1, 1] разбит при помощи точек х'₀, x'₁, х'₂,..., x'_n на n сегментов. Рассмотрим один из этих сегментов; его границами служат две соседние точки x'_i+1 и x'_i. Ясно, что R (х) обращается в нуль по крайней мере в одной точке каждого из сегментов [x'_i+1, x'_i].

В самом деле, если R (x'_i+1)≠0 и R (х'_i)≠0, то в силу условий (5) R (x) на концах сегментов [х_i+1, х_i] имеет разные знаки, а потому в силу непрерывности обращается в нуль по крайней мере в одной внутренней точке данного сегмента. Таким образом, R (х) обращается в нуль по крайней мере в одной внутренней или граничной точке каждого сегмента [x_i+1, x_i]. Отсюда мы заключаем, что R (x) = 0, так как, будучи многочленом степени n-1, он имеет по меньшей мере n корней, а следовательно,

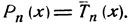
Этими рассуждениями доказано, что полином 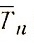является многочленом, наименее уклоняющимся от нуля на сегменте [-1, 1] по сравнению с любым многочленом степени n, имеющим при хⁿ коэффициент, равный единице.