
Глава VIII. О выполнении обратных тригонометрических операций над тригонометрическими функциями
§ 25. Простейшие случаи выполнения обратных тригонометрических операций над тригонометрическими функциями
На вопрос, что представляют собой выражения
arc sin (sin x), arc cos (cos x), arc tg (tg x), arc ctg (ctg x)
нередко дается ошибочный ответ.
Обычно говорят, что при всех значениях х имеем
arc sin (sin x) = x.
При этом обыкновенно дается такое объяснение: арксинус и синус являются взаимно обратными операциями или это есть дуга, синус которой равен синусу х. В подтверждение этих рассуждений обычно проводится аналогия с тождеством:
sin (arc sin x) = x.
Однако надо иметь в виду, что арксинус является обратной функцией относительно функции y = sin x лишь на сегменте 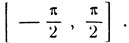
Положим х = π/6. Дуги arc sin 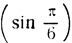 и π/6 имеют одинаковый синус и обе заключены на сегменте
и π/6 имеют одинаковый синус и обе заключены на сегменте 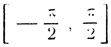
Поэтому
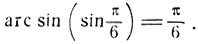
Положим х = 3π/4. В этом случае дуга 3π/4 не расположена на сегменте 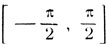 Дуга π-3π/4 расположена на сегменте
Дуга π-3π/4 расположена на сегменте 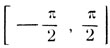 и имеет тот же синус, как и 3π/4 поэтому:
и имеет тот же синус, как и 3π/4 поэтому:
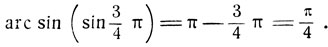
Рассмотрим функцию
y = arc sin (sin х).
В силу периодичности синуса функция arc sin (sin х) также является периодической с периодом 2π, поэтому достаточно исследовать ее на промежутке величиной 2π. В силу определения арксинуса у есть дуга, заключенная на сегменте 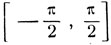 и удовлетворяющая условию:
и удовлетворяющая условию:
sin у = sin х.
если значение х заключено на сегменте 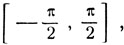 то y = х, и, следовательно, на этом сегменте график функции совпадает с биссектрисой координатного угла. Предположим, что значение х заключено на сегменте
то y = х, и, следовательно, на этом сегменте график функции совпадает с биссектрисой координатного угла. Предположим, что значение х заключено на сегменте 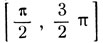 В этом случае дуга π - х заключена на сегменте
В этом случае дуга π - х заключена на сегменте 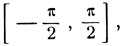 и так как
и так как
sin (π - х) = sin x, то имеем y = π - х,
и, следовательно, в этом промежутке график функции совпадает с прямой линией π - х. Если значение х заключено на сегменте 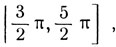 то, пользуясь периодичностью или путем непосредственной проверки, получаем:
то, пользуясь периодичностью или путем непосредственной проверки, получаем:
y = х - 2π.
Если значение х заключено на сегменте 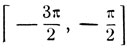 то
то
y = - π - х.
Если значение х заключено на сегменте 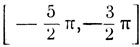 то
то
y = х + 2π.
Вообще, если -π/2+2kπ≤x≤π/2+2kπ то
y = х - 2kπ,
и если π/2 + 2kπ≤ х ≤ 3π/2 + 2kπ, то
y = (π - x) + 2kπ.
Рассмотрение полученных результатов приведет к графику функции y = arc sin (sin x) в виде ломаной, изображенной на чертеже 49.
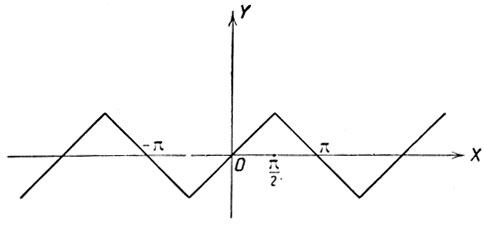
Черт. 49
Рассмотрим функцию
y = arс cos (cos x).
Эта функция периодическая, с периодом 2π. Если значение х заключено на сегменте [0, π], то мы имеем y = х.
Если значение х заключено на сегменте [π, 2π], то дуга 2π - х заключена на сегменте [0, π] и cos (2π - x) = cos x, поэтому:
arc cos (cos x) = 2π - x.
Следовательно, на сегменте [π, 2π] имеем:
y = 2π - х.
Если значение х заключено на сегменте [2π, 3π], то
y = х - 2π.
Если значение х заключено на сегменте [3π, 4π], то
y = 4π - x.
Вообще, если 2kπ≤x≤(2k+1)π, то
y = х - 2kπ,
если же (2k-1)π≤x≤2kπ, то
y = - х + 2kπ.
Графиком функции y = arc cos (cos x) является ломаная линия (черт. 50).
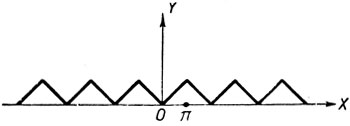
Черт. 50
Рассмотрим функцию y = arc tg (tg x). При изучении этой функции мы должны исключить из рассмотрения значения х вида (2k+1)π/2. Эти значения не являются допустимыми, так как tg (2k+1)π/2 не имеет смысла.
Функция arc tg (tg x) является периодической с периодом π. Из определения следует, что y есть дуга, взятая в интервале (-π/2, π/2) и удовлетворяющая условию
tg y = tg x.
Отсюда ясно, что для всякого значениях, удовлетворяющего неравенствам -π/2<х<π/2 имеем:
y = х.
Предположим, что значение х заключено в интервале (π/2, 3π/2), тогда дуга х - π заключена в интервале (-π/2, π/2) и
tg (x - π) = tg x,
следовательно, в этом интервале имеем:
y = х - π.
Это же можно получить, если воспользоваться периодичностью данной функции. Графиком функции y = arс tg (tg x) в интервале (-π/2, π/2) является отрезок прямой y = х, а в интервале (π/2, 3π/2) - отрезок прямой y = х - π (черт. 51).
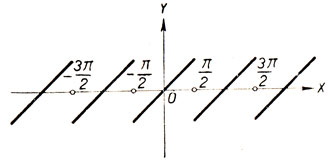
Черт. 51
Для рассматриваемой функции х = π/2 является точкой разрыва.
В самом деле, в этой точке y не имеет предела. Будем рассматривать значения х, достаточно близкие к π/2. Если х<π/2, то y = х, и мы имеем 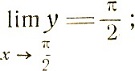 если же х>π/2, то y = х - π, а потому
если же х>π/2, то y = х - π, а потому 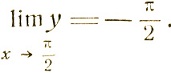
Следовательно, предел y "слева" (т. е. при х<π/2) равен π/2, а предел "справа" (т. е. при х>π/2) равен -π/2, и одного "единого" предела в точке π/2 не существует.
В математическом анализе точка х = а называется точкой разрыва первого рода функции f(х), если существуют отдельно левый предел 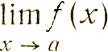 в предположении, что x<а, и правый предел
в предположении, что x<а, и правый предел 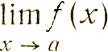 в предположении, что х>а, и эти "односторонние" пределы различны. Таким образом, для функции arc tg (tg x) точка π/2 является точкой разрыва первого рода.
в предположении, что х>а, и эти "односторонние" пределы различны. Таким образом, для функции arc tg (tg x) точка π/2 является точкой разрыва первого рода.
Легко видеть, что:
arc tg (tg x) = x - 2π, если 3π/2<x<5π/2;
и вообще:
arc tg (tg x) = x - kπ, если (2k-1)π/2<x<(2k+1)π/2.
График функции y = arc tg (tg x) построен на чертеже 51.
На чертеже 52 дано геометрическое изображение функции arc ctg (ctg x). Мы не будем подробно останавливаться на соответствующих исследованиях, что может сделать читатель.
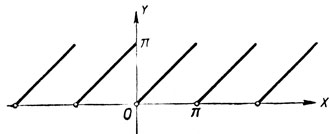
Черт. 52
Отметим, что исследование функций arc cos (sin x) и arc ctg (tg x) не представляет затруднений, так как, пользуясь соотношениями
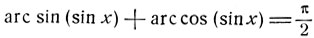
и
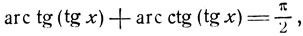
мы можем привести рассмотрение этих функций к уже изученным функциям.
При помощи функций arc sin (sin x) и arc cos (cos x) можно задавать ломаную линию посредством одного уравнения.
Аналогично при помощи функций arc tg (tg x) и arc ctg (ctg x) можно одним уравнением задать разрывную линию, составленную из несоединенных между собой отрезков. Комбинируя эти функции с другими функциями, мы можем в качестве графиков получить разнообразные ломаные и разрывные линии.
Примеры:
1) Исследовать функцию y = х - arc tg (tg x) и построить ее график.
Рассматривая эту функцию в различных промежутках, получим:
если
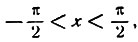
то
arc tg (tg x) = x и y = 0;
если
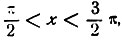
то
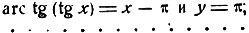
если
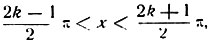
то
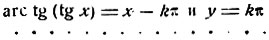
В качестве графика мы получим изображенную на чертеже 53 ступенчатую разрывную линию.
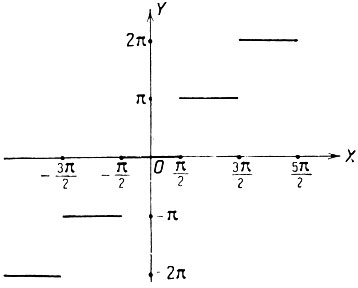
Черт. 53
2) Исследовать функцию y = x - arc sin (sin x) и построить ее график.
тс
Если -π/2≤х≤π/2, то arc sin (sin x) = х и y = 0;
если π/2≤x≤3π/2, то arc sin (sin x) = π - x и y = 2x - π;
если 3π/2≤x≤5π/2, то arc sin (sin х) = х - 2π и y = 2π;
если 5π/2≤x≤7π/2, то arc sin (sin х) = 3π - х и y = 2х - 3π.
В качестве графика мы получаем изображенную на чертеже 54 ломаную линию.
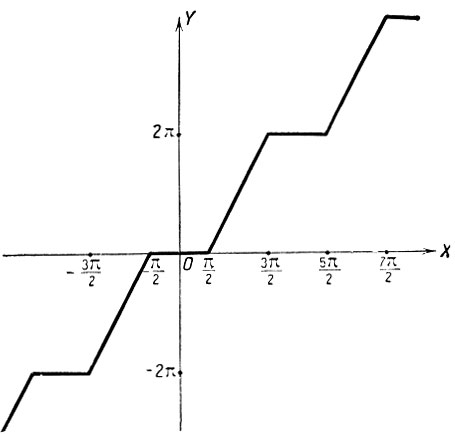
Черт. 54
3) Исследовать функцию y = х arc sin (sin x).
Если -π/2≤x≤π/2, то y = х2;
если π/2≤x≤3π/2, то y = x(π-x);
если 3π/2≤x≤5π/2, то y = х(х-2π);
если 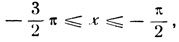 то
то 
В качестве графика мы получим ломаную линию, состоящую из параболических дуг (черт. 55).
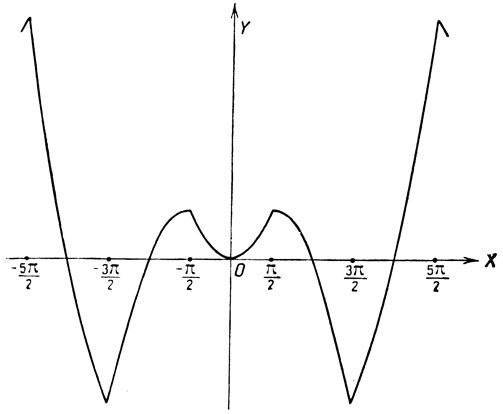
Черт. 55
Упражнения. Исследовать функции:
y = arc tg (tg ч) - arc sin (sin x) (черт. 56).
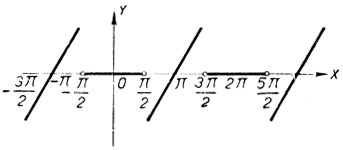
Черт. 56
y = arc cos (cos x) - arc sin (sin x) (черт. 57).
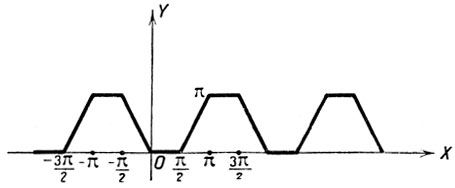
Черт. 57
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'