§ 24. Уравнения, приводящиеся к алгебраическим

Основной прием решения уравнений, содержащих обратные тригонометрические функции, заключается в том, что над обеими частями уравнения производится некоторая тригонометрическая операция. Следует иметь в виду, что выполнение тригонометрической операции над обеими частями уравнения может привести к уравнению, не эквивалентному данному. Возьмем, например, синус от обеих частей уравнения:

тогда получим уравнение:

К тому же уравнению мы придем, если возьмем синус обеих частей уравнения:

при любом целом значении n. Поэтому среди решений уравнения (2), кроме корней уравнения (1), содержатся все корни уравнений вида (3) при любом целом n.

Во многих случаях в результате выполнения какой-либо тригонометрической операции над обеими частями уравнения, содержащего аркфункций, получается алгебраическое уравнение. В каждом таком случае корни данного уравнения содержатся среди корней алгебраического уравнения. Следовательно, для решения данного уравнения достаточно найти все решения алгебраического уравнения в поле действительных чисел и подвергнуть их проверке посредством подстановки в исходное уравнение. Проверка корней необходима, так как выполнение тригонометрической операции может внести "посторонние" решения.

Алгебраические функции, получающиеся в результате выполнения тригонометрических операций над аркфункциями, вообще говоря, являются иррациональными (см. гл. III). Следовательно, алгебраические уравнения, получающиеся после выполнения тригонометрических операций над обеими частями данного уравнения, в общем случае будут также иррациональными. Освобождение иррационального уравнения от радикалов также может привести к появлению посторонних решений.

На нижеследующих примерах пояснены различные приемы решения уравнений, содержащих обратные тригонометрические функции.

1) Решить уравнение:

Возьмем синус от обеих частей:

откуда

или

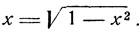
(5)

Возводя в квадрат обе части, получим:

откуда

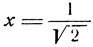
и

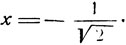
Значение 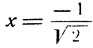не есть корень иррационального уравнения (5). Это есть "постороннее" решение, появившееся в результате возведения в квадрат обеих частей уравнения (4).

Значение 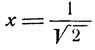есть корень иррационального уравнения, но не есть решение данного уравнения (4), так как данное уравнение не имеет решений. В самом деле, предположив противное, мы придем к противоречию с тождеством:

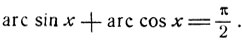
Значение 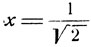удовлетворяет другому уравнению:

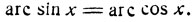
Если взять синус от обеих частей этого последнего уравнения, то получится то же самое иррациональное уравнение. 2) Решить уравнение: arc sin mx = arc cos nx. Для получения алгебраического уравнения, которому должно удовлетворять неизвестное, произведем над обеими частями данного уравнения какую-нибудь тригонометрическую операцию. Поступим, например, так:

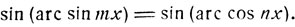
Откуда (на основании формул § 11) получим иррациональное уравнение:

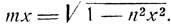
По возведении обеих частей в квадрат, получим:

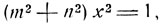
откуда

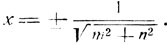
Исследуем, являются ли найденные значения х решениями данного уравнения. Рассмотрим следующие случаи:

а) m≥0; n≥0, но по крайней мере одно из чисел m или n отлично от нуля. В этом случае уравнению может удовлетворить только положительное значение х, так как при х≤0 дуги arc sin mx и arc cos nx расположены в различных промежутках:

и

Поэтому предложенное уравнение не может иметь отрицательных решений. Легко видеть, что единственным решением данного уравнения является:

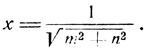
b) m≤0; n≤0, но по крайней мере одно из чисел m или n отлично от нуля. В этом случае уравнение не может иметь положительных решений, и единственным его решением является:

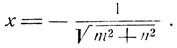
В этом случае предложенное уравнение не имеет решений, так как аргументы аркфункций mх и nх имеют разные знаки, а поэтому дуги arc sin mx и arc cos nx расположены в различных промежутках. То же самое можно сказать и в случае m<0; n>0.

d) m = n = 0. В этом случае уравнение противоречиво.

3) Решить уравнение:

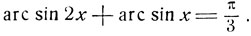
(6)

Приравнивая косинусы обеих частей, получим алгебраическое уравнение:

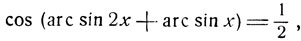
откуда:

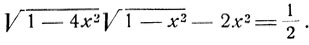
Освобождая последнее уравнение от радикалов, получим:

Среди корней этого квадратного уравнения находятся решения уравнения (6). Решая квадратное уравнение, получим:

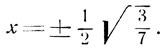
Значение 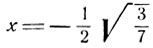не может служить корнем данного уравнения. В самом деле, дуг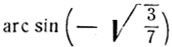и и 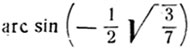расположены в промежутке 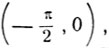и поэтому их сумма не может равняться ^π/₃. Значение 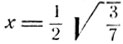является решением данного уравнения. В этом можно убедиться проверкой. В самом деле, подставим в левую часть данного уравнения 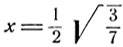и воспользуемся формулой суммы арксинусов:

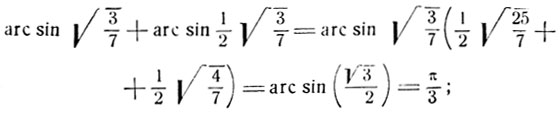
в нашем случае

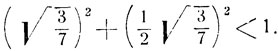
Примечание. Мы пришли к алгебраическому уравнению путем взятия косинуса от обеих частей; ясно, что можно прийти к алгебраическому уравнению, если выполнить над обеими частями какую-нибудь другую тригонометрическую операцию. Взятие косинуса наиболее удобно (в данном случае), так как получается только одно слагаемое, содержащее радикалы, что позволяет освободить уравнение от иррациональности однократным возведением в квадрат обеих частей.

4) Решить уравнение:

Взяв тангенс от обеих частей, получим квадратное уравнение

которое имеет корни

Оба найденные значения удовлетворяют уравнению.

5) Решить уравнение:

Данное уравнение равносильно следующему уравнению:

откуда:

Приравнивая косинусы обеих частей, получим:

откуда:

Корни полученного уравнения суть х = 0 и x = ¹/₂. Производя подстановку в данное уравнение, мы видим, что ему удовлетворяет только первый корень х = 0. Второе же значение х = ¹/₂ является решением другого уравнения:

Уравнение (8) получается из уравнения (7), если замените

6) Решить уравнение:

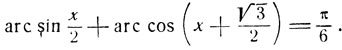
(9)

Взяв синус от обеих частей и освобождая от радикалов полученное иррациональное уравнение, придем к квадратному уравнению

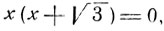
откуда: х = 0 и х = -√3.

Уравнению (9) удовлетворяет только значение x = 0. Значение х = -√3 удовлетворяет другому уравнению:

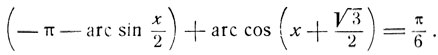
(10)

Уравнение (10) может быть получено из уравнения (9) заменой

Корни уравнений (9) и (10) удовлетворяют одному и тому же квадратному уравнению 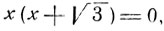. Именно, х = 0 удовлетворяет уравнению (9), но не удовлетворяет уравнению (10), а х = -√3 удовлетворяет уравнению (10), но не удовлетворяет уравнению (9).

7) Решить уравнение:

Взяв тангенс от обеих частей, получим:

откуда:

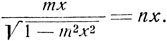
Это уравнение имеет очевидное решение х = 0. Для отыскания других решений имеем уравнение m²n²x² = n²-m², откуда при m≠0 и n≠0 получим:

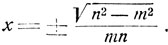
Уравнение (11) не имеет других решений, кроме х = 0 в случаях а также если знаки чисел тип противоположны. Если числа m и n противоположных знаков и 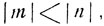то найденные значения служат корнями уравнения:

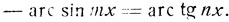
Последнему уравнению соответствует иррациональное уравнение:

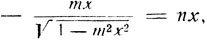
которое после освобождения от радикалов приведет к тому же квадратному уравнению:

Если m = 0, но n≠0, то уравнение (11) примет вид:

которое имеет единственное решение х = 0.

Если n = 0, но m≠0, то получим единственное решение х = 0.

Если m = n = 0, то уравнение удовлетворяется тождественно всеми значениями х.

8) Решить уравнение:

имеем:

откуда

следовательно:

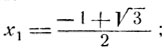
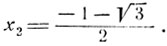
Так как 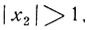то х₂ не может служить корнем данного уравнения.

Число х₁ является решением уравнения (12), так как дуги 2 arc sin х₁ и arc cos 2х₁ расположены в промежутке (0, π) и имеют одинаковый косинус (x₁>0).

9) Решить уравнение:

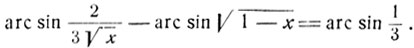
Приравнивая синусы обеих частей, получим:

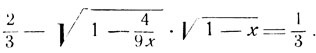
После освобождения от радикалов и элементарных преобразований будем иметь квадратное уравнение: ?

Это уравнение имеет двукратный корень х = ²/₃. Подстановкой легко убедиться, что найденное значение удовлетворяет уравнению. Мы пришли бы к тому же квадратному уравнению, если бы стали рассматривать уравнение:

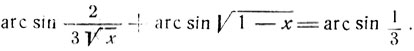
Однако значение х = ²/₃ не удовлетворяет последнему уравнению. В этом случае иррациональное уравнение принимает вид:

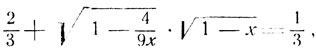
а это последнее уравнение решений не имеет.

10) Решить уравнение:

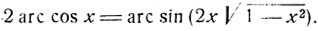
Имеем:

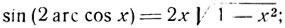
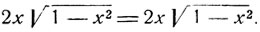
Мы пришли к тождеству, однако это еще не значит, что данное уравнение удовлетворяется при всех значениях х.

В самом деле, при значениях 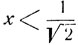уравнение не может удовлетвориться, так как при этих значениях:

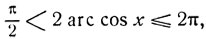
тогда как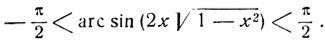

Уравнение имеет бесконечное множество решений, именно ему удовлетворяет любое значение х на сегменте:

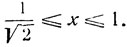
11) Решить уравнение:

Имеем x = cos(arc tg x); x = ¹/_√(x²+1)

откуда:

Последнее уравнение имеет два действительных корня:

и

из которых данному уравнению удовлетворяет первый.

Отметим следующие простейшие случаи, когда можно получить квадратное уравнение, среди корней которого содержатся корни уравнения, содержащего аркфункции:

1) arc sin(mx+p) + arc sin(nx+q) = a.

Приравнивая косинусы обеих частей и освобождаясь от радикалов, получаем квадратное уравнение:

2) arc cos (mx+p) + arc cos (nx+q) = a.

Поступая подобным же образом, придем к квадратному уравнению:

3) arc tg(mx+p) + arc tg(nx+q) = a.

Взяв тангенс от обеих частей, получим:

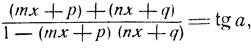
откуда получим квадратное уравнение:

Пользуясь формулами:

мы можем привести к уравнениям рассмотренного вида следующие уравнения:

Укажем ряд простейших уравнений, решение которых может быть приведено к решению уравнений высших степеней.

и т. д.

где m и n - целые числа, а а; b; с;... - некоторые данные действительные числа. Рассмотрим более подробно первое из написанных уравнений. Приравнивая синусы обеих частей, получим

откуда:

Мы видели в § 12, что каждая из функций

является алгебраической, а поэтому уравнение (13) является алгебраическим. Ясно, что указанным путем можно свести к решению алгебраического уравнения решение любого из уравнений этого же вида, в котором под знаком аркфункций содержатся не обязательно линейные, а какие-либо другие алгебраические функции.