Глава VII. Уравнения, содержащие неизвестное под знаком аркфункций

§ 23. Простейшие уравнения

Простейшими уравнениями мы будем называть уравнения вида:

в которых требуется найти неизвестное по заданному значению одной из аркфункций. Рассмотрим подробнее одно из этих уравнений. Возьмем, например, первое уравнение

Это уравнение не всегда имеет решение. В самом деле, значения функции arc sin x заключены на сегменте 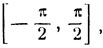а поэтому данное уравнение может иметь решение только в том случае, если выполнено неравенство |m|≤^π/₂. При соблюдении этого условия получаем единственное решение уравнения:

Аналогично рассматриваются прочие простейшие уравнения. Уравнение

имеет единственное решение:

при условии 0≤m≤π и не имеет решений, если m не принадлежит сегменту [0, π].

Уравнение

имеет единственное решение:

при условии, если m принадлежит интервалу (-^π/₂, ^π/₂).

Уравнение

имеет единственное решение:

если m принадлежит интервалу (0, π). Непосредственно приводятся к простейшим уравнения линейные относительно аркфункции, под знаком которой содержится неизвестное. В качестве примера рассмотрим уравнение

Решая это уравнение относительно arc sin x, получим

или, полагая

придем к простейшему уравнению:

Не представляет затруднений рассмотрение уравнений, в которых под знаком аркфункции содержится какая-либо функция от неизвестного. Так, например, уравнение

где

равносильно уравнению

не содержащему аркфункции.

Примеры:

1) 6 arc sin x - π = 0.

Решение. x = sin ^π/₆ = ¹/₂.

2) 2 arc sin х - 8 = 0.

Так как 4>^π/₂, то уравнение не имеет решении.

3) Решить уравнение

Решение.

arc sin √х = ^π/₃, √х = ^√3/₂,

откуда

4) Решить уравнение

Решение.

откуда

Рассмотрим уравнение, в котором неизвестное содержится под знаком лишь одной аркфункции. Возьмем, например, уравнение:

Введем новое неизвестное y = arc sin x, тогда получим:

Пусть y₁; y₂; ... - корни уравнения f(y) = 0, тогда корни уравнения f(arc sin х) = 0 находятся путем решения простейших уравнений:

arc sin x = y₁; arc sin х = y₂; ... Решим, например, уравнение

Корни квадратного уравнения

суть

Из двух простейших уравнений

только второе дает решение данного уравнения

Первое не имеет решений: ибо 2>^π/₂

Уравнение

содержащее неизвестное под знаками арксинуса и арккосинуса, приводится к уравнению рассмотренного типа. В самом деле, воспользовавшись тождеством

можно выразить одну из аркфункций через другую и, подставив в данное уравнение, получить уравнение, содержащее лишь одну аркфункцию. Это же замечание относится к уравнениям вида

Рассмотрим, например, уравнение

заменяя в этом уравнении arc cos х через ^π/₂ - arc sin x получим

или

откуда

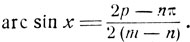
Уравнение имеет решение только при выполнении условия

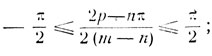
при указанном условии получим

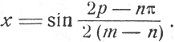
Пример.

Решение.4 arc tg x - 6(^π/₂ - arc tg x) = π; 10 arc tg x = 4π и x = tg ^2π/₅.