§ 22. Особые случаи решения уравнений

Рассмотрим уравнение

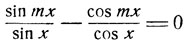
(где m ≠ 1).

Приводя к общему знаменателю и выполняя несложные преобразования, получим:

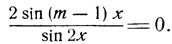
Дробь равна нулю, если ее числитель равен нулю, следовательно,

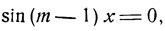
однако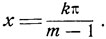

Однако при найденных значениях х, обращающих в нуль числитель, может обратиться в нуль знаменатель, и тогда левая часть потеряет смысл. Следовательно, из множества найденных значений придется исключить те значения, которые обращают в нуль знаменатель, т. е. значения вида ^lπ/₂, где l - любое целое число. Но если есть целое число. Так, если m = 2, то 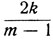всегда целое число, а потому все полученные значения исключаются. Если, например, m = 4, то ^2k/₃ не есть целое число, если k кратное числа 3, эти значения для k придется исключить. Если 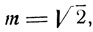то 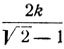не есть целое число ни при каком k, a потому все найденные значения удовлетворяют уравнению. Таким образом, приравнивая нулю числитель или отдельные сомножители левой части уравнения f(x) = 0, можно получить значения, при которых левая часть теряет смысл, эти значения следует исключать из рассмотрения.

Рассмотрим уравнение

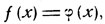
(1)

в котором правая и левая части заданы при помощи некоторых аналитических выражений. Пусть при значении х = а хотя бы одно из выражений f(х) или φ(x) утрачивает смысл. Если основываться f непосредственно на определении корня уравнения как такого значения аргумента, при котором значения функций f(х) и φ(х) равны, то число а нельзя считать принадлежащим множеству допустимых значений неизвестного, а значит нельзя его считать корнем уравнения. Однако в некоторых

"особых" случаях оказывается целесообразным расширить понятие корня уравнения.

Примем следующее дополнительное определение корня в особом случае.

Определение. Если в точке а хотя бы одно из выражений f(х) и φ(х) теряет смысл и если предел разности f(х) - φ(х) в точке а равен нулю:

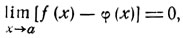
то условимся число считать корнем уравнения (1).

Это определение связано с принципом продолжения функции по непрерывности, согласно которому значение функции f(х) - φ(x) в точке а (не принадлежащей области определения) следует считать равным нулю, если ее предел в этой точке равен нулю

Примечание. Следует иметь в виду, что связанное с особыми случаями решения уравнений наивное протаскивание (характерное для старых учебников) всякого рода "раскрытия неопределенностей", "бесконечных корней" и т. п. как чего-то очевидного само по себе есть глубоко ошибочная, антинаучная точка зрения. В элементарном изложении учения об уравнениях возможно одно из двух: либо, оставаясь на базе первоначального определения, под корнем уравнения подразумевать лишь его корень в первоначальном "узком смысле" и отказаться тем самым от рассмотрения особых случаев; либо расширить понятие корня (в особых случаях) посредством точно сформулированного дополнительного определения.

Пример. Решить уравнение:

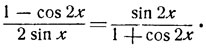
(2)

Решение. После формальных преобразований получим:

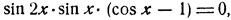
(3)

откуда

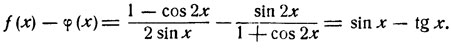
Две последние формулы решений содержатся в первой, поэтому к формула х = n^π/₂ дает общее решение уравнения (2). Переход от уравнения (2) к уравнению (3) был совершен посредством умножения обеих частей на произведение знаменателей, поэтому возможно появление посторонних решений. Подстановка х = n^π/₂ в уравнение (2) показывает, что здесь имеет место особый случай. Именно, при четном n = 2k теряет смысл левая часть, а при нечетном n = 2k+1 - правая.

Имеем ( при х≠n^π/₂):

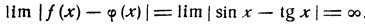
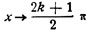
Следовательно, числа (2k+1)^π/₂ не являются корнями уравнения. При четном n имеем:

При нечетном n получим:

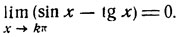
Следовательно, числа x = kπ не являются корнями в первоначальном "узком" смысле. Однако, приняв дополнительное определение, мы должны считать эти числа корнями уравнения (2).