§ 21. Различные частные приемы решения тригонометрических уравнений

Нередко можно (перенеся предварительно все члены в левую часть) разложить левую часть уравнения на множители. В этом случае уравнение распадается на несколько уравнений, получающихся поочередным приравниванием нулю сомножителей. В большинстве случаев разложение на множители левой части достигается применением формул приведения к логарифмическому виду.

Пример 1.

Решить уравнение

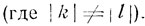
Решение. Имеем:

откуда

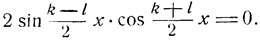
Следовательно, получаем два уравнения:

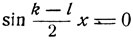
и

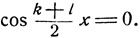
Из первого находим:

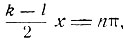
и, следовательно,

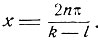
(1)

Из второго находим:

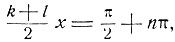
и, следовательно,

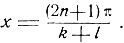
(2)

Мы получили две серии решений. Это же уравнение можно решать другим способом, рассмотренным в § 19, согласно которому имеем:

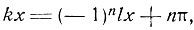
откуда

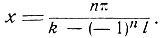
(3)

Легко видеть, что обе серии решений (1) и (2) содержатся в (3). В самом деле, если в (3) взять n четное, то получим значение х, содержащееся в (1); если взять n нечетное, то для х получим значение, содержащееся в (2). Этот пример показывает, что решение тригонометрического уравнения может оказаться представленным в различной форме в зависимости от применявшегося метода.

Пример 2.

Решить уравнение

Решение. Преобразуем левую часть:

Преобразуем правую часть:

Перенеся все члены в левую часть, перепишем данное уравнение в виде

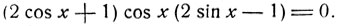
Приравнивая поочередно нулю три сомножителя, получим:

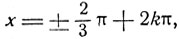
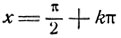
и

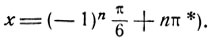
^* (Способ разложения на множители широко применяется на практике при решении уравнений различной степени трудности. Так, например, этот способ может быть применен при решении следующих номеров задачника Рыбкина: 6, 19, 20, 26, 40, 51, 52,54.)

В некоторых случаях бывает целесообразно выполнить преобразование произведения тригонометрических функций в сумму. Это преобразование осуществляется посредством формул:

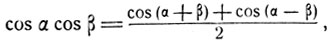
(4)

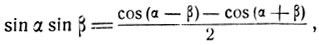
(5)

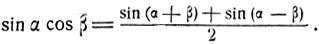
(6)

Пример 3. Решить уравнение

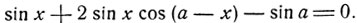
Решение. Преобразуем в сумму средний член по формуле (6).

Уравнение принимает вид:

или

откуда

и

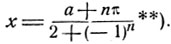
^** (Этим приемом легко решаются примеры 41 и 63 задачника Рыбкина.)

Приведем пример, когда удобно представить уравнение в виде пропорции, а затем образовать производную пропорцию и применить формулы приведения к логарифмическому виду.

Пример 4.

Решить уравнение

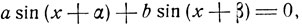
где а≠0 и b≠0, а значения α и β взяты в пределах от 0 до 2π и α≠β.

Решение. Имеем:

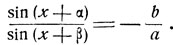
Если a≠-b, то образуем производную пропорцию

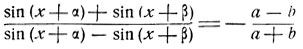
Приводя числитель и знаменатель к логарифмическому виду, получим:

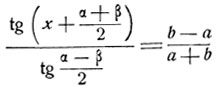
(7)

при условии ^α-β/₂≠^π/₂, т. е. α≠π+β. Из (7) находим:

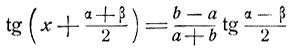
и

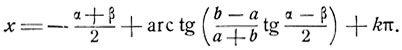
Если а = - b, то уравнение легко решается непосредственным приведением левой части к логарифмическому виду, и в составлении производной пропорции нет надобности.

Если α = β+π, то уравнение принимает вид:

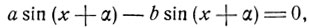
откуда при а≠b имеем sin (x + α) = 0 и x = - α + kπ.

При а = b уравнение удовлетворяется всеми значениями х^*.

^* (Составлением производной пропорции легко решается пример 43 задачника Рыбкина.)

На двух следующих примерах показан способ решения уравнения посредством введения вспомогательного угла.

Пример 5.

Решить уравнение

(где а≠0 и b≠0)).

Решение. Введем вспомогательный угол; который определим из условия

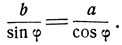
Имеем

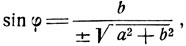
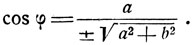
Выбрав надлежащим образом знак перед радикалом, можем считать угол φ заключенным в интервале 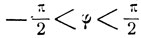(достаточно выбрать знак при условии 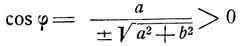tg φ = ^b/_a

и

Разделив обе части уравнения на 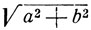(взятый с надлежащим знаком), получим:

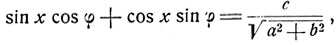
или

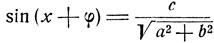
(8)

и, наконец,

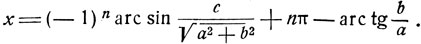
Исходное уравнение эквивалентно (8), а потому имеет решения, если

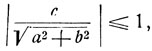
или с²≤а² + b². Если с²>а² + b², то уравнение не имеет решений.

Рассмотрим, например, уравнение

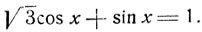
Разделив обе части на 2, положим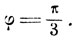

Получим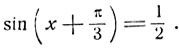

Откуда

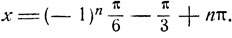
Пример 6.

Решить уравнение

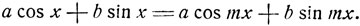
Решение. Введем вспомогательный угол 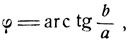получим:

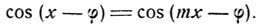
Откуда

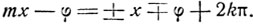
Следовательно:

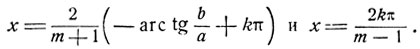
При условии, что m ≠±1. Если m = 1, то уравнение удовлетворяется тождественно. Если m = -1, то уравнение примет вид b sin х = - b sin x. Откуда при b≠0 получим sin x = 0 и х = kπ^*.

^* (Способ введения вспомогательного угла может быть применен к решению примеров 28, 30, 32, 33, 47, 53 задачника Рыбкина.)

Никакими общими правилами невозможно предусмотреть различных искусственных приемов, вносящих упрощения в процесс решения тригонометрических уравнений. Умение применять эти приемы приобретается практикой.

Пример 7.

Решить уравнение

Решение. Выделим полный квадрат из первых двух членов:

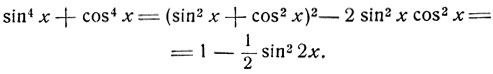
Данное уравнение примет вид:

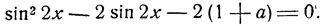
Положив t = sin 2x, получим квадратное уравнение

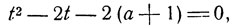
имеющее в поле комплексных чисел решения:

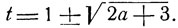
Найденные значения t действительны, если, 2а + 3≥0, откуда 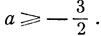Допустимые значения t определяются условием Взяв знак + перед радикалом, получим:

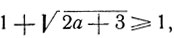
равенство имеет место лишь при условии а = -³/₂.

Рассмотрим другой корень:

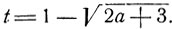
Условие 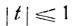выполняется, если

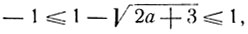
откуда

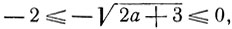
или

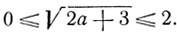
Возводя почленно в квадрат, получим:

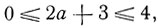
откуда

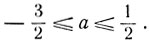
Следовательно, данное уравнение имеет решения при любом значении а, удовлетворяющем условию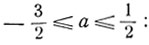

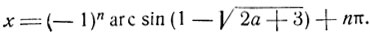
Пример 8.

Решить уравнение

Решение. Положим

имеем:

откуда

Данное уравнение примет вид:

откуда t = 1 и t = -3.

Следовательно, получаем два уравнения:

Первое уравнение было уже решено выше. Второе уравнение не имеет решений, так как каждое из слагаемых в левой части по абсолютной величине не превосходит 1 и в сумме не может получиться число - 3.