
§ 20. Рационализирующие подстановки
Рассмотрим уравнение, в котором неизвестное х содержится под знаком лишь одной тригонометрической функции. Возьмем, например, уравнение
f (sin x) = 0. (1)
Введем новое неизвестное sin x = y, тогда получим:
f (y) = 0, (2)
где допустимыми для неизвестного у следует считать значения, не превосходящие по абсолютной величине 1.
Если y1, y2, ... суть решения уравнения (2), то задача сводится к решению ряда простейших уравнений:
sin x = y1, sin x = y2, ...
Рассмотрим уравнение
2 cos 2x - 7 cos x + 3 = 0.
Решение. Полагая cos x = y получим квадратное уравнение:
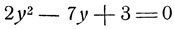
при допустимых значениях 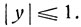 В поле действительных чисел получим два решения уравнения (3):
В поле действительных чисел получим два решения уравнения (3):
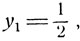
y2 = 3.
Число 3 не принадлежит множеству допустимых значений неизвестного и подлежит исключению. Итак, приходим к простейшему уравнению 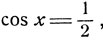 откуда:
откуда:
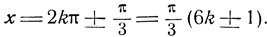
Если уравнение содержит различные тригонометрические функции от неизвестного, то можно все эти функции выразить через одну и свести задачу к решению уравнения вида (2). Однако выражения тригонометрических функций друг через друга содержат радикалы, и освобождение от них полученного уравнения может внести посторонние решения.
Рассмотрим уравнение
sin x + cos х = 1, (4)
Решение. Имеем:
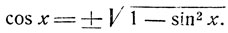
Полагая sin x = y, получим иррациональное уравнение:
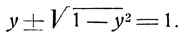
Освобождаясь от радикала, получим:
2y2 - 2y = 0,
откуда
y1 = 0, y2 = 1.
Значение y1 = sin x = 0 удовлетворяет уравнению (4) при cos x = 1. Следовательно, решению y1 = 0 соответствует положительное значение радикала. Решения уравнения (4), соответствующие корню y1 = 0, суть:
x = 2kπ,
так как из общей формулы х = nπ следует исключить нечетные значения n, дающие для косинуса значение, равное -1. Значение y2 = 1 удовлетворяет уравнению (5), откуда находим sin х = 1 или
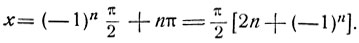
Заметим, что 2n+(-1 )n = 4k+1, будет ли n четным числом n = 2k или нечетным n = 2k+1, а потому:
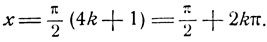
Итак, имеем две серии решений:
x = 2kπ и x = π/2+2kπ.
Мы будем изучать уравнения, являющиеся рациональными относительно входящих в них тригонометрических функций от искомого неизвестного. Предположим, что удалось выразить все функции, входящие в уравнение, через одну, причем так, что получалось уравнение рациональное относительно этой функции, которую и примем за новое неизвестное. Эта подстановка приведет к рациональному уравнению относительно нового неизвестного, а потому и называется рационализирующей подстановкой.
Решим уравнение
tg x + 3ctg x = 4.
Решение. Имеем
tg x + 3ctg x - 4 = 0.
Умножив обе части на tg x, получим:
tg2x - 4tg x + 3 = 0.
(Заметим, что значение tg x = 0 не удовлетворяет последнему уравнению.)
Подстановка z = tg x является рационализирующей. Из уравнения
z2 - 4z + 3 = 0
находим z1 = 1 и z2 = 3, откуда
x = π/4 + kπ и x = arc tg 3 + kπ.
Рассмотрим уравнение вида:
f(sin x, cos x, tg x, ctg x) = 0,
где левая часть есть рациональное выражение относительно sin х, cos x, tg x и ctg x (в частности, некоторые из тригонометрических функций могут и не входить в уравнение).
Известно, что тригонометрические функции рационально выражаются через тангенс половинного аргумента:
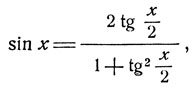
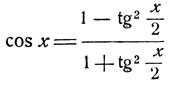
и т. д.,
а потому, приняв за новое неизвестное 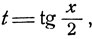 мы получим рациональное уравнение относительно t. Подстановка
мы получим рациональное уравнение относительно t. Подстановка 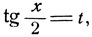 называется универсальной, так как она всегда в рассматриваемом случае приводит к рациональному алгебраическому уравнению с одним неизвестным. Так как tg x/2 теряет смысл, если х = (2k+1)π, то универсальной подстановкой можно найти все решения уравнения, кроме решений вида x = (2k+1)π (если последние существуют). Для примера рассмотрим уравнение
называется универсальной, так как она всегда в рассматриваемом случае приводит к рациональному алгебраическому уравнению с одним неизвестным. Так как tg x/2 теряет смысл, если х = (2k+1)π, то универсальной подстановкой можно найти все решения уравнения, кроме решений вида x = (2k+1)π (если последние существуют). Для примера рассмотрим уравнение
a sin х + b cos x + с = 0
(где а≠0 и b≠0).
Полагая 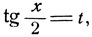 получим:
получим:
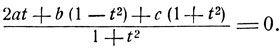
Сокращая на 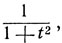 получим квадратное уравнение:
получим квадратное уравнение:
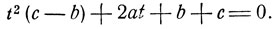
(6)
Числа вида х = (2k+1)π удовлетворяют данному уравнению, если
-b + c = 0,
поэтому исследованию подлежат два случая:
1°. b≠с. В этом случае квадратное уравнение (6) в поле комплексных чисел имеет два решения:
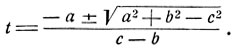
Если a2 + b2≥с2, то квадратное уравнение имеет действительные корни, и мы получим общее решение данного уравнения:
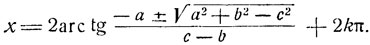
Если с2>a2 + b2, то исходное уравнение не имеет решений, так как корни уравнения (6) мнимые.
2°. b = с. В этом случае данное уравнение имеет решения вида x = (2k+1)π. Уравнение (6) обращается в уравнение 1-й степени, из которого находим вторую серию решений:
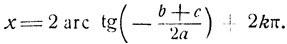
Примеры:
1) Универсальная подстановка преобразует уравнение
sin х + cos x = 1 в 2t2 - 2t = 0.
Откуда t1 = 0 и t2 = 1 и, следовательно,
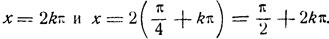
2) Решить уравнение:
cos (π sin x) = sin (π cos x).
Имеем:
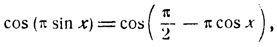
откуда
π/2 - πcos x = ±πsin x + 2kπ
или
±2sin x + 2cos x = 1 - 4k.
Мы получим уравнение вида
a sin x + b cos x + c = 0,
где a = ±2, b = 2, c = 4k - 1.
Равенство b = c, т. е. 2 = 4k - 1 не выполняется ни при каком значении k.
Общее решение данного уравнения находится по формуле (7):
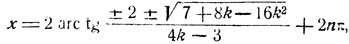
где k - любое целое число, удовлетворяющее условию:
7 + 8k - 16k2 ≥0,
а n - произвольное целое число. Следовательно, допустимые значения k суть целые числа, содержащиеся между корнями квадратного уравнения:
16k2 - 8k - 7 = 0.
Корни последнего уравнения суть k1 ≈ - 0,45 и k2 ≈ 0,95.
Следовательно, k1 = 0 есть единственное допустимое значение k.
Откуда:
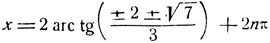
и
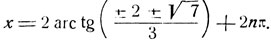
Универсальная подстановка обычно сопряжена с громоздкими вычислениями, поэтому стараются, если возможно, отыскать более простую радионализирующую подстановку*.
* (Универсальная подстановка может быть применена к примерам 30, 31, 32, 33 задачника Рыбкина.)
Если левая часть уравнения
f(sin x, cos x) = 0
есть рациональное выражение относительно sin x и cos x и содержит функцию sin x (или cos x) только в четных степенях, то можно положить f = cos х (или соответственно t = sin x), ибо четные степени синуса (или косинуса) рационально выражаются через косинус (или синус):
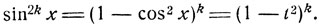
Примеры:
1. Решить уравнение
3 - 7 cos 2х sin x - 3 sin3 x = 0.
Решение. Положим sin x = t и заменим cos2 x на 1-t2, тогда получим кубическое уравнение:
4t3 - 7t + 3 = 0.
Последнее уравнение имеет три действительные корня:
t1 = 1, t2 = 1/2 и t3 = -3/2,
откуда
x = π/2 + kπ
и
x = (-1)nπ/6 + nπ.π
2. Решить уравнение
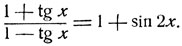
Решение. В данном случае для рационализации достаточно положить tg x = t, так как
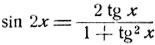
рационально выражается через t. Имеем:
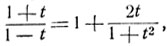
откуда:
2(1+t)t2 = 0.
Из последнего уравнения находим два различные решения:
t = -1 и t = 0,
откуда
x = - π/4+kπ и x = kπ.
3. Решить уравнение
5 cos 2х = 4 sin х.
Решение. Так как cos 2x выражается рационально через sin x:
cos 2х = cos2 x - sin2 х = 1 - 2 sin2 x, то
для рационализации достаточно положить t = sin x, тогда получим:
5 - 10t2 = 4t
или
10t2 + 4t - 5 = 0,
откуда
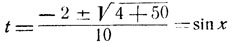
и
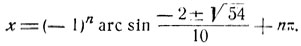
Рассмотрим уравнение вида
f(sin х, cos x) = 0,
в котором левая часть есть однородный многочлен (т. е. многочлен, все члены которого имеют одинаковую степень) относительно sin x и cos x. При решении однородных уравнений применяется подстановка tg x = t. Рассмотрим, например, однородное уравнение 3-й степени:
sin3 х - sin2 x cos x - 3 sin x cos2 x + 3 cos3 x = 0.
Заметим, что при cos x = 0 уравнение не удовлетворяется*.
* (Если положить cos x = 0, то получим sin3 х = 0, и, следовательно, sin x = 0, но равенства sin x = cos х = 0 не могут выполняться ни при каком значении х. Если бы в уравнении не содержался член с sin3 x, то можно было бы предварительно вынести общий множитель, равный cos x, и приравнять его отдельно нулю. )
Разделив обе части на cos3 х, получим:
tg3 х - tg2 x - 3tg x + 3 = 0.
Полагая tg x = t, получим кубическое уравнение:
t3 - t2 - 3t + 3 = 0,
имеющее корни
t = 1, и t = ±√3,
откуда
x = π/4 + kπ и x = ±π/3 + kπ*
* (Различные рационализирующие подстановки могут быть применены к решению, например, следующих номеров § 14 задачника Рыбкина: 3, 16, 24, 34, 42, 46, 48, 49, 50, 59. )
Ниже даны примеры уравнений, приводящихся к однородным:
1° a sin2x + b sin x cos х + c cos2 x = d.
Достаточно правую часть заменить на d(sin2 x + cos2 х), чтобы получить однородное уравнение 2-й степени.
2° a sin4 х + b sin3 x cos x + c cos3 x sin x = d.
Достаточно правую часть заменить на d(sin2 x + cos2 x)2, чтобы получить однородное уравнение 4-й степени.
3° a sin2 х + b sin 2x + с cos 2х + d cos2 х = e.
Достаточно преобразовать sin 2х и cos 2х по известным формулам и заменить e на e (sin2 x + cos2 x), чтобы получить однородное уравнение 2-й степени.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'