§ 19. Соотношения между двумя дугами, имеющими одинаковое значение данной тригонометрической функции

Теорема. Необходимым и достаточным условием того, чтобы

1° две дуги u и v имели одинаковый синус:

является наличие соотношения

2° чтобы дуги u и v имели одинаковый косинус:

является наличие соотношения

3° чтобы дуги и и v имели одинаковый тангенс (или котангенс), является наличие соотношения

где n - некоторое целое число.

Доказательство. Докажем утверждение 1°.

Условие достаточное. В самом деле, если имеет место соотношение u = (-1)ⁿv + nπ, то в зависимости от четности или нечетности n имеем:

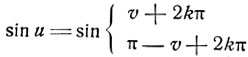
в обоих случаях sin u = sin v.

Условие необходимое. Пусть sin u = sin v; обозначим через m общее значение синуса двух дуг u и v:

Рассмотрим множество всех дуг, имеющих синус, равный m:

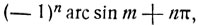
(1)

каждая из дуг u и v содержится в выражении (1) при некотором значении n:

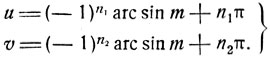
(2)

Если числа n₁ и n₂ одинаковой четности (т. е. оба четные или нечетные), то вычтем почленно равенства (2):

где n₁ - n₂ есть некоторое четное число 2k. Если n₁ и n₂ - числа различной четности, то сложим почленно (2):

где n₁ + n₂ - есть некоторое нечетное число 2k+1. Итак, если дуги u и v имеют одинаковое значение синуса, то либо их разность равна целому числу периодов 2лπ, либо их сумма равна нечетному числу полупериодов (2k+1)π. Следовательно,

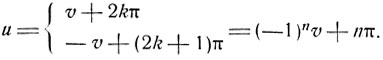
Рассуждения в случаях 2° и 3° аналогичны. Так, в случае 2° при наличии соотношения

имеем

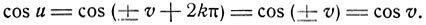
Обратно, если,

то

Складывая или вычитая (в зависимости от знаков при arc cos m в правых частях), получим:

где n = n₁±n₂ - целое число^*.

^* (Теореме можно дать другое доказательство. Так, в случае 1° имеем:

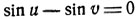
или

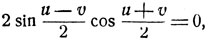
откуда (необходимое и достаточное условие)

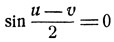
или

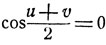
и, следовательно,

u - v = 2kπ или u + v = (2k+1)π,

откуда, объединяя формулы в одну, придем к тому же окончательному результату.)

Доказанная теорема применяется, когда уравнение представлено в виде равенства некоторой тригонометрической функции от двух выражений, содержащих неизвестное. Пусть, например, дано уравнение

(вместо синуса можно взять любую другую тригонометрическую функцию). На основании доказанной теоремы равенство (3) равносильно уравнению

с целочисленным параметром n.

Примеры:

1.

Решение. Имеем:

откуда

(4)

(знаки берутся либо верхние, либо нижние).

Если 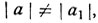то

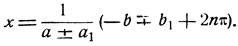
Теперь рассмотрим случай, когда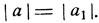

Пусть, например, а = a₁ тогда, взяв в левой части равенства (4) знак + перед а₁ получим:

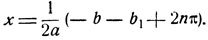
Если взять верхние знаки, то получим:

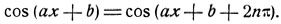
Последнее соотношение противоречиво и не дает решений, если разность b₁ - b не равна целому числу периодов; если же b₁ = b + 2nπ, то при а = а₁ данное уравнение обращается в тождество:

Пусть, например, дано уравнение

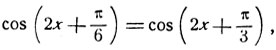
имеем:

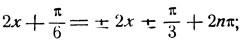
выбор верхних знаков дает противоречивое соотношение:

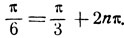
Выбор нижних знаков дает решения:

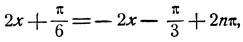
откуда

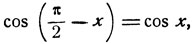
2. Решить уравнение sin x = cos x.

Решение. Имеем:

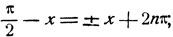
откуда

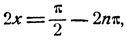
(5)

выбрав в правой части знак +, получим:

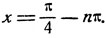
откуда х = ^π/₄ - nπ. Заметив, что коэффициент - n можно заменить на n (ибо -n, равно как и n, может иметь произвольные целые значения), получим серию решений:

Выбор знака минус в правой части (5) приводит к противоречивому соотношению.

3. Решить уравнение

Решение:

или

откуда

и, следовательно,

4. Решить уравнение

Решение. Имеем tg 5х = tg (- 2x), следовательно:

откуда

^* (Указанным в настоящем параграфе способом могут быть решены примеры 4, 18, 19, 55, 57 § 14 задачника Рыбкина.)