§ 18. Простейшие тригонометрические уравнения

Простейшими тригонометрическими уравнениями будем называть уравнения:

Решение простейшего тригонометрического уравнения заключается в отыскании множества всех дуг, имеющих заданное значение рассматриваемой тригонометрической функции. Для нахождения множества всех дуг по известному численному значению тригонометрической функции достаточно (в силу периодичности тригонометрических функций) найти все дуги, лежащие в пределах одного периода (т. е. на любом сегменте, величина которого равна периоду) и имеющие данное значение тригонометрической функции. Прибавляя к каждой из найденных дуг любое целое число периодов, мы и получим искомое общее решение данного простейшего уравнения. Перейдем к рассмотрению простейших уравнений.

1°. sin x = m, где m - данное действительное число. При 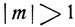уравнение не имеет решений, так как абсолютная величина синуса не может быть больше 1. Предположим, что 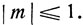На сегменте 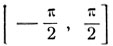содержится единственная (в силу монотонности синуса) дуга х₁ = arc sin m, синус которой равен m. На сегменте 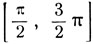содержится единственная (в силу монотонности) дуга x₂ = π-arc sin m, синус которой равен m. Но оба сегмента 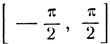и 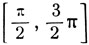охватывают полный период синуса, поэтому, чтобы получить общее решение данного уравнения, достаточно к каждой из дуг х₁ и х₂ прибавить любое целое число периодов синуса:

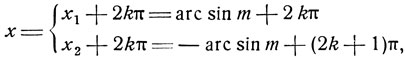
где k - любое целое число (положительное, отрицательное или 0). Полученное выражение можно записать в виде одной формулы, заметив, что в верхней строке, arc sin m + 2kπ, слагаемое arc sin m берется со своим знаком и коэффициент при π - четное число 2k; в нижней строке arc sin m берется с обратным знаком, а коэффициент при π есть нечетное число 2k+1.

Выражение

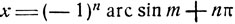
дает при четном n = 2k верхнюю строку, а при нечетном n = 2k+1 нижнюю строку.

На чертеже 45 дано графическое пояснение множественности решений уравнения sin x = m.

Черт. 45

Примеры:

1) Найти множество всех дуг, синус которых равен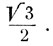

Имеем:

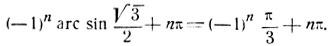
На чертеже 46 стрелками показаны различные дуги, которые мы получим, придавая в формуле числу n различные целочисленные значения.

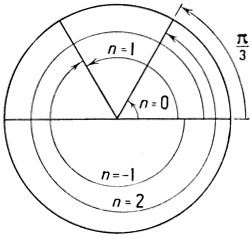
Черт. 46

2) Найти множество всех дуг, синус которых равен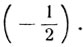

Имеем:

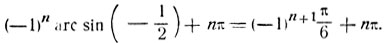
(Чертеж 47.)

Черт. 47

2°. cos x = m. Если 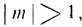то уравнение не имеет решений. Если 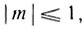то на сегменте 0≤x≤π уравнение имеет единственное решение х = arc cos m. Дуга - arc cos m также является решением данного уравнения. Эта дуга расположена на сегменте -π≤х≤0. Таким образом, дуги х₁ = arc cos m и х₂ = -arc cos m суть два решения данного уравнения, заключающиеся на сегменте от -π до π. Так как этот сегмент охватывает полный период косинуса, то множество всех искомых дуг найдем, прибавляя к хх и х2 любое целое число полных окружностей:

Объединяя оба выражения в одно, запишем:

Примеры:

1. Решить уравнение cos х = -¹/₂.

Решение. х = ± arc cos (-¹/₂) + 2kπ = ±^2π/₃ + 2kπ.

2. Решить уравнение cos x = 0.

Решение. х = ±arc cos 0 + 2kπ = ±^π/₂ + 2kπ = (n + ¹/₂)π (где n - любое целое число)^*.

^* ( Заметим, что ±¹/₂ + 2k = ^4k±1/₂, но 4k ± 1 изображает произвольное нечетное число: 4k ± 1 = 2n + 1, где n - любое целое число.)

3) Решить уравнение cos х = ¹/_√2.

Решение. Имеем

3°. tg x = m. При любом действительном m уравнение имеет в интервале -^π/₂<x<^π/₂ единственное решение. Этот промежуток охватывает полный период тангенса, а потому множество всех дуг, имеющих значение тангенса, равное m, запишется формулой:

Множественность решений уравнения tg x = m пояснена графически на чертеже 48.

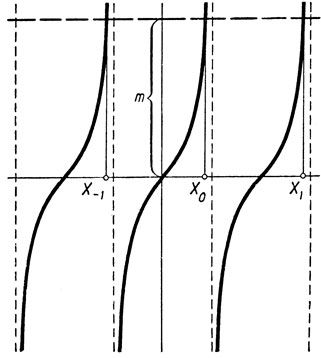
Черт. 48

Пример:

Решить уравнение tg x = - 1.

Решение. x = arс tg (-1) + kπ = - ^π/₄ + kπ.

4°. ctg x = m. При любом действительном m уравнение имеет единственное решение в промежутке 0<x<π:

Общее решение данного уравнения:

Решение уравнений, непосредственно приводящихся к простейшим, поясним на нижеследующих примерах^*.

^* (Непосредственно приводящимися к простейшим являются уравнения, данные в примерах 9, 10, 11, 12 и 14 § 14 задачника Рыбкина.)

Примеры:

1. sin 3x = ¹/₂.

Решение.

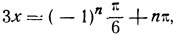
откуда

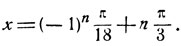
2.

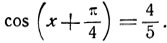
Решение.

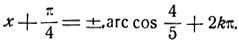
Откуда

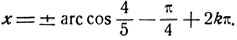
Величину arc cos ⁴/₅ можно найти приближенно по таблицам.

Имеем (в градусной мере) arc cos ⁴/₅≈ 36°52'.

Следовательно,

3. tg (ax + b) = m.

Решение.

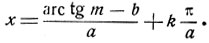
4. sin х² = -¹/₂.

Решение.

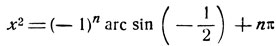
или

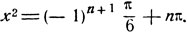
Условие х²≤0 показывает, что допустимыми значениями n следует считать лишь те целые значения, при которых

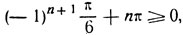
откуда n = 1, 2, 3, ... (значения 0, -1, -2, ... не являются допустимыми для n). Итак, имеем:

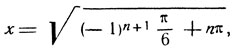
где n - произвольное натуральное число.