Дополнение II. Аркфункции от комплексного аргумента

Мы рассматривали аркфункции как функции, обратные тригонометрическим, причем тригонометрические функции считались определенными только для действительных значений аргумента. Из курса математического анализа известно, что тригонометрические функции могут быть определены для произвольного комплексного значения аргумента при помощи следующих степенных рядов, сходящихся при произвольных комплексных значениях аргумента:

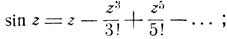
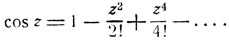
Полагая в ряде, определяющем показательную функцию:

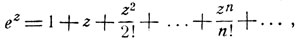
z = ±ix мы получим известные формулы Эйлера:

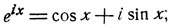
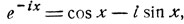
откуда можно выразить тригонометрические функции через показательные следующим образом:

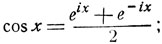
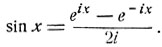
Перейдем теперь к обратным тригонометрическим функциям. Рассмотрим функцию y = sin x. В силу формул Эйлера

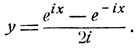
Выразим теперь х через у:,

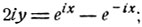
и

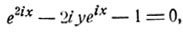
откуда:

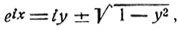
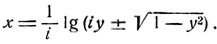
Таким образом, функция, обратная тригонометрической функции sin x, выражается при помощи логарифма. Логарифм комплексного числа имеет бесконечное множество значений и поэтому функция:

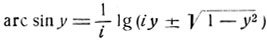
является бесконечнозначной функцией. Эта функция определена при всех значениях y (не только для значений |y|≤1), так как iy+√(1-y²) не обращается в нуль ни при каком значении y (в самом деле, освобождая уравнение iy ± √(1-y²) = 0 от радикала, мы получим 1 = 0).

При действительных значениях y, удовлетворяющих неравенствам -1≤y≤1, значения arc sin y действительны.

В самом деле:

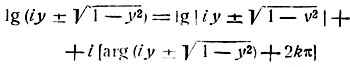
(под символом arg z мы понимаем одно из значений аргумента комплексного числа z). Но если -1≤y≤1, то √(1-y²) есть число действительное, и следовательно:

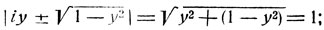
отсюда следует:

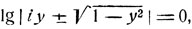
откуда:

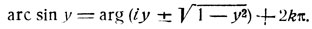
Отсюда видно, что значения функции arc sin y действительны, если -1≤y≤1. В самом деле, полагая arg(iy ± √(1-y²) = φ легко видеть, что определяется из условий sin φ = ±iy; cos φ = ±√(1-y²), так как

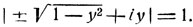
При выборе перед радикалом знака плюс в качестве значения φ можно взять φ = arc sin y, где arc sin y есть функция действительного аргумента, уже определенная в главе II. При выборе знака минус перед радикалом мы можем положить φ = π - arc sin y.

Рассмотрим функцию:

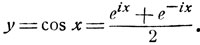
Отсюда

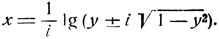
функция, обратная функции y = cos x, есть:

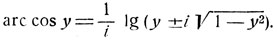
Полученная функция бесконечнозначная и определена для всех значений у. Как легко убедиться, значения arc cos y действительны, если -1≤y≤1 (доказательство предоставляем провести читателю).

Рассмотрим теперь функцию y = tg x; так как

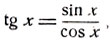
то

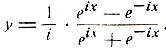
Из последнего равенства найдем:

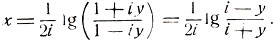
Бесконечнозначная функция:

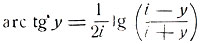
определена для любого значения y≠±i. При y = ±i эта функция теряет смысл, так как при этих значениях выражение, стоящее под знаком логарифма, обращается соответственно в нуль и бесконечность. Для любого действительного значения y имеем:

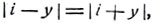
откуда:

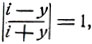
а следовательно, как легко видеть, значения arc tg y, соответствующие действительным значениям y, будут также действительны.