
§ 16. Примеры
1) Полагая в формулах (1), (3), (5) y = х, получим:
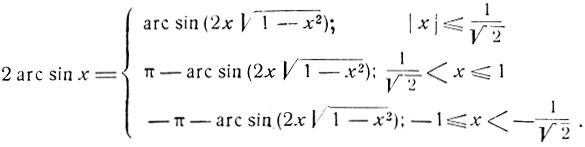
(7)
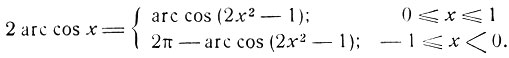
(8)
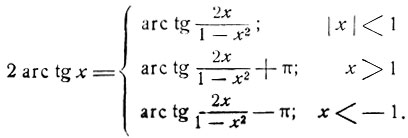
(9)
2) Исследовать функцию 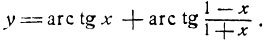
Рассмотрим второе слагаемое. Полагая в формуле (6)
х = 1, а y = х,
получим
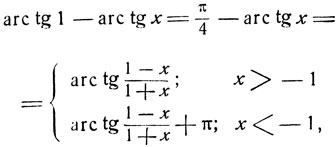
откуда
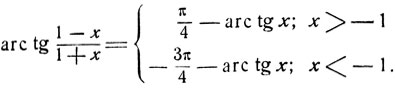
Следовательно,
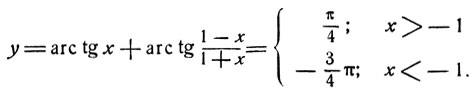
Данная функция является разрывной, ее график состоит из двух прямых, параллельных оси абсцисс (черт. 37).
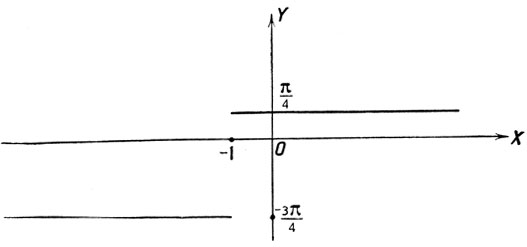
Черт. 37
3) Исследовать функцию
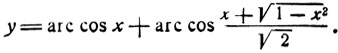
Полагая в формуле (4) 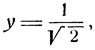 получим:
получим:
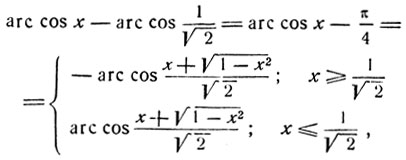
откуда
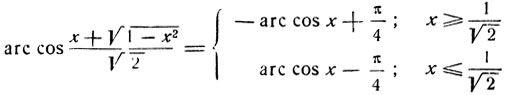
следовательно,
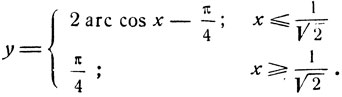
Построим график данной функции. Сегмент [-1, 1], на котором определена функция, разобьем на два сегмента 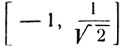 и
и 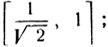 на первом сегменте
на первом сегменте
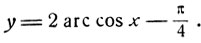
Следовательно, y убывает от -7π/4 до π/4. На втором сегменте 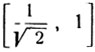 y имеет значение, равное π/4 (черт. 38).
y имеет значение, равное π/4 (черт. 38).
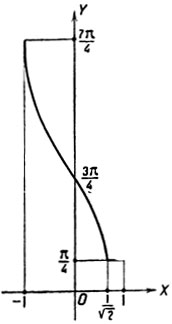
Черт. 38
4) Исследовать функцию
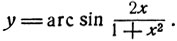
Установим область определения. Эта функция определена для всех значений аргумента хж так как при любом значении х имеет место неравенство: 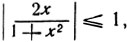 или, что то же
или, что то же 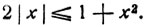
В самом деле, принимая во внимание, что при всех значениях х, 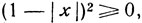 имеем
имеем 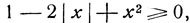 откуда
откуда 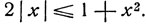 Воспользуемся формулой (стр. 38):
Воспользуемся формулой (стр. 38):
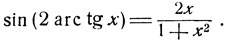
Рассмотрим две дуги 2 arc tg x и 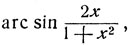 имеющие одинаковый синус. Для дуги 2 arc tg x имеют место неравенства -π< 2 arc tg x<π; для второй дуги имеем
имеющие одинаковый синус. Для дуги 2 arc tg x имеют место неравенства -π< 2 arc tg x<π; для второй дуги имеем
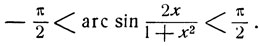
Если значение х заключено на сегменте [-1, 1], то:
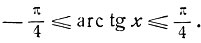
Следовательно,
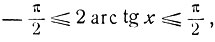
и мы имеем:
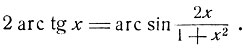
Для значений x<-1 имеем -π< 2arc tg x<-π/2, а потому:
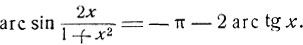
Черт. 39
Если x>1, то,
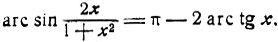
Черт. 40
Итак, получим:
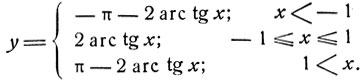
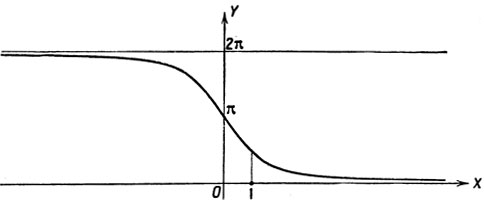
Черт. 41
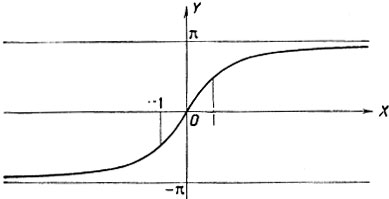
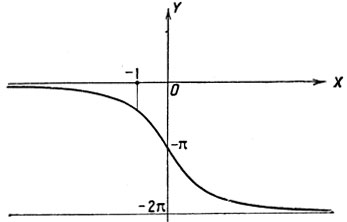
Построим графики функций 2 arc tg x (черт. 39), -π - 2 arc tg x (черт. 40) и π - 2 arc tg x (черт. 41). График данной функции получается путем соединения трех дуг построенных линий, как это показано на чертеже 42.
Черт. 42
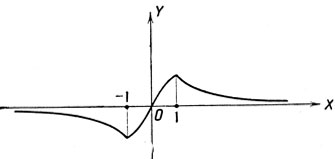
5) Исследовать функцию
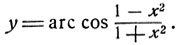
Так как при любом значении х
1-x2≤1+x2,
то данная функция имеет смысл при всех значениях х.
Воспользуемся формулой (стр. 38):
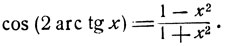
Рассмотрим две дуги, имеющие одинаковый косинус:
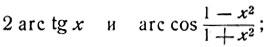
в силу определения аркфункций имеем:
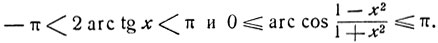
Откуда:
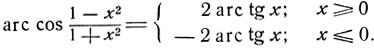
На чертеже 43 изображен график этой функции.
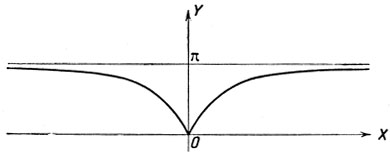
Черт. 43
6) Исследовать функцию:
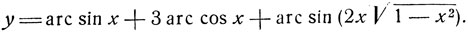
Согласно формуле (7) (стр. 61):
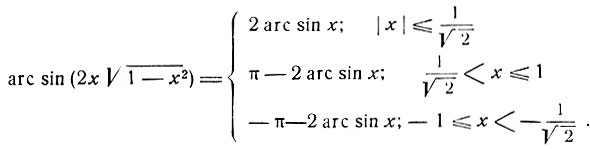
Принимая во внимание, что 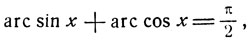 получим:
получим:
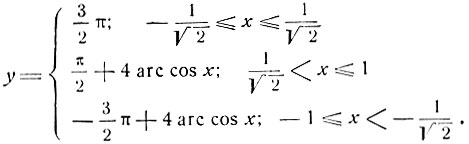
График этой функции изображен на чертеже 44.
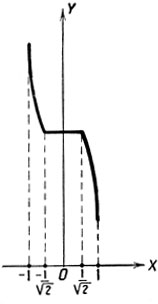
Черт. 44
7) Преобразовать в арксинус дугу arc sin x + arc tg y. На основании формулы (стр. 46) данную дугу можно представить в виде суммы арксинусов следующим образом:
Теперь остается применить формулу (1). Предоставляем читателю докончить вычисления.
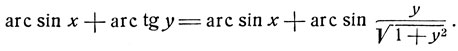
Упражнения.
- Вычислить:
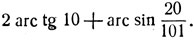
- Вычислить:
[применить два раза формулу (9)]
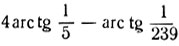
- Доказать справедливость равенств:
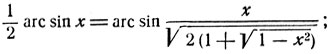
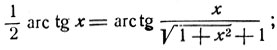
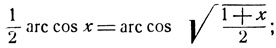
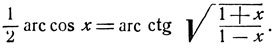
- На основании предыдущего примера доказать равенство:
Указание: принять во внимание равенство
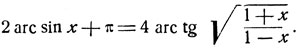
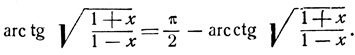
- Исследовать функцию
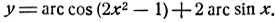
- Исследовать функцию:
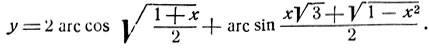
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'