Глава V. Теоремы сложения

§ 15. Основные формулы

Теоремы сложения тригонометрических функций дают выражения тригонометрических функций суммы через тригонометрические функции слагаемых. Применительно к аркфункциям эти теоремы дают возможность представить сумму двух или нескольких аркфункции при помощи любой из аркфункции. Поясним сказанное на частных примерах.

1) Рассмотрим сумму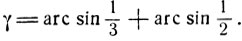

Эта сумма является суммой двух дуг α и β, где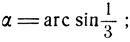

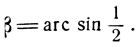
Зная дуги α и β, можно вычислить значение любой тригонометрической функции дуги γ = α+β и, следовательно, представить дугу γ при помощи любой из аркфункции. Заметим, что в данном случае α<^π/₄(¹/₃<¹/_√2, а следовательно, arc sin ¹/₃ <^π/₃, а также 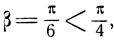поэтому 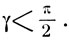Вычисляя синус дуги γ, будем иметь:

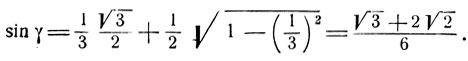
Так как сумма γ заключена на сегменте 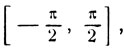то

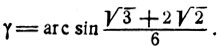
Ясно, что можно рассматривать любую другую тригонометрическую функцию дуги γ и представить эту дугу при помощи соответствующей аркфункции. Так, например,

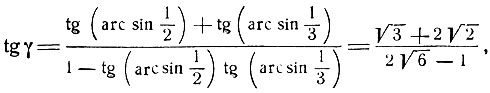
откуда:

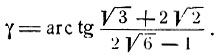
2) Положим γ = arc tg 1 + arc tg 2; пусть α = arc tg 1; β = arc tg 2. В этом случае, в отличие от предыдущего, γ>^π/₂, так как α = ^π/₄ и β > ^π/₄.

Таким образом, дуга γ заключена в интервале 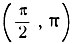Рассмотрим tg γ:

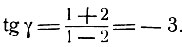
Однако в данном примере нельзя написать γ = arc tg (-3), так как дуги y и arc tg (-3) заключены в различных интервалах:

В данном случае мы будем иметь:

Вычислим cos γ:

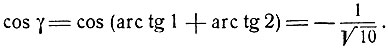
Принимая во внимание, что дуги γ и arc cos 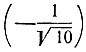расположены в одном и том же интервале (0, π) и имеют одинаковый косинус, получим:

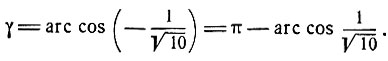
Перейдем к изучению в общем виде преобразований суммы аркфункции. Рассмотрим ряд наиболее часто встречающихся случаев.

Рассмотрим сумму γ = arc sin x + arc sin y

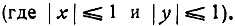
Вычисляя sin γ, найдем:

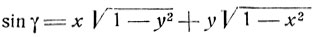
(см. §12).

Отсюда еще нельзя заключить, что

Дело в том, что дуги arc sin x + arc sin y = γ и

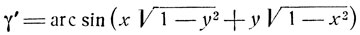
могут оказаться расположенными в различных промежутках. 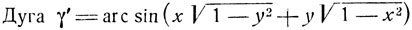при всех значениях х и н заключена на сегменте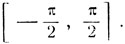

Для значения дуги γ возможны следующие три случая.

Случай I:

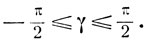
Если числа х и y разных знаков или хотя бы одно из них равно нулю, то имеет место случай I.

Так, при 0≤x<1 и -1≤y≤0 имеем:

откуда:

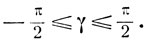
Если при x>0, y>0 имеет место случай I, то

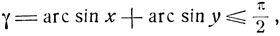
откуда:

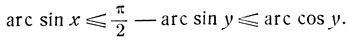
Следовательно (в силу возрастания синуса в первой четверти),

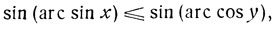
или:

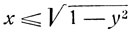
и

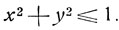
Аналогично покажем, что если при х<0, y<0 имеет место случай 1, то

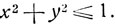
Случай II:

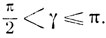
В этом случае х>0, y>0 и

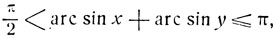
откуда

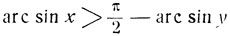
и (взяв синус от обеих частей) х²+y²>1.

Случай III:

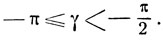
Этот случай имеет место при х<0, y<0 и

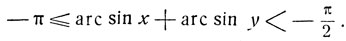
Изменив знаки на противоположные, приходим к предыдущему случаю: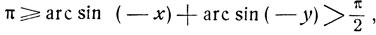

откуда

Из сопоставления результатов следует, что признаком случая I при одинаковых по знаку значениях аргументов (т. е. при хy>0) может служить неравенство х²+y²≤1. Случай II имеет место, если х>0, y>0 и х²+y²>1. Случай III имеет место, если х<0, y<0 и х²+y²>1.

Дуги 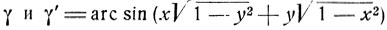имеют одинаковый синус, но (по определению арксинуса) 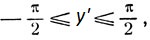следовательно, в случае I, γ = γ'; в случае II γ = π - γ' и в случае III γ = -π - γ'.

Итак, имеем окончательно:

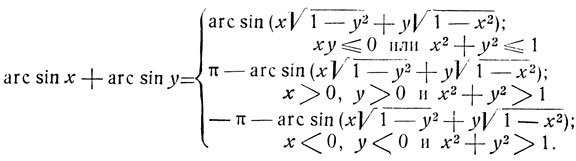
Пример:

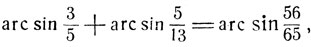
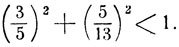
Из формулы (1) можно получить формулу преобразования разности arc sin x - arc sin y. В самом деле, эту разность можно представить в виде суммы:

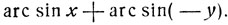
Заменяя в формуле (1) y на -y, получим:

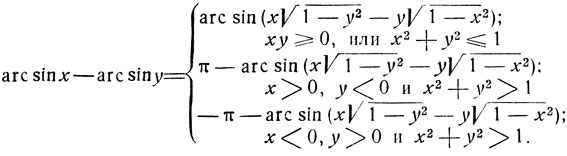
Сумму arc sin x + arc sin y можно представить при помощи любой другой аркфункции. Так, например, приняв во внимание равенство

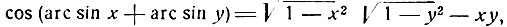
рассмотрим две дуги:

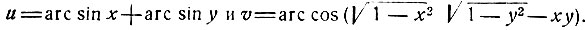
Ясно, что u = cos v.

Рассмотрим случай, когда аргументы суть числа одинаковых знаков: хy>0.

Мы знаем, что -π<u<π; 0<v<π. Легко видеть, что 0≤u≤π, если х≥; y≥0 и -π<u≤0, если х<; y<0, поэтому

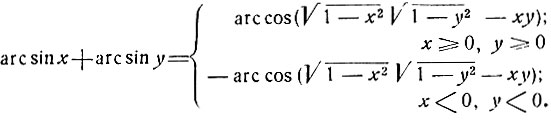
Мы рассмотрели преобразование суммы arc sin x + arc sin y в арккосинус для случая, когда x и y являются числами одинакового знака. Случай, когда х и y суть числа разных знаков, может быть сведен к рассмотрению разности

но тогда (как легко проверить)

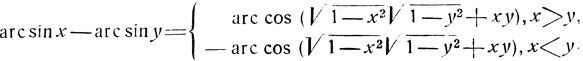
В качестве упражнения рекомендуем проверить справедливость следующей формулы:

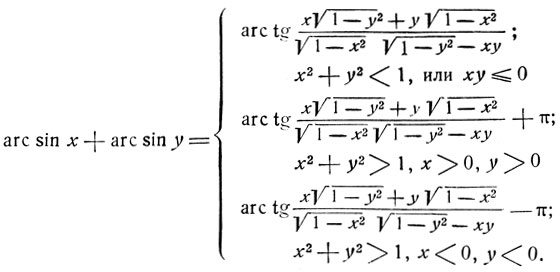
Рассмотрим сумму arc cos x + arc cos y. В силу основных неравенств

имеем:

Выведем признак, по которому можно судить, на каком из сегментов [0, π] или [π, 2π] расположена дуга

Если

то

Принимая во внимание, что обе дуги arc cos x и π - arc cos y расположены в промежутке [0, π] и что на этом промежутке косинус убывает, будем иметь:

и, следовательно, х≥-y, откуда х+y≥0.

Если выполнены неравенства π≤ arc cos х + arc cos y≤2π, то π - arc cos y≤arc cos x, откуда при помощи рассуждений, аналогичных предыдущим, получим х+y≤0. Отсюда в частности получим, что дуга arc cos x + arc cos y расположена на сегменте [0, π], если x>0 и y>0, и на сегменте [π, 2π], если х<0 и y<0.

Резюмируя полученные результаты, приходим к следующему выводу:

если

если

Из равенства:

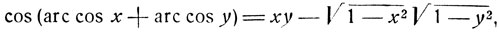
следует, что дуги:

u = arc cos x + arc cos y и 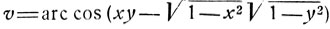имеют одинаковый косинус.

Если 0&38804;u≤π, то u = v; если же π≤u≤2π, то u = 2π-v, следовательно, имеем формулу:

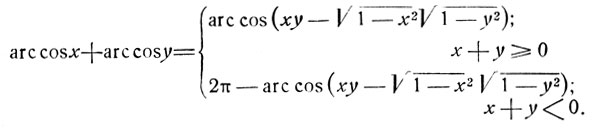
Заменяя y на -y и принимая во внимание, что

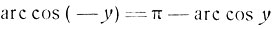
и

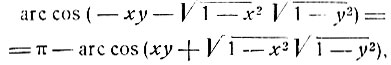
получим:

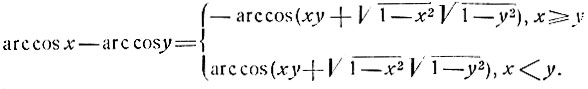
Пример:

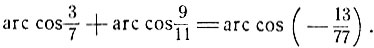
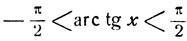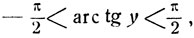Рассмотрим сумму arc tg x + arc tg y. Исследуем, в каких промежутках может быть заключена эта сумма при различных значениях х и y. В силу неравенств и имеем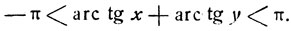

Дальнейшие рассуждения аналогичны соответствующим рассуждениям, относящимся к сумме арксинусов, поэтому мы не будем останавливаться на подробностях.

Если х и у суть числа разных знаков, то

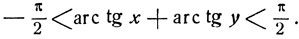
Если х≥0 и y≥0, то 0≤arc tg х + arc tg y<π. Установим, в каком из промежутков 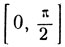или 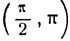расположена рассматриваемая сумма. Если

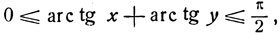
то

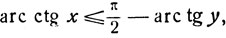
и, следовательно,

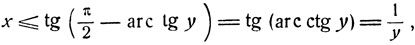
откуда 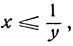а значит xy≤1. Подобным же образом легко показать, что если 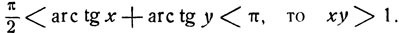Аналогично покажем, что в случае х<0 и y<0 сумма arc tg x + arc tg y расположена в промежутке 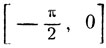или 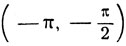в зависимости от того, которое из двух неравенств ху<1 или хy>1 имеет место. Равенство ху = 1 имеет место, если

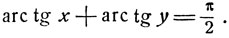
Итак, дуга y = arc tg x + arc tg y заключена в интервале 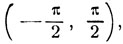если x и y - числа разных знаков (ху≤), а также, если х и у, будучи числами одинаковых знаков, удовлетворяют условию ху<1. Эти оба условия можно объединить в одно: ху<1. Дуга γ заключена в интервале 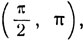если х>0 и y>0 и ху>1. Это условие можно записать так: x>0 и ху>1, ибо из последних двух неравенств само собой следует неравенство y>0. Ясно, что это же условие можно также записать в виде неравенств y>0, ху>.

Наконец, дуга arc tg x + arc tg y заключена в интервале (-π, -^π/₂) при условии х<0, ху>1. Это условие равносильно неравенствам у<0, ху>1.

Выведем формулу преобразования суммы арктангенсов в арктангенс.

Рассмотрим равенство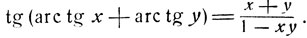

Полагая u = arc tg x + arc tg y и 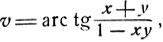имеем tg v = tg u. Так как 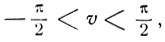то u = v, если 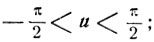u = π+v, если ^π/₂<u<π, и, наконец, u = -π+v, если -π<u<-^π/₂, поэтому:

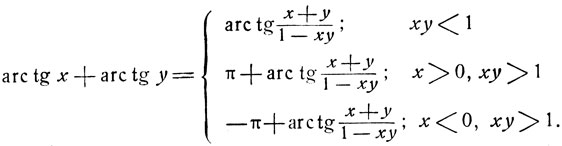
Если хy = 1, то выражение 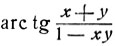не имеет смысла, в этом случае дуга

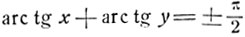
не имеет тангенса и не может быть представлена в виде арктангенса.

Заменяя y на -y, получим:

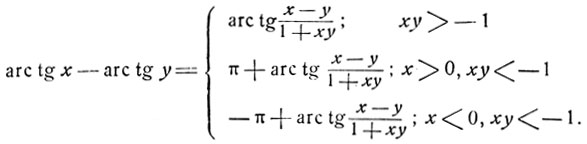
Пример:

В данном примере 3*¹/₂>1.

Выведенными формулами не ограничиваются возможные преобразования суммы аркфункций. Не обязательно рассматривать сумму или разность одноименных аркфункций. Так, например, можно вывести формулы преобразования суммы arc sin x + arc tg y в любую другую аркфункцию. Можно было бы рассмотреть формулы преобразования суммы большего числа, чем двух аркфункций. Не будем продолжать рассмотрения этих преобразований, полагая, что приемы их выполнения достаточно выяснены на рассмотренных примерах.

Примечание. При решении числовых примеров, следует стараться избегать пользования громоздкими и трудно запоминаемыми общими формулами, а всякий раз руководствоваться конкретными числовыми данными.

Пример (сб. задач Рыбкина, § 15, № 31).

Показать, что

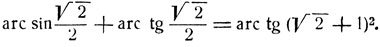
Имеем:

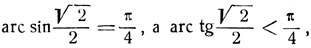
ибо 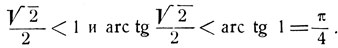Следовательно, сумма дуг в правой части доказываемого равенства заключена в 1 четверти. Взяв тангенс от левой части, получим

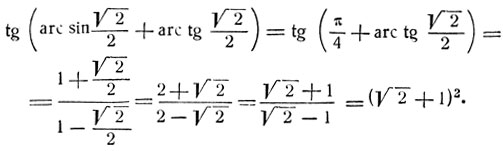
Откуда следует доказываемое равенство.

Непосредственное выполнение исследования (без пользования готовыми формулами) может успешно применяться и при преобразовании суммы аркфунций с буквенными аргументами.

Пример:

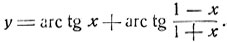
Имеем:

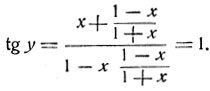
Так как -π<y<π, то y = ^π/₄ либо y = -^3π/₄. Равенство y = -^3π/₄ может иметь место лишь при условии, если выражения, находящиеся под знаками обоих арктангенсов, отрицательны:

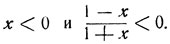
Эта система неравенств удовлетворяется, если х<-1.

Итак, имеем:

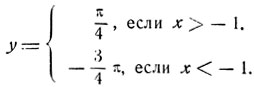
(другое решение этого примера дано в § 16, см. пример 2).