
§ 14. Соотношения второго рода
Соотношения второго рода между аркфункциями вытекают из соотношений, имеющих место между значениями тригонометрических функций от одного и того же аргумента.
Рассмотрим сначала несколько частных примеров.
1) Мы знаем, что
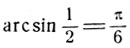
и
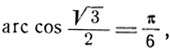
следовательно,
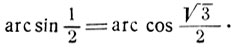
Из этого примера мы видим, что данная дуга может быть представлена как арксинус и как арккосинус различных аргументов.
2) Дело изменится, если мы пожелаем представить в виде арккосинуса дугу
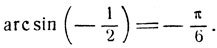
В самом деле, arc cos x не может иметь отрицательных значений (0≤arc cos x≤π) и поэтому ни при каком значении х не может иметь место равенство
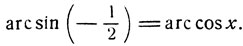
Выразить дугу 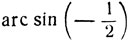 через арккосинус можно так: принимая во внимание равенства
через арккосинус можно так: принимая во внимание равенства
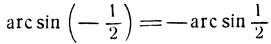
и
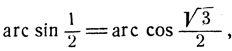
получим:
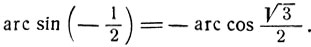
3) 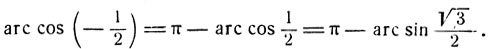
Перейдем к рассмотрению в общем виде вопроса о преобразовании одной аркфункции в другую. Рассмотрим сначала какую-нибудь пару аркфункции, значения которых заключены в одних и тех же пределах. Для определенности возьмем arc sin x и arc tg x. Значения обеих этих функций заключены в промежутке от -π/2 до π/2, в этом промежутке дуга вполне определена, если задано значение ее тангенса или синуса. Пусть y = arc sin x, тогда
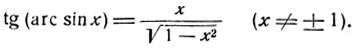
(1)
Дуга 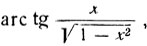 по определению арктангенса, имеет тангенс, равный
по определению арктангенса, имеет тангенс, равный 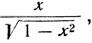 и расположена в интервале
и расположена в интервале 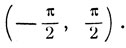
В силу (1) дуга arc sin x имеет тот же тангенс и расположена в том же интервале 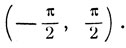 Откуда получаем соотношение
Откуда получаем соотношение
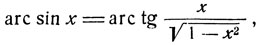
(2)
справедливое при всех значениях x, по абсолютной величине меньших единицы [если |х|≥1, то выражения, стоящие в правой и левой частях равенства (2) теряют смысл]. Соотношение (2) является следствием формулы элементарной тригонометрии, выражающей тангенс через синус.
Подобным же образом из равенства:
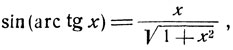
вытекает соотношение:
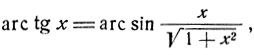
(3)
справедливое при всех действительных значениях x.
Аналогичным образом обстоит дело с преобразованием арккосинуса в арккотангенс. В пределах (0, π) дуга вполне определяется заданием значения косинуса или котангенса, поэтому из равенств:
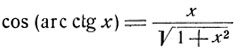
и
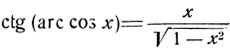
следуют соотношения:
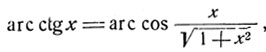
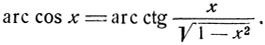
(4)
Положение дела меняется, если мы попытаемся преобразовать одну в другую аркфункции, значения которых содержатся в различных промежутках.
Рассмотрим функцию y = arc sin x и попытаемся преобразовать ее в арккосинус. Для значений 0≤x≤1 имеем:
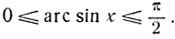
Дуга y имеет косинус, равный 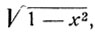 и поэтому
и поэтому
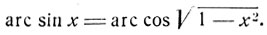
Если
-1≤x≤0, то -π/2≤arc sin x≤0,
для функции же 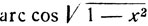 имеем:
имеем:
Отсюда видно, что при отрицательных значениях х написанное выше равенство выполняться не может, так как дуги arc sin х и 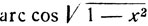 расположены в различных промежутках. В самом деле, при отрицательных значениях х дуга arc sin x заключена в I отрицательной четверти, дуга
расположены в различных промежутках. В самом деле, при отрицательных значениях х дуга arc sin x заключена в I отрицательной четверти, дуга 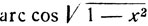 заключена в 1 четверти, так как аргумент арккосинуса есть арифметический корень
заключена в 1 четверти, так как аргумент арккосинуса есть арифметический корень 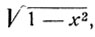 , т. е. число положительное.
, т. е. число положительное.
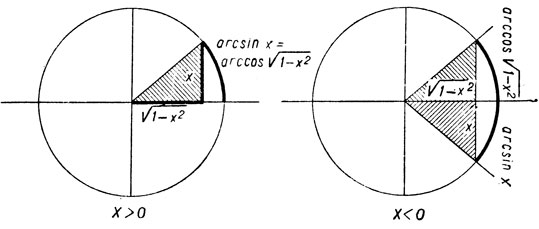
Черт. 33
Расположение рассматриваемых дуг пояснено на чертеже 33.
При отрицательных значениях х имеем: х<0, откуда -x>0 и
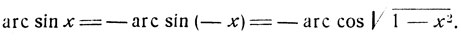
Таким образом, имеем окончательно:
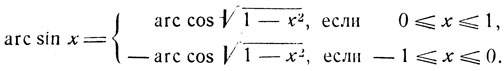
(5)
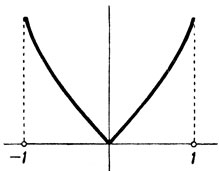
Черт. 34
На чертеже 34 представлен график функции 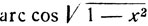 . Область определения есть сегмент [- 1, 1], согласно равенству (5) закон соответствия может быть выражен следующим образом:
. Область определения есть сегмент [- 1, 1], согласно равенству (5) закон соответствия может быть выражен следующим образом:
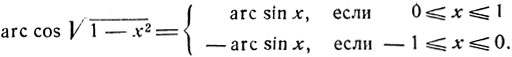
Аналогичными рассуждениями легко показать, что при х≤0 имеем
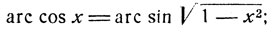
если же -1≤x≤0, то
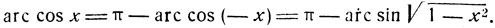
Таким образом:
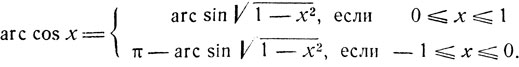
(6)
Переходим к следующему примеру. Из соотношения
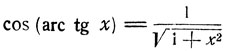
при x≤0 имеем:
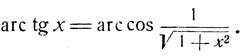
Если же х<0, то
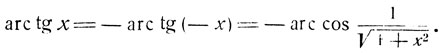
Итак,
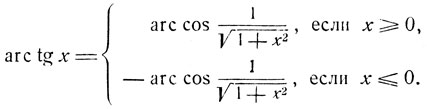
(7)
Аналогично, если 0<х≤1, то 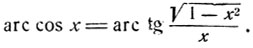
При -1≤x≤0 имеем:
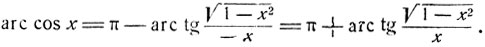
Итак,
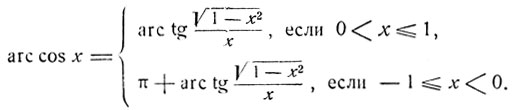
(8)
Следуя методу, выясненному на приведенных примерах, установим справедливость следующих равенств:
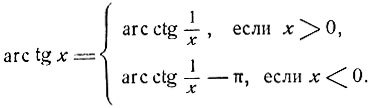
(9)
[при х>0 равенство (9) легко установить; если же х<0, то 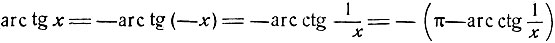 ]
]
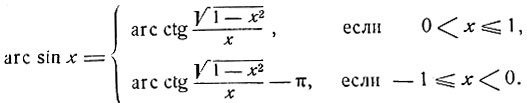
(10)
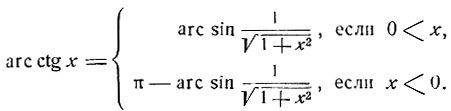
(11)
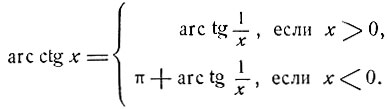
(12)
Примеры:
1) Исследовать функцию y = arc tg x - arc ctg 1/x.
Эта функция определена для всех значений х, за исключением значения х = 0 (при х = 0 второе слагаемое теряет смысл). Воспользовавшись формулами (9), получим:
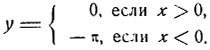
На чертеже 35 изображен график данной функции.
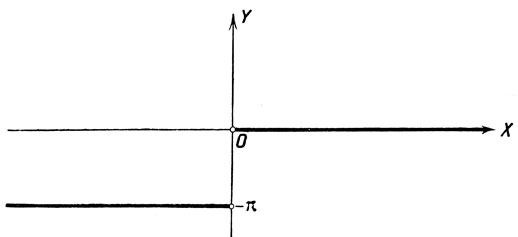
Черт. 35
2) Исследовать функцию 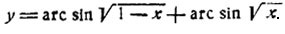
Первое слагаемое определено для значений 0≤x≤1, второе - для тех же значений аргумента. Преобразуем первое слагаемое по формуле (5). Так как 0≤√(1-x)≤1, то получим
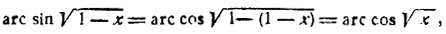
откуда
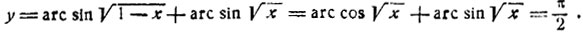
Это равенство выполняется тождественно при всех значениях х на сегменте [0, 1]. Исследуемая функция изображена графически на чертеже 36.
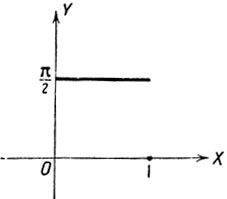
Черт. 36
3) Исследовать функцию
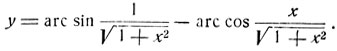
Выражения, стоящие под знаками аркфункции, не превосходят по абсолютной величине единицы, поэтому данная функция определена для всех значений х. Преобразуем первое слагаемое по формуле (5):
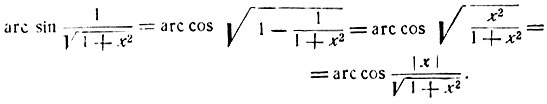
Заметим, что 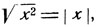 ибо значение корня предполагается арифметическим.
ибо значение корня предполагается арифметическим.
Далее, принимая во внимание равенство:
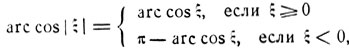
получим:
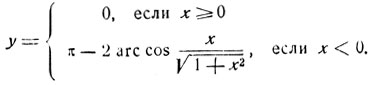
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'